Category: Uncategorized

The Clausius-Clapeyron equation describes how the vapour pressure of a pure substance changes with temperature during a phase change. It has the form

where

is the vapour pressure,
is the enthalpy of vaporisation or enthalpy of sublimation,
is the universal gas constant,
is the temperature in Kelvin,

We can derive the Clausius-Clapeyron equation from the van’t Hoff equation , where for phase transitions such as or , the activity of the pure liquid or solid phase in the equilibrium constant is taken as 1. This simplifies the expression and leads to eq 26.

 

Previous article: Effect of catalysts on equilibria

Content page of chemical equilibrium

Content page of intermediate chemistry

Main content page

Answer to Q1

Let’s label the circuit as follows:

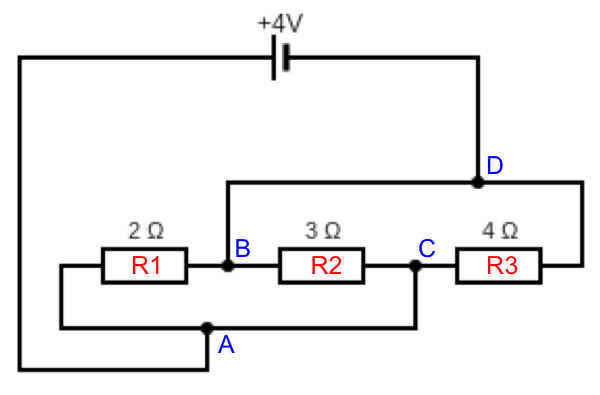
The above circuit can be redrawn as:

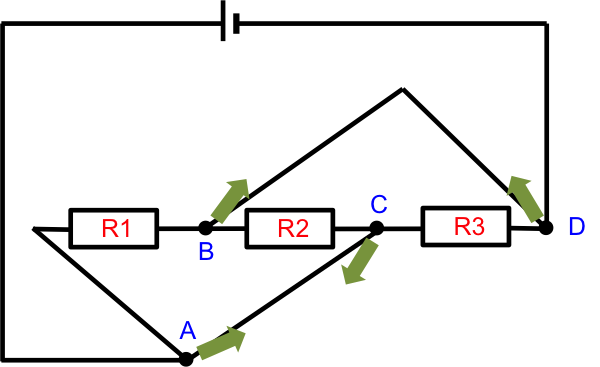
Since junctions A and C have the same potential, we can simplify the diagram by combining them into a single junction (imagine stretching and pulling points A and C towards each other and merging them into one junction). Similarly, junctions B and D have the same potential and can be combined into a single junction. The resultant circuit looks like this:

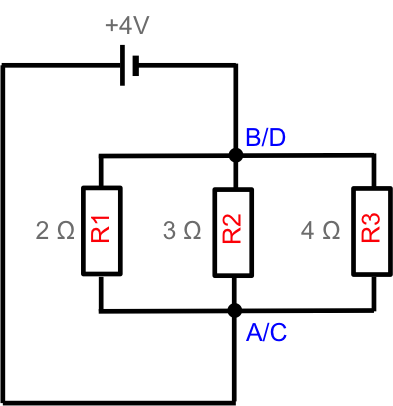
It is a simple circuit with three parallel resistors of effective resistance . The current flowing in the circuit is therefore .

 

Content page of instagram answers

Main content page