- Mono Mole - Page 55

December 13, 2018September 26, 2024

Structure factor (crystallography)

The structure factor, F, is a function that expresses the sum of amplitudes of scattered X-rays from all atoms in a crystal.

We have, in the previous section, discussed the scattering factor of a single atom, which is the sum of amplitudes of waves scattered by the electrons in the atom. We shall now describe the sum of amplitudes of scattered X-rays from all atoms in a unit cell.

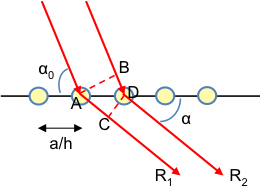
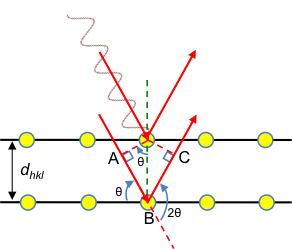
Consider a one-dimensional lattice along the a-axis consisting of two types of atoms (see diagram above). If the Laue equation along the a-axis is satisfied for R₁ and R₃ as well as for R₂and R₄, we have:

$\delta _{11\: atoms}=\delta _{22\: atoms}=\frac{a}{h}(cos\alpha -cos\alpha _0)=n\lambda$

However, if the Laue equation along the -axis is not satisfied for R₁ and R₂ (or for R₂and R₃) we have:

$\delta _{12\: atoms}=x(cos\alpha -cos\alpha _0)$

Combining the two equations above and letting n = 1,

$\delta _{12\: atoms}=\frac{\lambda hx}{a}\; \; \; \; \; \; \; (34)$

Substitute eq28 in eq34,

$\phi =\frac{2\pi hx}{a}\; \; \; \; \; \; \; (35)$

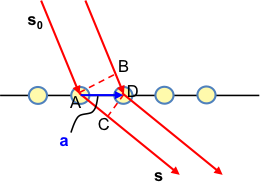
Recall from the previous section that the amplitude of the scattered X-ray received by the detector from an atom is equivalent to the scattering factor $f=4\pi \int_{0}^{\infty }\rho \frac{sinkr}{kr}r^2dr$ . If we have two atoms, the resultant amplitude F at the detector is

$F=f_1+f_2e^{i\phi }\; \; \; \; \; \; \; (36)$

The second term in eq36 includes the factor e^iΦ as the scattered rays from the second atom may have a phase difference from that from the first atom. If Φ = 0, F = f₁+ f₂ .

Question

Show that the intensity detected from eq36 is consistent with the intensity associated to the resultant amplitude of two general complex waves having a phase difference of Φ.

Answer

Let the waves be y₁ = Ae^i(kx-ωt)and y₂ = Be^i(kx-ωt+Φ) . The resultant amplitude is y = Ae^i(kx-ωt)+ y₂ = Be^i(kx-ωt+Φ). As we know, the intensity of the resultant wave is proportional to the square of magnitude of the amplitude of the wave:

$I\propto\left | y \right |^2=y^*y=\left [ Ae^{-i(kx-\omega t)}+Be^{-i(kx-\omega t+\phi )} \right ]\left [ Ae^{i(kx-\omega t)}+Be^{i(kx-\omega t+\phi )} \right ]$

$I\propto A^2+ABe^{i\phi }+ABe^{-i\phi}+B^2$

Since $e^{\pm i\phi}=cos\phi \pm isin\phi$

$I\propto A^2+B^2+2ABcos\phi$

Similarly, for eq36

$I \propto (f_1+f_2e^{-i\phi})(f_1+f_2e^{i\phi})$

$I\propto {f_{1}}^{2}+{f_{2}}^{2}+2 {f_{1}}{f_{2}}cos\phi$

Substitute eq35 in eq36,

$F=f_1+f_2e^{i\frac{2\pi hx}{a}}\; \; \; \; \; \; \; (37)$

In three dimensions, eq37 becomes

$F_{hkl}=f_1+f_2e^{i\frac{2\pi hx_2}{a}}+...+f_je^{i\frac{2\pi hx_j}{a}}+$

$f_1e^{i\frac{2\pi hy_1}{a}}+f_2e^{i\frac{2\pi hy_2}{a}}+ ...+f_je^{i\frac{2\pi hy_j}{a}}+$

$f_1e^{i\frac{2\pi hz_1}{a}}+f_2e^{i\frac{2\pi hz_2}{a}}+ ...+f_je^{i\frac{2\pi hz_j}{a}}$

So,

$F_{hkl}=\sum_{j}f_je^{i2\pi (\frac{hx_j}{a}+\frac{ky_j}{b}+\frac{lz_j}{c})}\; \; \; \; \; \; \; (38)$

The first term in eq38 is $f_1e^{i\frac{2\pi hx_1}{a}}$ in one-dimension. Since there is no phase difference between the resultant X-ray of the first atom with itself, $f_1e^{i\frac{2\pi hx_1}{a}}=f_1$ and eq38 is consistent with eq37, i.e. the phases of scattered X-rays of atoms are relative to that of the first atom at the coordinate of x₁ = 0. Eq38 can be rewritten in terms of fractional coordinates:

$F_{hkl}=\sum_{j}f_je^{i2\pi ({hx_j}'+{ky_j}'+{lz_j}')}\; \; \; \; \; \; \; (39)$

where ${x_j}'=\frac{x_j}{a}$ (i.e. x_jin units of a), ${y_j}'=\frac{y_j}{b}$ , ${z_j}'=\frac{z_j}{c}$ .

The intensity of a diffraction signal is proportional to the square of the magnitude of the three-dimensional structure factor, i.e. $I \propto \left | F_{hkl} \right |^2$ and therefore systematic absences appear when $F_{hkl}=0$ .

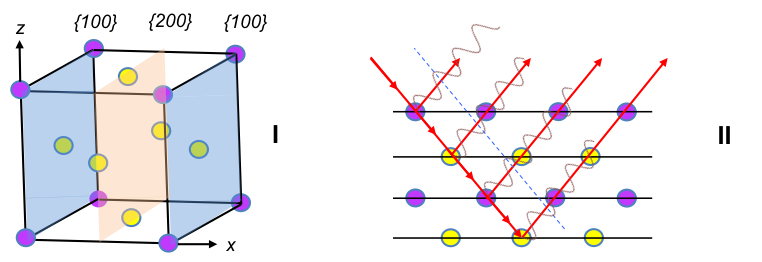
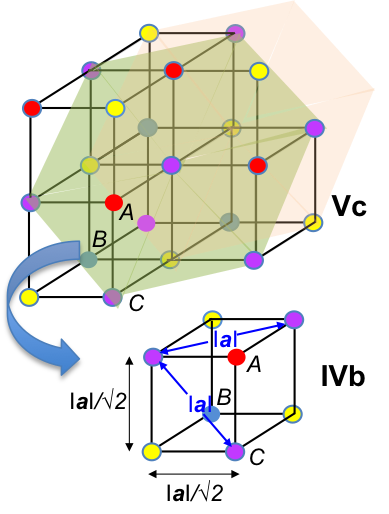
For example, the body centred cubic unit cell (where a = b = c) has fractional coordinates shown in the diagram below.

As the unit cell is composed of the same atoms, the structure factor for each atom is the same. If an atom is shared by m neighbouring unit cells, we multiply the scattering factor of the atom with 1/m. Therefore, eq39 becomes:

$F_{hkl}=\frac{1}{8}f[e^{i2\pi (0+0+0)}+e^{i2\pi (0+k+0)}+e^{i2\pi (h+k+0)}+e^{i2\pi (h+0+0)}+$

$e^{i2\pi (0+0+l)}+e^{i2\pi (0+k+l)}+e^{i2\pi (h+k+l)}+e^{i2\pi (h+0+l)}]+fe^{i2\pi (\frac{h}{2}+\frac{k}{2}+\frac{l}{2})}$

Since e^i2π = cos2π + isin2π = 1, e^iπ = cosπ + isinπ = -1 and e^ab = (e^a)^b

$F_{hkl}=\frac{1}{8}f[1+1^k+1^{h+k}+1^h+1^l+1^{k+l}+1^{h+k+l}+1^{h+l}]+f(-1^{h+k+l})$

Since 1^a = 1

$F_{hkl}=f[1+(-1^{h+k+l})]$

If h + k + l is even, F_hkl = 2f. If h + k + l is odd, F_hkl = 0. Hence, systematic absences occur when h + k + l is odd. A primitive cubic unit cell is different from a BCC in that it does not have an atom at $(\frac{1}{2},\frac{1}{2},\frac{1}{2})$ . Its structure factor is F_hkl = f, which means the diffraction intensities of a cubic P cell has no restriction other than the scattering factor of the atom, which is dependent on the Bragg’s angle θ and hence Bragg’s law of $sin\theta =\frac{\lambda \sqrt{h^2+k^2+l^2}}{2a}$ .

For a face-centred cubic unit cell, the coordinates of the atoms are the same as a cubic P unit cell plus six other atoms on the six faces: $(\frac{1}{2},\frac{1}{2},0)$ , $(\frac{1}{2},0,\frac{1}{2})$ , $(0,\frac{1}{2},\frac{1}{2})$ , $(\frac{1}{2},\frac{1}{2},1)$ , $(\frac{1}{2},1,\frac{1}{2})$ , $(1,\frac{1}{2},\frac{1}{2})$ . These atoms are each shared by two neighbouring cells. The structure factor of a face-centred cubic unit cell is:

$F_{hkl}=f+\frac{1}{2}f[e^{i2\pi (\frac{h}{2}+\frac{k}{2}+0)}+e^{i2\pi (\frac{h}{2}+0+\frac{l}{2})}+e^{i2\pi (0+\frac{k}{2}+\frac{l}{2})}+$

$e^{i2\pi (\frac{h}{2}+\frac{k}{2}+l)}+e^{i2\pi (\frac{h}{2}+k+\frac{l}{2})}+e^{i2\pi (h+\frac{k}{2}+\frac{l}{2})}]$

$F_{hkl}=f+\frac{1}{2}f[(-1^{h+k})+(-1^{h+l})+(-1^{k+l})+(-1^{h+k+2l})+$

$(-1^{h+2k+l})+(-1^{2h+k+l})]$

$F_{hkl}=f+\frac{1}{2}f[(-1^{h+k})+(-1^{h+l})+(-1^{k+l})+(-1^{h+k})(-1^{2l})+$

$(-1^{h+l})(-1^{2k})+(-1^{k+l})(-1^{2h})]$

$F_{hkl}=f+f[(-1^{h+k})+(-1^{h+l})+(-1^{k+l})]$

If h, k, l are all even or all odd, F_hkl = 4f. If one index is odd and two are even, or vice versa, F_hkl = 0. Therefore, a face-centred cubic unit cell does not have systematic absences when h, k, l are all even or all odd.

next article: electron density

previous article: scattering factor

Content page of X-ray crystallography

Content page of advanced chemistry

Main content page

December 13, 2018October 27, 2024

Laue equations

The Laue equations are formulated in 1914 by Max Theodor Felix Laue, a German physicist. Like the Bragg equation, they serve to explain X-ray diffraction patterns.

Consider a one-dimensional row of equally spaced lattice points of a crystal in the diagram above. If $\alpha _0\neq \alpha$ , the path difference δ between R₁ and R₂is given by

$\delta =AC-BD$

Since $AC=\frac{a}{h}cos\alpha$ and $BD=\frac{a}{h}cos\alpha _0$ ,

$\delta =\frac{a}{h}(cos\alpha -cos\alpha _0)$

For constructive interference to occur, the path difference must be an integral multiple of the wavelength of the X-ray radiation. So,

$a(cos\alpha -cos\alpha _0)=nh\lambda\; \; \; \; \; \; \; (15)$

Similarly, for the other two axes of the crystal, we have:

$b(cos\beta -cos\beta _0)=nk\lambda\; \; \; \; \; \; \; (16)$

$c(cos\gamma -cos\gamma _0)=nl\lambda\; \; \; \; \; \; \; (17)$

Eq15, eq16 and eq17 are collectively known as the Laue equations. For constructive interference to occur in three dimensions, the three equations must be simultaneously satisfied.

The Laue equations can also be expressed in vector form (see above diagram), where s and s₀are wave vectors of the scattered and incident X-rays respectively; a is the lattice vector along the a-axis. Again,

$\delta =AC-BD$

Since $AC=\left | \textbf{\textit{a}}\right |cosDAC$ and $\textbf{\textit{a}}\cdot\textbf{\textit{s}}=\left | \textbf{\textit{a}}\right |\left | \textbf{\textit{s}}\right |cosDAC$ , $AC=\textbf{\textit{a}}\cdot \frac{\textbf{\textit{s}}}{\left | \textbf{\textit{s}} \right |}$ . Similarly, $BD=\textbf{\textit{a}}\cdot \frac{\textbf{\textit{s}}_0}{\left | \textbf{\textit{s}} _0\right |}$ . So,

$\delta=\textbf{\textit{a}}\cdot \frac{\textbf{\textit{s}}}{\left | \textbf{\textit{s}} \right |}-\textbf{\textit{a}}\cdot \frac{\textbf{\textit{s}}_0}{\left | \textbf{\textit{s}}_0 \right |}\; \; \; \; \; \; \; (18)$

Substituting $\left | \textbf{\textit{s}}\right |=\left | \textbf{\textit{s}}_0\right |=\frac{1}{\lambda }$ (see below for explanation) in eq18,

$\delta =\lambda\textbf{\textit{a}}\cdot (\textbf{\textit{s}}-\textbf{\textit{s}}_0)\; \; \; \; \; \; \; (19)$

For constructive interference to occur,

$\lambda\textbf{\textit{a}}\cdot (\textbf{\textit{s}}-\textbf{\textit{s}}_0)=h\lambda\; \; \; \Rightarrow \; \; \; \textbf{\textit{a}}\cdot (\textbf{\textit{s}}-\textbf{\textit{s}}_0)=h\; \; \; \; \; where\; h\in \mathbb{Z}\; \; \; \; \; \; \; (20)$

Similarly, for the other two axes, we have,

$\textbf{\textit{b}}\cdot (\textbf{\textit{s}}-\textbf{\textit{s}}_0)=k\; \; \; \; \; where\; k\in \mathbb{Z}\; \; \; \; \; \; \; (21)$

$\textbf{\textit{c}}\cdot (\textbf{\textit{s}}-\textbf{\textit{s}}_0)=l\; \; \; \; \; where\; l\in \mathbb{Z}\; \; \; \; \; \; \; (22)$

Eq20, eq21 and eq22 are the Laue equations in vector form.

Question

Why is $\left | \textbf{\textit{s}}\right |=\left | \textbf{\textit{s}}_0\right |=\frac{1}{\lambda }$ ?

Answer

A wave vector k, like any vector, has a direction and magnitude. Its direction is perpendicular to the wavefront, while its magnitude is defined as the number of waves per unit distance, which is 1/λ. Therefore, $\left | s \right |=\left | s_0 \right |=\frac{1}{\lambda}$ .

Wave vectors and have origins in the de Broglie relation, which is p = h/λ = hk where k = 1/λ. Since p is a vector, k must also be a vector, as h is a constant, i.e. p = hk. This implies that k is also a momentum vector with magnitude of 1/λ.

$\left | \textbf{\textit{k}}\right |=\sqrt{\textbf{\textit{k}} \cdot\textbf{\textit{k}}}=\frac{1}{\lambda }$

next article: equivalence of the laue equations and the bragg equation

Previous article: systematic absences