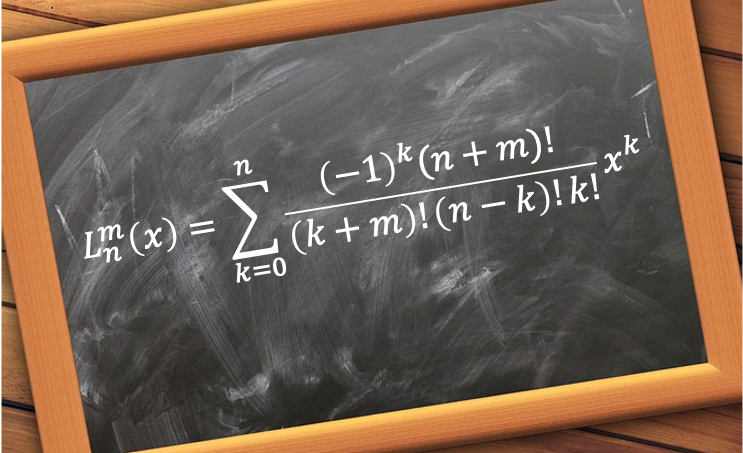gary_mail@hotmail.com

September 23, 2024

Laguerre polynomials

Laguerre polynomials $v(x)$ are a sequence of polynomials that are solutions to the Laguerre differential equation:

$x\frac{d^2v}{dx^2}+(1-x)\frac{dv}{dx}+nv=0\;\;\;\;\;\;\;\;420$

where $n$ is a constant.

When $x=0$ , eq420 simplifies to $\frac{dv}{dx}+nv=0$ . The solution to this first-order differential equation is $v(x)=Ae^{-nx}$ , which can be expressed as the Taylor series $v(x)=A\sum_{n=0}^{\infty}\frac{(-nx)^n}{n!}$ . This implies that eq420 has a power series solution around $x=0$ . To determine the exact form of the power series solution to eq420, let $v(x)=\sum_{j=0}^{\infty}a_jx^j$ .

Substituting $v$ , $v'$ and $v''$ in eq420 yields

$x\sum_{j=0}^{\infty}j(j-1)a_jx^{j-2}+(1-x)\sum_{j=0}^{\infty}ja_jx^{j-1}+n\sum_{j=0}^{\infty}a_jx^{j}=0\;\;\;\;\;\;\;\;421$

$\sum_{j=0}^{\infty}j^2a_jx^{j-1}+\sum_{j=0}^{\infty}(n-j)a_jx^{j}=0$

Setting $j=j+1$ in the first sum,

$\sum_{j=-1}^{\infty}(j+1)^2a_{j+1}x^{j}+\sum_{j=0}^{\infty}(n-j)a_jx^{j}=\sum_{j=0}^{\infty}(j+1)^2a_{j+1}x^{j}+\sum_{j=0}^{\infty}(n-j)a_jx^{j}=0$

$\sum_{j=0}^{\infty}\biggr\[(j+1)^2a_{j+1}+(n-j)a_j\biggr\]x^{j}=0\;\;\;\;\;\;\;\;422$

Eq422 is only true if all coefficients of $x$ in is 0 (see this article for explanation). So, $(j+1)^2a_{j+1}+(n-j)a_j=0$ , or equivalently,

$a_{j+1}=\frac{j-n}{(j+1)^2}a_j\;\;\;\;\;\;\;\;423$

Eq423 is a recurrence relation. If we know the value of $a_0$ , we can use the relation to find $a_1,a_2,...$ .

$\boldsymbol{\mathit{j}}$	Recurrence relation
$0$	$a_1=-na_0$
$1$	$a_2=\frac{1-n}{(1+1)^2}a_1=\frac{n(n-1)}{1^22^2}a_0$
$2$	$a_3=\frac{2-n}{(2+1)^2}a_2=-\frac{n(n-1)(n-2)}{1^22^23^2}a_0$
$\vdots$	$\vdots$

Comparing the recurrence relations, we have

$a_k=(-1)^k\frac{n(n-1)(n-2)\cdots (n-k+1)}{1^22^2\cdots k^2}a_0$

$a_k=(-1)^k\frac{n!}{(k!)^2(n-k)!}\;\;\;\;\;\;\;\;424$

where $a_0=1$ by convention (so that $L_n(0)=1$ ).

Letting $k=j$ in eq424 and substituting it in $v(x)=\sum_{j=0}^{n}a_jx^j$ yields the Laguerre polynomials:

$L_n(x)=\sum_{j=0}^{n}(-1)^j\frac{n!}{(j!)^2(n-j)!}x^j\;\;\;\;\;\;\;\;425$

where we have replaced $v(x)$ with $L_n(x)$ .

The first few Laguerre polynomials are:

$L_0(x)=1$

$L_1(x)=-x+1$

$L_2(x)=\frac{1}{2}(x^2-4x+2)$

$L_3(x)=\frac{1}{6}(-x^3+9x^2-18x+6)$

Next article: Rodrigues’ formula for the Laguerre polynomials

Previous article: Normalisation constant of the Spherical harmonics

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

September 23, 2024

Rodrigues’ formula for the Laguerre polynomials

The Rodrigues’ formula for the Laguerre polynomials is a mathematical expression that provides a method to calculate any Laguerre polynomial using differentiation.

It is given by

$L_n(x)=\frac{e^x}{n!}\frac{d^n}{dx^n}(x^ne^{-x})\;\;\;\;\;\;\;\;428$

To prove eq428, we apply Leibniz’ theorem as follows:

$L_n(x)=\frac{e^x}{n!}\sum_{k=0}^n\begin{pmatrix}n\\k\end{pmatrix}\frac{d^kx^n}{dx^k}\frac{d^{n-k}e^{-x}}{dx^{n-k}}$

Substituting $\frac{d^kx^n}{dx^k}=\frac{n!}{(n-k)!}x^{n-k}$ and $\frac{d^{n-k}e^{-x}}{dx^{n-k}}=(-1)^{n-k}e^{-x}$ in the above equation and rearranging yields

$L_n(x)=\sum_{k=0}^n(-1)^{n-k}\frac{n!}{k!(n-k)!(n-k)!}x^{n-k}$

Letting $j=n-k$ , we have $L_n(x)=\sum_{j=0}^{n}(-1)^j\frac{n!}{(j!)^2(n-j)!}x^j$ , which is the expression for the Laguerre polynomials

Question

How do we change the variable in the summation $\sum_{k=0}^{n}$ by letting $j=n-k$ ?

Answer

When $k=0$ , $j=n$ , and when $k=n$ , $j=0$ . So, $\sum_{k=0}^{n}=\sum_{j=n}^{0}$ . Reversing the summation order, $\sum_{k=0}^{n}=\sum_{j=0}^{n}$ .

Next article: Generating function for the Laguerre polynomials

Previous article: Laguerre polynomials