Basic Chemistry - Mono Mole

October 30, 2019November 6, 2022

Gas laws: overview

Gas laws are mathematical expressions that describe the relationships between physical properties of a gas. These properties include pressure, volume, temperature and the amount of substance (number of moles).

The discovery of gas laws at the end of the 18^th century revolutionises our understanding of the behaviour of gases. In subsequent articles, we shall discuss four gas laws, namely, Boyle’s law, Charles’ law, Gay-Lussac’s law and Avogadro’s law, all of which combine to give the Ideal gas law.

next article: boyle’s law

Content page of gas laws

Content page of Basic chemistry

Main content page

October 30, 2019March 25, 2025

Charles’s law

In 1787, many years after Robert Boyle’s discovery, Jacques Charles, a French scientist, who was a balloon enthusiast, tried measuring the volumes of a balloon that was filled with a gas at various temperatures. He noticed that the volume of the balloon increases linearly with the temperature of the gas on the Celsius scale.

A modern version of Charles’ experiment uses a capillary tube immersed in a temperature controlled water bath (see diagram below). Air is trapped between the close-end of the tube and a column of mercury, with the open-end of the tube exposed to the atmosphere. The pressure exerted on the gas is therefore constant as the gas expands with increasing temperature T.

The linear function can be expressed as:

$V=mT+c\; \; \; \; \; \; \; \; 3$

where m is the gradient of the line and c is the intercept the line makes with the vertical axis.

When the experiment is repeated with different gases at standard atmospheric pressure, the plots of V against T always extrapolate to -273.15 ^oC at zero volume (see graph below).

Since c is the volume of the gas at zero degrees Celsius, V₀, we can rewrite eq3 as

$V=mT+V_0\; \; \; \; \; \; \; \; 4$

The gradient of the line is

$m=\frac{V_0-0}{0-(-273.15)}=\frac{V_0}{273.15}\; \; \; \; \; \; \; \; 5$

Substituting eq5 in eq4,

$V=V_0(1+\alpha T)\; \; \; \; \; \; \; \; 6$

where $\alpha=\frac{1}{273.15}$

In 1848, William Thompson (Lord Kelvin), a British scientist, proposed that the state at -273.15^oC is the lowest temperature that could be achieved theoretically and suggested a new temperature scale called the absolute thermometric scale (also known as the Kelvin scale), which is related to the Celsius scale by:

$K=\: ^oC+273.15$

Thomson named the temperature of -273.15^oC: absolute zero (0 Kelvin). A new graph can be plotted (see diagram below) where volume is now directly proportional to temperature in Kelvin, i.e.

$V=k_2T\; \; \; \; \; \; \; \; 7$

where k₂is the proportionality constant.

Eq7 is eventually called Charles’ law, in Jacques Charles’ honour. It states:

The volume of a given mass of gas is directly proportional to its absolute temperature (K) at constant pressure

Since V₁ = k₂T₁ and V₂ = k₂T₂, Charles’ law can also be expressed as

$\frac{V_1}{T_1}=\frac{V_2}{T_2}\; \; \; \; \; \; \; \; 8$

Note that eq6 is also known as Charles’ law but with T in Celsius. However, it is less commonly used than eq7 or eq8.

Question

Whether the V–T graph is plotted using the Celsius scale or the Kelvin scale, it shows that the temperature of -273.15^oC or 0 K corresponds to V = 0, which does not seem possible as the gas would have liquefied (V ≠ 0) before reaching that temperature. How do we explain this?

Answer

The Gay-Lussac experiment is conducted at a relatively low pressure, where the gas is assumed to behave ideally (see this article for details). In reality, a gas exhibits properties that deviate from ideality and requires a different equation for description (see this intermediate level article for details).

next article: Gay-Lussac’s law

Previous article: Boyle’s law

Content page of gas laws

Content page of Basic chemistry

Main content page

October 30, 2019September 24, 2024

Gay-Lussac’s law

Joseph Gay-Lussac, a French scientist, is often credited with the discovery of the pressure-temperature law in the early 1800s even though Guillaume Amontons, another French scientist had conducted a similar experiment earlier on with the same conclusion. Gay-Lussac’s experimental apparatus involves immersing a gas-filled, fixed-volume bulb-like copper container in a temperature controlled water bath. The container is connected to a pressure gauge, which measures the pressure of the gas in the container at various temperatures (see diagram below).

Both Gay-Lussac and Amontons found that the relationship between the pressure of a gas and its temperature in Celsius is linear at constant volume.

$p=mT+c\; \; \; \; \; \; \; \; 9$

where m is the gradient of the function and c is the intercept the function makes with the vertical axis.

Furthermore, the function extrapolates to -273.15^oC at zero pressure regardless of the gas investigated (see graph above). Similar to the way a Celsius-based expression is derived from Jacques Charles’ experimental data, the Celsius-based formula for Gay-Lussac’s experiments is:

$p=p_0(1+\alpha T)\; \; \; \; \; \; \; \; 10$

where p₀is the pressure of the gas at zero degrees Celsius and $\alpha=\frac{1}{273.15}$ .

By changing the units of the horizontal axis from Celsius to Kevin (see diagram above), the relationship between pressure and temperature becomes directly proportional:

$p=k_3T\; \; \; \; \; \; \; \; 11$

where k₃ is the proportionality constant.

Eq11 is known as the Gay-Lussac’s law (or Amontons’ law), which states:

The pressure of a given mass of gas is directly proportional to its absolute temperature (K) at constant volume

Note that eq10 is also called the Gay-Lussac’s law (or Amontons’ law) with T in Celsius. Since p₁ = k₃T₁ and p₂ = k₃T₂, Gay-Lussac’s law can also be expressed as

$\frac{p_1}{T_1}=\frac{p_2}{T_2}\; \; \; \; \; \; \; \; 12$

Gay-Lussac also experimented on other properties of gases and discovered the law of combining volumes, which states:

Volumes of gases that react with one another are in the ratios of small whole numbers at a given pressure and temperature.

For example, two volumes of hydrogen gas react with one volume of oxygen gas to form two volumes of water:

$2H_2(g)+O_2(g)\rightarrow 2H_2O(g)$

next article: Avogadro’s law

Previous article: Charles’s law

Content page of gas laws

Content page of Basic chemistry

Main content page

October 30, 2019September 24, 2024

Avogadro’s law

Amedeo Avogadro, an Italian scientist, analysed Gay-Lussac’s law of combining volumes and hypothesised in 1811 that

Equal volumes of all gases at the same temperature and pressure have the same number of molecules

This became known as Avogadro’s law or Avogadro’s principle. It implies that for a given temperature and pressure, the volume V of a gas is directly proportional to its amount (in moles), n:

$V=k_4n\; \; \; \; \; \; \; \; 12$

where k₄ is the proportionality constant.

Since V₁ = k₄n₁ and V₂ = k₄n₂, Avogadro’s law can also be expressed as

$\frac{V_1}{n_1}=\frac{V_2}{n_2}\; \; \; \; \; \; \; \; 13$

next article: Ideal gas law

Previous article: Gay-Lussac’s law

Content page of gas laws

Content page of Basic chemistry

Main content page

October 30, 2019December 6, 2024

Ideal gas law

The ideal gas law is a mathematical expression that describes the behaviour of an ideal gas.

So far, all the gas laws mentioned in the previous sections work reasonably well when the experiments are done at low pressures (≤ 1 atm), where the following assumptions about gas particles are valid:

1. They are in constant random motion.
2. They are point masses with zero volume.
3. They are very small compared to the space between them, i.e., they are far apart from one another.
4. There is no intermolecular forces of attraction or repulsion between them.
5. No energy is gained or lost during collisions.

Gases that are made up of such particles are called ideal gases. We can therefore mathematically describe the properties of ideal gases by combining Boyle’s law, Charles’ law and Avogadro’s law as follows:

Boyle’s law: $V\propto\frac{1}{p}$

Charles’ law: $V\propto T$

Avogadro’s law: $V\propto n$

Combining the above laws and rearranging,

$V\propto \frac{nT}{p}\; \; \Rightarrow \; \; V=R\frac{nT}{p}\; \; \Rightarrow \; \; pV=nRT\; \; \; \; \; \; \; \; 14$

where n is defined as the number of moles of gas instead of the earlier arbitrary description of amount of gas, and R is the universal gas constant with a value of 8.3145 J K^-1 mol^-1.

Eq14 is called the ideal gas law. Note that the individual laws still apply; for instance, Gay-Lussac’s law is represented by p = k₃T at constant volume for a given mass of gas, where $k_3=\frac{nR}{V}$ .

Since p₁V₁ = n₁RT₁ and p₂V₂ = n₂RT₂, Avogadro’s law can also be expressed as

$\frac{p_1V_1}{n_1T_1}=\frac{p_2V_2}{n_2T_2}\; \; \; \; \; \; \; \; 15$

Eq14 and eq15 are also known as equations of state, as they interrelate a gas’ physical properties, leading to the knowledge of its physical state. Although these two equations work reasonably well at low pressures, where gases behave ideally, they need to be modified to describe the physical state of gases at high pressures or low temperatures. Gases under such non-ideal conditions are called real gases.

Question

The pressure of a gas in a constant-volume vessel containing 4.000 moles of Pentane and 1.000 mole of Hexane at 80.00°C is 146.8 kPa. Find the pressure of the gas at 45.00°C given:

- Boiling point of pentane: 36.00°C
- Boiling point of hexane: 68.00°C
- Volume of 4 moles of liquid pentane and/or 1 mole of liquid hexane is negligible compared to the volume of the vessel

Answer

Assuming gaseous pentane and gaseous hexane behave ideally, and using eq15 yields

$\frac{146.8\times V}{(4.000+1.000)(80.00+273.15)}=\frac{p_2 V}{4.000\times(45.00+273.15)}$

$p_2=105.8\: kPa$

Next article: Partial pressure

Previous article: Avogadro’s law

Content page of gas laws

Content page of Basic chemistry

Main content page

October 22, 2019March 4, 2025

Basic chemical energetics: overview

Chemical energetics, also known as thermochemistry, is the study of the transformation of energy that occurs during a chemical reaction. It focuses on the exchange of energy between a reaction’s system and its surroundings and utilises the theories of chemical thermodynamics and chemical kinetics to measure, explain and predict these energy exchanges.

next article: Endothermic and exothermic reactions

Content page of basic chemical energetics

Content page of Basic chemistry

Main content page

October 22, 2019September 24, 2024

Endothermic and exothermic reactions

Endothermic and exothermic reactions represent two fundamental categories of chemical processes, with endothermic reactions absorbing heat from their surroundings and exothermic reactions releasing heat, fundamentally influencing temperature changes in their environments.

Chemical reactions involve the breaking of bonds in reactants to give transient or intermediate chemical structures, and the formation of bonds within or between these structures to give the products (see diagram below).

For a reaction system that is not isolated from its surroundings, energy is absorbed by the reaction system from the surroundings during the breaking of bonds and is stored as potential energy, which is then released from the reaction system to the surroundings during the formation of bonds. Hence, energy is neither created or destroyed but is changed from one form to another, and flows from the surroundings to the system or vice versa.

Question

Why is energy released when bonds are formed to give products?

Answer

The fact that products are formed from the transient or intermediate chemical structures implies that products are more stable (lower energy) than the transient or intermediate structures (higher energy). Hence, the net energy change (final energy minus initial energy) is negative, i.e. energy is released during the bond formation process. The initial energy in this case is with reference to the transient or immediate structures and not to the reactants.

Potential energy profile diagrams, with the vertical axis representing potential energy and the horizontal axis representing the progress of a reaction, are used to illustrate energy changes during a reaction. The amounts of energy involved in the processes of bond breaking and bond formation do not exactly match. Consider the case of a reaction depicted in the diagram below.

The energy change in the bond breaking process, q₁ = E_i – E_rt (i.e. energy with respect to the intermediate structures minus the energy with respect to the reactants), is positive. The energy change in the bond formation process, q₂ = E_p – E_i (i.e. energy with respect to the products minus the energy with respect to the intermediate structures), is negative. The total change in energy of the reaction is the energy with respect to the products minus the energy with respect to the reactants:

$q_{net}=E_p-E_{rt}\; \; \; \; \; \; \; \; 1$

Substituting q₂ = E_p – E_iand q₁ = E_i – E_rtin eq1

$q_{net}=q_2+q_1\; \; \; \; \; \; \; \; 2$

For the reaction depicted in the above diagram, q_net> 0. In general, a reaction that requires more energy in the process of bond breaking (energy absorbed from surroundings) than in the process of bond formation (energy released to the surroundings), resulting in the system having a net positive energy (net energy absorbed from surroundings), is called an endothermic reaction.

Conversely, a reaction that requires more energy in the process of bond formation (energy released to the surroundings) than in the process of bond breaking (energy absorbed from surroundings), resulting in a system having a net negative energy (net energy released to the surroundings, q_net < 0), is called an exothermic reaction (see diagram below).

next article: The change in enthalpy of a reaction

Previous article: Overview

Content page of basic chemical energetics

Content page of Basic chemistry

Main content page

October 22, 2019September 24, 2024

The change in enthalpy of a reaction

The change in enthalpy of a reaction is the net transfer of heat of the reaction at constant pressure.

As explained in the previous article, we can use eq1 or eq2 to calculate the change in energy of a reaction. It is difficult to measure the absolute potential energies of the products and reactants, E_pand E_rt. It is also hard to separately quantify the heat transferred from the surroundings to the system q₁during the bond breaking process, and the heat transferred from the system to its surroundings q₂during the bond forming process. However, q_net, the net change in energy during the reaction, is easily measured through experiments. Since many chemical reactions occur at constant pressure, the net transfer of heat q_netat constant pressure is denoted by ΔH, which is called the change in enthalpy of the system. Consequently, the potenital energy profile diagrams are replaced with enthalpy diagrams:

which can also be in the form of enthalpy curves:

where E_ais the activation energy of the reaction, i.e. the minimum amount of energy needed for the reactants to form products.

An endothermic reaction is therefore also defined as a reaction where its change of enthalpy is positive and an exothermic reaction is a reaction where its change of enthalpy is negative. An example of an endothermic reaction is the thermal decomposition of calcium carbonate where net energy is absorbed to breakdown the carbonate into the products:

$CaCO_3(s)\; \begin{matrix} \rightarrow \\ heat \end{matrix}\; CaO(s)+CO_2(g)\; \; \; \; \; \; \; \; \Delta H=+ve$

An example of an exothermic reaction is the combustion of methane where net energy is released in the formation of the relatively stable products of carbon dioxide and water:

$CH_4(g)+2O_2(g) \rightarrow CO_2(g)+2H_2O(l)\; \; \; \; \; \; \; \; \Delta H=-ve$

Theoretically, every reaction is reversible to a certain extent. As shown in the diagram below, the reverse reaction (of any reaction) has an equal magnitude of enthalpy change as the forward reaction but with an opposite sign, e.g. the reverse reaction of the combustion of methane is:

$CO_2(g)+2H_2O(l)\rightarrow CH_4(g)+2O_2(g) \; \; \; \; \; \; \; \; \Delta H=+ve$

Note that the activation energy for the reverse reaction is

$E_a\, '=E_a+\left | \Delta H \right |$

next article: Heat capacity and specific heat capacity

Previous article: Endothermic and exothermic reactions

Content page of basic chemical energetics

Content page of Basic chemistry

Main content page

October 22, 2019December 1, 2024

Measuring the change in enthalpy of a reaction

Measuring the change in enthalpy of a chemical reaction provides essential insights into the heat energy absorbed or released during the reaction.

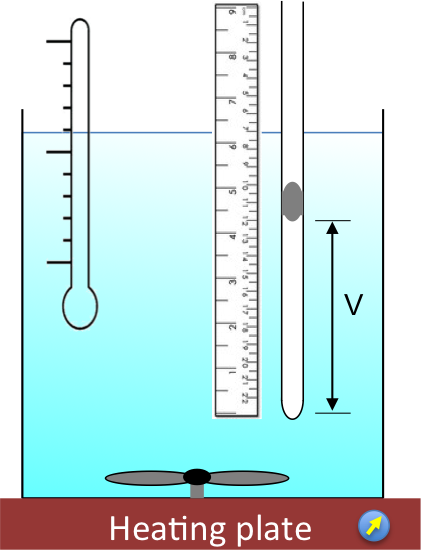
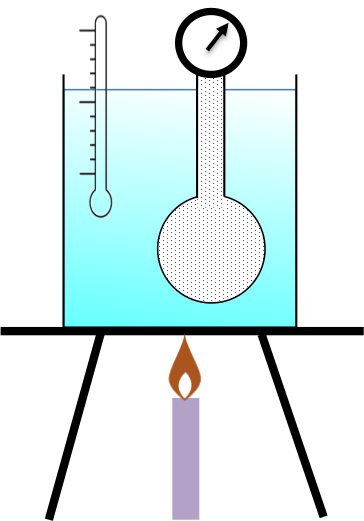
The diagram below shows two devices for measuring enthalpy changes of reactions.

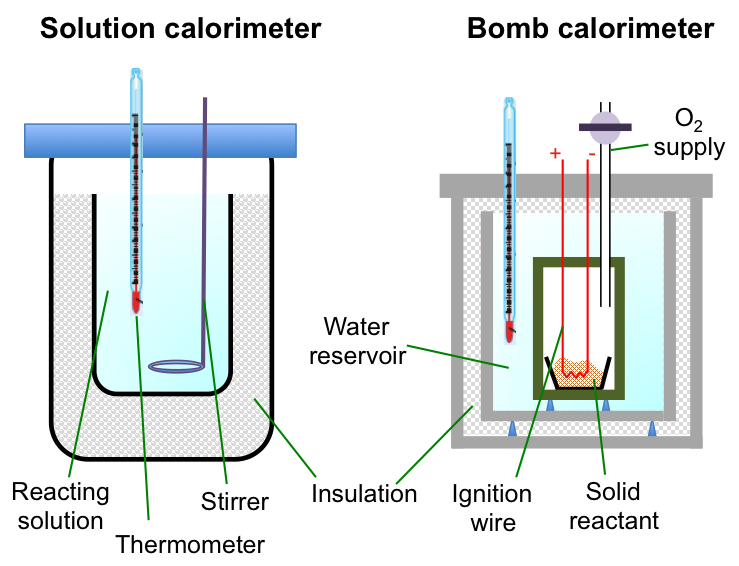
A calorimeter allows the change in temperature of the surroundings of a reaction system to be measured, and hence, the change in enthalpy of the reaction*.

The bomb calorimeter is useful for measuring the change in enthalpy of combustion reactions, e.g.

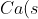$Ca(s)+\frac{1}{2}O_2(g)\rightarrow CaO(s)$

The sample is placed in a crucible enclosed in a chamber made of a thermally conductive material. Oxygen is pumped into the chamber and the reaction is initiated by a current flowing through a wire embedded in the sample. All the energy released by the combustion reaction is assumed to flow across the chamber walls to heat up the water in the reservoir (surroundings). The change in enthalpy of the reaction is calculated by noting the change in temperature of the water reservoir. For example,

Mass of Ca used: 0.001000 kg

Mass of water in the reservoir: 0.4500 kg

Temperature change recorded: 13.10 K

Specific heat capacity of water: 4186 J K^-1 kg^-1

Using eq5, the enthalpy change for the reaction is:

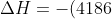$\Delta H=-(4186)(0.4500)(13.10)=-24676\: J\approx-24700\: J$

We have further assumed that heat gained by the chamber walls, and heat lost to the atmosphere, are negligible. The enthalpy change for one mole of calcium is:

$\Delta H=\frac{-24676}{0.001000/0.04010}=-990\: kJmol^{-1}$

Therefore,

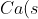$Ca(s)+\frac{1}{2}O_2(g)\rightarrow CaO(s)\; \; \; \; \; \; \; \; \Delta H=-990\: kJmol^{-1}$

It is important to note that the enthalpy change quoted for a reaction changes when we modify the stoichiometric coefficients of the equation. For instance, the quoted ΔH doubles if we rewrite the above equation as:

$2Ca(s)+O_2(g)\rightarrow 2CaO(s)\; \; \; \; \; \; \; \; \Delta H=-1980\: kJmol^{-1}$

In other words, we interpret ΔH = -990 kJmol^-1as the enthalpy change per one mole of calcium or half a mole of oxygen or one mole of calcium oxide for the reaction 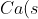$Ca(s)+\frac{1}{2}O_2(g)\rightarrow CaO(s)$ . Similarly, ΔH = -1980 kJmol^-1is the enthalpy change for two moles of calcium or one mole of oxygen or two moles of calcium oxide in the reaction $2Ca(s)+O_2(g)\rightarrow 2CaO(s)$ .

Another perhaps less confusing way to quote the enthalpy change of a reaction is to drop the ‘per mole’ part of the unit to give:

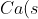$Ca(s)+\frac{1}{2}O_2(g)\rightarrow CaO(s)\; \; \; \; \; \; \; \Delta H=-990\: kJ$

$2Ca(s)+O_2(g)\rightarrow 2CaO(s)\; \; \; \; \; \; \; \Delta H=-1980\: kJ$

We use a solution calorimeter (see above diagram) when we want to measure the enthalpy change of an aqueous reaction, e.g. the neutralisation of hydrochloric acid with sodium hydroxide:

$HCl(aq)+NaOH(aq)\rightarrow NaCl(aq)+H_2O(l)$

Consider the reaction of 20.0 cm³ of 1.000 M HCl with 30.0 cm³ of 1.000 M NaOH resulting in an increase in temperature of 5.46 K. Note that water is considered the surroundings in this experiment, i.e. the reactants are dissolved in their surroundings. There are 0.0200 moles of HCl in 20.0 cm³ of water and 0.0300 moles of NaOH in 30.0 cm³ of water, which means that the total volume of solution is 50.0 cm³. Assuming that the density of the solution is the same as the density of water (1.00 g cm^-3), the mass of the solution is 50.0 g. If we make the further assumption that the specific heat capacity of the solution is the same as that of water (4.18 Jg^-1K^-1), the change in enthalpy of the reaction is:

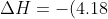$\Delta H=-(4.18)(50.0)(5.46)=-1141\: J\approx-1100\: J$

Since HCl is the limiting reagent, the enthalpy change per mole of H₂O is:

$\Delta H=\frac{-1141}{0.0200}=-57.1\: kJmol^{-1}$

$H^+(aq)+OH^-(aq)\rightarrow H_2O(l)\; \; \; \; \; \; \; \Delta H=-57.1\: kJmol^{-1}$

* The bomb calorimeter actually measures the change in internal energy of the system, which we approximate it to be equal to the change of enthalpy. This is because the system in the bomb calorimeter is a constant-volume environment instead of a constant-pressure environment.

next article: Bond enthalpy

Previous article: Heat capacity and specific heat capacity

Content page of basic chemical energetics

Content page of Basic chemistry

Main content page

October 22, 2019October 3, 2025

Bond enthalpy

The bond enthalpy (also known as bond energy) is the average change in energy required to break one mole of a bond in the gaseous state, e.g. the bond enthalpy for breaking one mole of hydrogen-hydrogen bonds is:

$H_2(g)\rightarrow 2H(g)\; \; \; \; \; \; \; \Delta H_{be}=+436\: kJmol^{-1}$

Bond enthalpies are always positive as reaction systems absorb energy to break bonds.

The reason for including the term ‘average’ in the definition of bond enthalpy is that some bonds, e.g. the carbon-hydrogen bond, are present in different types of molecules:

Methane: H — CH₃

Methanol: H — CH₂OH

Methanoic acid: H — COOH

The bond dissociation energy, which is a specific value and not an average value, for the carbon-hydrogen bond in methane, is different from that in methanol, which is in turn different from that in methanoic acid. This is because the electron density in each carbon-hydrogen bond is influenced by its neighbouring atoms, which are different for each compound. Furthermore, each of the four carbon-hydrogen bonds in methane has a different bond dissociating energy if we were to remove the hydrogen atoms successively, since the electronic environment of the molecule changes from one fragment to another. The table below shows the various bond dissociation energies for one mole of each carbon-hydrogen bond for methane:

Bond	Bond dissociation energy (kJmol^-1)
H — CH₃	435
H — CH₂	444
H — CH	444
H — C	339

Therefore, the average bond dissociation energy for one mole of the carbon-hydrogen bond across a range of compounds is called the bond enthalpy of the carbon-hydrogen bond and is ΔH_be= +413 kJmol^-1. The table below shows bond enthalpies of some common bonds:

Bond	Bond enthalpy, (kJmol^-1)
$H-H$	435
$C-H$	416
$\sigma(C-C)$	348
$C= C$	612
$C\equiv C$	837
$C=O$	743
$\sigma(O-O)$	146
$O=O$	498
$O-H$	460
$Cl-Cl$	243
$H-Br$	366
$Br-Br$	192

Even though bond enthalpy, ΔH_be, is defined as the average change in energy required to break one mole of a bond in the gaseous state, the magnitude of the change in enthalpy to break one mole of a particular bond, $\left | \Delta H_{bb} \right |$ , is the same as the magnitude of the change in enthalpy to form one mole of the same bond, $\left | \Delta H_{bf} \right |$ . Hence, the data in the bond enthalpy table can be used to represent both $\left | \Delta H_{bb} \right |$ and $\left | \Delta H_{bf} \right |$ .

next article: boyle’s law

Question

Answer

next article: Gay-Lussac’s law

Previous article: Boyle’s law

next article: Avogadro’s law

Previous article: Charles’s law

next article: Ideal gas law

Previous article: Gay-Lussac’s law

Question

Answer

Next article: Partial pressure

Previous article: Avogadro’s law

next article: Endothermic and exothermic reactions

Question

Answer

next article: The change in enthalpy of a reaction

Previous article: Overview

next article: Heat capacity and specific heat capacity

Previous article: Endothermic and exothermic reactions

next article: Bond enthalpy

Previous article: Heat capacity and specific heat capacity

next article: Using bond enthalpies to Calculate the change in enthalpy of reactions

Previous article: Measuring the change in enthalpy of a reaction