Category: Basic Chemistry

Posted on

Atomic theory

In 1807, John Dalton, an English Chemist, introduced the atomic theory, which states that all elements are composed of indivisible atoms. He arrived at this conclusion by analysing the data of different chemical reactions, in particular, the proportion by weight in which chemical reactants combined to form products. As many of Dalton’s postulates are flawed (e.g. the thought that atoms are indivisible), the atomic theory is revised over the years to include findings from newer experiments.

In the mid-1800s, the field of electrolysis saw a flourish of experiments. Many scientists, including Michael Faraday, made contributions that suggested the atom is not indivisible, but rather composed of smaller particles. In 1897, J. J. Thomson built one of the earliest mass spectrometers. He discovered a sub-atomic particle, now known as the electron, which has a mass 1700 times smaller than that of a hydrogen ion. Thomson is widely recognised for this significant discovery. Since atoms were known to be electrically neutral, Thomson conjectured that atoms must also be composed of positively charged matter of magnitude equal to the electrons’ negative charge.

In the early 1900s, Earnest Rutherford conducted the Rutherford gold foil experiment, where a beam of He2+ ions (also known as \alpha-particles) were directed at a thin gold foil with the angular distribution of the particles recorded by a counter (see Fig I).

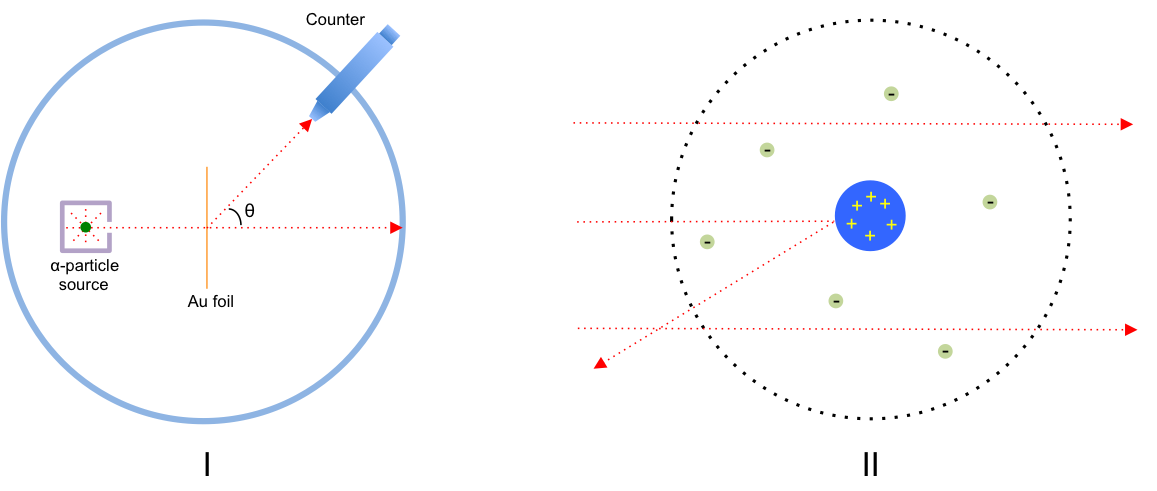
The results revealed that while most of the \alpha-particles passed straight through the gold foil, some were deflected at various angles of up to 1800, suggesting a strong repulsive force by positively charged matter within each gold atom. Rutherford knew from his calculations that if the positively charged matter were diffuse (i.e. distributed throughout the gold atom), its electric field would not be strong enough to deflect the \alpha-particles. That led him to deduce that the positively charged matter must be concentrated in a small region of space in the gold atom. He proposed a model where an atom is composed of a dense and positively charged region in its center, surrounded by orbiting electrons (Fig II). Rutherford further proposed, after reviewing other scientists’ experiments, that the positively charged matter is composed of positively charged sub-atomic particles, which he called: protons.

Rutherford knew that his model was incomplete as the positively charged protons would repel each other apart if they were not held together by some other matter. Years later, he collaborated with Niels Bohr, a Danish physicist, and suggested that the protons in the center of an atom are held together by electrically neutral sub-atomic particles called neutrons. The existence of neutrons was eventually proven by James Chadwick, a British physicist, in 1932 and the combined mass of protons and neutrons is known as the nucleus of an atom.

We now know that protons and neutrons are composed of even more fundamental particles called quarks, which are in turn made of vibrating strings of energy.

 

Question

How did Chadwick discover neutrons and how do they prevent protons from repelling each other apart?

Answer

Chadwick directed \alpha-particles at beryllium, which emitted an unknown radiation that was not influenced by an electric field. The unknown radiation, upon hitting paraffin wax (a hydrocarbon), generated protons (see below diagram). He also found that the unknown radiation consisted of particles, each with mass similar to a proton (see below table), and concluded that they were neutrons.

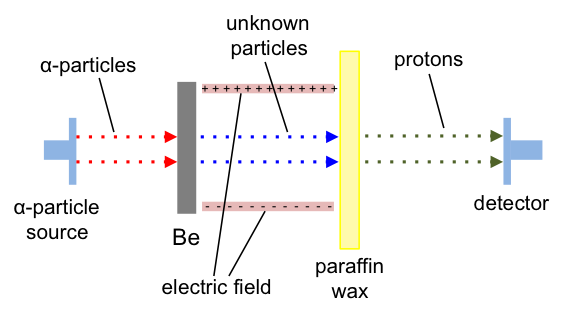
The force binding neutrons and protons in the nucleus is called the nuclear force, which is a residual force of the strong force that binds quarks to form neutrons. Although the nuclear force is a residual force and has a very short range, it is strong enough to bind protons and neutrons together.

 

Particle

 Mass (kg) Relative mass Charge (C)

Relative charge

Proton

 1.673 x 10-27 1 1.673 x 10-27

+1

Neutron

 1.675 x 10-27 1 0

0

Electron

 9.109 x 10-31 \frac{1}{1836} 1.673 x 10-27

-1

 

Next article: Atomic structure: an introduction
Content page of basic quantum chemistry
Content page of Basic chemistry
Main content page
Posted on

Atomic structure: an introduction

Just before Rutherford proposed his model of the atom, Johann Balmer, a Swiss scientist, conducted an experiment to analyse the emission spectrum of hydrogen. This happened in the late 1800s when the wave theory of light was universally accepted by scientists.

The experiment involves using a high potential difference to create an electric spark to split hydrogen gas into atoms in a discharge tube. The excited hydrogen atoms emit a pink radiation, which is separated by a prism into different wavelengths (see diagram below). These spectral lines in the visible range of the electromagnetic spectrum are collectively known as the Balmer series.

Three years after Balmer published his results, Johannes Rydberg, a Swedish physicist developed an empirical formula in 1888 to accurately calculate the wavelengths of spectral lines of the Balmer series for hydrogen. The formula, known as the Rydberg formula, is:

\frac{1}{\lambda}=R_H\left ( \frac{1}{n_1^{\; 2}}-\frac{1}{n_2^{\; 2}} \right )

where λ is the wavelength of a spectral line, RH is the Rydberg constant with the value 1.097 x 107 m-1, and n1 and n2 are integers with n2 > n1.

As the formula was developed empirically, it could not explain why excited hydrogen atoms emitted light of specific wavelengths. Niels Bohr attempted to answer this problem by proposing a new model of the atom with the following postulates:

    1. Electrons can only revolve around the nucleus in stable orbits of certain discrete radii. These orbits are called energy shells.
    2. Orbits further away from the nucleus exist at higher energies. The orbitals are denoted by n = 1,2,3…, with a higher-number orbit being further away from the nucleus.
    3. Electrons gain or lose energy in the form of electromagnetic radiation when they transit between orbits, absorbing energy when they transit from a lower energy orbit to a higher one and emitting energy when they fall from a higher energy orbit to a lower one.

Using the above postulates, Bohr was also able to derive the Rydberg formula theoretically (see this article for details). He explained that when hydrogen gas was split into atoms in Balmer’s experiment, the sole electron in a hydrogen atom was promoted from the n = 1 shell to higher energy shells (n > 2). When the electron fell back down to the n = 2 shell, light of different wavelengths were emitted:

    • 656.3 nm for n = 3 to n = 2, corresponding to red light
    • 486.1 nm for n = 4 to n = 2, corresponding to blue-green light
    • 434.1 nm for n = 5 to n = 2, corresponding to blue-violet light
    • 410.2 nm for n = 6 to n = 2, corresponding to violet light

n1 and n2 in the Rydberg formula now corresponds to energy shells of an electron transition, where n1 refers to the lower energy shell and n2, the higher energy shell.

 

Question

Why doesn’t an excited electron fall back down to the n = 1 shell in the above diagram?

Answer

An excited electron in any of the higher shells of the hydrogen atom (including n = 2) does fall to the n = 1 shell, emitting light in the ultraviolet range of the electromagnetic spectrum. Balmer was only able to detect the emissions in the visible range of the electromagnetic spectrum when he conducted his experiment.

Subsequently, Theodore Lyman, an American physicist, conducted a similar experiment in the early 1900s and discovered the Lyman series, which consists of spectral lines in the ultraviolet range of the electromagnetic spectrum, as a result of electrons falling from higher energy shells to the n = 1 shell. This was followed by discoveries of the Paschen series (n = 3), the Brackett series (n = 4), the Pfund series (n = 5) and the Humphreys series (n = 6) by other scientists.

 

Bohr also suggested that each shell contained a limited number of electrons. For elements heavier than hydrogen, electrons occupy the lower energy shells first. When the limit of electrons in a shell is reached, excess electrons occupy a higher energy shell. Even though Bohr’s derivation of the Rydberg formula was later proven by quantum mechanics to be mathematically sound, his model has certain shortcomings, e.g. according to the model, an electron orbiting around the nucleus would constantly radiate electromagnetic energy and eventually crash into the nucleus. The Bohr model also could not derive the maximum number of electrons for each shell, which was later proven by quantum mechanics to be 2n2 (see below table). Nevertheless, he was awarded the Nobel Prize in Physics in 1922 for his work.

Shell number or principal quantum number (n)

Maximum number of electrons

1

2

2

8

3

18

4

32

 

Question

Calculate the shortest wavelength in the Lyman series.

Answer

The shortest wavelength in the Lyman series corresponds to the radiation with the highest energy, i.e. the transition from the highest shell to n = 1. Substituting n1 = 1 and n2 = ∞ in the Rydberg formula, we have:

\lambda=\frac{1}{R_H}=9.12\times10^{-8}\: m

 

 

Previous article: Atomic theory
Content page of basic quantum chemistry
Content page of Basic chemistry
Main content page
Posted on

Rules for significant figures

In general, a calculated value cannot be more precise than the values used to compute it. The rules regarding significant figures in calculations are as follows:

    • Significant figures of conversion factors and physical constants are not evaluated in determining the precision of the computed result, e.g. 2 moles of an ideal gas occupy 2 x 22.4 = 44.8 dm3 at standard temperature and pressure (2 is the conversion factor).
    • As mentioned, a calculated value cannot be more precise than the values used to compute it. Therefore, when multiplying and dividing numbers, the result usually has the same significant figures as the factor with the least number of significant figures.

For example, 2.1 x 4.01 = 8.421, the result should be rounded off to 2 significant figures, i.e. 8.4. However, if we round off the answer of (25.0 cm3 x 0.100 mol dm3)/28.5 cm3 = 0.0877193 mol dm3 to 3 significant figures, the answer 0.0877 mol dm3, which is a  calculated concentration, will have a precision of 1 in 877, which is more precise than the measured concentration of 0.100 mol dm3, which has a precision of 1 in 100. Therefore, the answer should instead be rounded off to 2 significant figures, i.e. 0.088 mol dm3.

    • When adding and subtracting numbers, the values that are used to compute the result must have the same unit of measurement, e.g. 1.02 g + 2.8216 g + 766.9 g = 770.7416 g. The values 1.02 g, 2.8216 g and 766.2 g, having different decimal places, must be measured using instruments of different precisions, with the instrument giving the last value being the least precise (i.e. a weighing instrument that can only measure values of up to one decimal place). Hence, the result cannot be more precise than 766.2 g and should be reported with one decimal place: 770.7 g. Therefore, when adding and subtracting numbers, the result has the same number of decimal places as the factor with the least number of decimal places.
    • For multi-step calculations, it is a good habit to maintain extra significant figures for answers in the intermediate steps, and only round off the final answer to the appropriate number of significant figures.

 

Previous article: Significant figures
Content page of data treatment
Content page of Basic chemistry
Main content page
Posted on

Significant figures

Significant figures are the number of digits of a number that are known with a certain degree of precision, for example, a burette reading of 15.25 cm3 has 4 significant figures, while the reading of 0.084 g for the mass of an object has 2 significant figures. The rules that determine the number of significant figures in a number are:

    1. Zeros preceding the first non-zero digit of a number are not significant, e.g. 0.084 and 0.1 have 2 and 1 significant figures respectively.
    2. Zeros in between non-zero digits of a number are significant, e.g. 1005 and 1.005 have 4 significant figures each.
    3. Zeros trailing the last non-zero digit of a decimal are significant, e.g. 2.3400 and 0.2300 has 5 and 4 significant figures respectively.
    4. Zeros trailing the last non-zero digit of a positive or negative integer may or may not be significant, e.g. 2500 may have 2 or 3 or 4 significant figures. To avoid confusion, such numbers should be expressed in standard form, e.g. 2.5 x 103, 2.50 x 103 and 2.500 x 103 have 2, 3 and 4 significant figures respectively.

 

 

Next article: rules for Significant figures
Content page of data treatment
Content page of Basic chemistry
Main content page
Posted on

Concentration of a chemical species

The concentration of a chemical species in a solution can be expressed in a few ways, namely,

i) Molar concentration or molarity

The molar concentration, c, of a solute (i.e. a chemical species in a solvent) is defined as

c=\frac{n}{V}

where n is the number of moles of the solute and V is the volume of the solvent. V is usually expressed in units of L, dm3 or cm3, which means that the molar concentration, c, has units of mol L-1, mol dm-3 or mol cm-3, respectively, even though the SI unit for c is mol m-3. As the units mol L-1 and mol dm-3 are equivalent and most commonly used, they are given the symbol M, which is called molar (not to be confused with molar mass, M). For example,

Q:      How many moles of NaCl are there in 250.0 mL of a 0.100 M sodium chloride solution?

A:      n=cV=0.100\times\frac{250.0}{1000}=0.025\, moles

 

ii) Mass concentration

The mass concentration, ρ, of a solute is defined as

\rho=\frac{m}{V}

where m is the mass of the solute in grams and V is the volume of the solvent, usually in dm3 or cm3. For a pure chemical, e.g. water or molten iron, the mass concentration equals its density. A chemical species’ mass concentration can be converted to its molarity by dividing it with its molar mass, M:

\frac{\rho}{M}=\frac{m}{MV}=\frac{n}{V}=c

 

iii) Number concentration

The number concentration (or number density), C, of a solute is defined as

C=cN_A=\frac{nN_A}{V}

where NA is the Avogadro constant. Number concentration is used when the number of particles in a particular volume is countable, e.g. macromolecules.

 

iv) Molality

The molality, b, of a solute is defined as

b=\frac{n}{m_{solvent}}

where msolvent is the mass of the solvent and the units for b is mol kg-1. Molality is sometimes preferred over molarity in measuring the concentration of a chemical species, as the latter varies according to temperature due to thermal expansion.

Previous article: The ionic equation
Content page of Stoichiometry
Content page of Basic chemistry
Main content page
Posted on

The ionic equation

An ionic equation is a simplified version of a chemical equation that involves ions.

The construction of an ionic equation is usually accomplished in three steps, which can be illustrated using the example of the reaction between solid zinc and a solution of sulphuric acid:

Step 1:        Write the full equation

Zn(s)+H_2SO_4(aq)\rightarrow ZnSO_4(aq)+H_2(g)

Step 2:        Rewrite the equation such that the aqueous species are in their dissociated forms

Zn(s)+2H^+(aq)+SO_4^{\; 2-}(aq)\rightarrow Zn^{2+}(aq)+SO_4^{\; 2-}(aq)+H_2(g)

Step 3:        Remove ions that appear on both sides of the equation (such ions are known as spectator ions)

Zn(s)+2H^+(aq)\rightarrow Zn^{2+}(aq)+H_2(g)

The purpose of writing an ionic equation is to highlight the chemical species that are playing an active role in a reaction, which for the above reaction are Zn(s) and H+(aq) for the products, and Zn2+(aq) and H2(g) for the reactants, with SO42-(aq) playing the ‘inactive’ or spectator role.

 

NEXT ARTICLE: Concentration of a chemical species
Previous article: Balancing a chemical equation
Content page of Stoichiometry
Content page of Basic chemistry
Main content page
Posted on

Balancing a chemical equation

The concept of balancing a chemical equation is based on the law of conservation of mass, where the total mass of reactants equals the total mass of products.

For example, the neutralisation reaction of sodium hydroxide with sulphuric acid could be:

NaOH(aq)+H_2SO_4(aq)\rightarrow Na_2SO_4(aq)+H_2O(l)

However, you’ll realise that the number of atoms on the left hand side of the equation is not equal to that on the right, which means that the law of conservation of mass is violated. To balance the equation, we adjust the stoichiometric coefficients to give:

2NaOH(aq)+H_2SO_4(aq)\rightarrow Na_2SO_4(aq)+2H_2O(l)\; \; \; \; \; \; \; \; 1

or

NaOH(aq)+\frac{1}{2}H_2SO_4(aq)\rightarrow \frac{1}{2}Na_2SO_4(aq)+H_2O(l)

Since we usually represent the stoichiometric coefficients as whole numbers, eq1 is preferred.

 

Question

Construct and balance the chemical equation for the complete combustion of 1-heptene.

Answer

First, write a draft equation excluding the stoichiometric coefficients

C_7H_{14}(l)+O_2(g)\rightarrow CO_2(g)+H_2O(l)

Next, balance the equation by focusing on one element at a time. For example, we can start with carbon, followed by hydrogen and then oxygen to give the following equations:

C_7H_{14}(l)+O_2(g)\rightarrow{\color{Red} \mathbf{7}}CO_2(g)+H_2O(l)

C_7H_{14}(l)+O_2(g)\rightarrow{\color{Red} \mathbf{7}}CO_2(g)+{\color{Red} \mathbf{7}}H_2O(l)

C_7H_{14}(l)+{\color{Red} \mathbf{\frac{21}{2}}}O_2(g)\rightarrow{\color{Red} \mathbf{7}}CO_2(g)+{\color{Red} \mathbf{7}}H_2O(l)\; \; \; \; \; \; \; \; 2

Since whole numbers of stoichiometric coefficients are preferred, we multiply both sides of eq2 by 2 to give:

2C_7H_{14}(l)+21O_2(g)\rightarrow 14CO_2(g)+14H_2O(l)

 

NEXT ARTICLE: The ionic EQUATION
Previous article: The chemical equation
Content page of Stoichiometry
Content page of Basic chemistry
Main content page
Posted on

The chemical equation

A chemical equation describes the changes that occur during a chemical reaction. Instead of writing an equation using words, for example:

1 part of solid zinc & 2 parts of hydrochloric acid gives 1 part of zinc chloride & 1 part of hydrogen gas

we express it as:-

1Zn(s)+2HCl(aq)\rightarrow 1ZnCl_2(aq)+1H_2(g)

or simply (by omitting the number 1, which is quite redundant)

Zn(s)+2HCl(aq)\rightarrow ZnCl_2(aq)+H_2(g)

In general, a chemical equation has the form:

where

    1. the upper-case letters represent elements, ionic formula or molecular formula (each entity is known as a chemical species);
    2. the lower-case letters (known as stoichiometric coefficients) represent the relative portions of chemical species in the reaction;
    3. the letters in brackets indicate the physical state of the elements or molecules (s for solid, l for liquid, g for gas and aq for aqueous, i.e. a species dissolved in water); and
    4. a single-arrow or double-arrows symbol is included depending on whether the chemical reaction is non-reversible or reversible respectively.

Note that the ratio of stoichiometric coefficients for the chemical species in the zinc-acid chemical equation above is 1:2:1:1. Hence, we can say that one mole of zinc reacts with two moles of hydrochloric acid to give one mole zinc chloride and one mole hydrogen gas.

 

NEXT ARTICLE: Balancing a CHEMICAL EQUATION
Previous article: Stoichiometry: overview
Content page of Stoichiometry
Content page of Basic chemistry
Main content page
Posted on

Stoichiometry: overview

Stoichiometry is the calculation of the relative amounts of products and reactants in a chemical reaction.

The word stoichiometry comes from the greek words stoicheion, meaning element, and metron, meaning measure. To calculate the amounts of products and reactants in a chemical reaction, we need to first know how to construct and balance a chemical equation.

 

Next article: The chemical equation
Content page of Stoichiometry
Content page of Basic chemistry
Main content page
Posted on

Basic chemical kinetics: overview

Chemical kinetics is the study of the rates of chemical reactions. The analysis of the rates of chemical processes involves understanding how different factors like temperature and pressure affect the speed of these processes, which in turn allow us to optimise conditions to synthesise useful products safely and efficiently.

The rate of a reaction is defined as:

rate=\frac{change\, in\, amount\, of\, reactants\, or\, products}{change\, in\, time}\; \; \; \; \; \; \; \; 1

with the amount of reactants or products being measured by mass, volume or number of moles.

 

Next article: measuring the rate of a reaction
Content page of basic chemical kinetics
Content page of Basic chemistry
Main content page