The first hypothesis, formulating the constitutive relation for an incompressible and viscous Newtonian fluid, states that the stress tensor of a fluid at rest is the pressure exerted by the fluid .
Stress is the measure of the amount of forces exerted by neighbouring particles of a material (e.g. a body of fluid) on one another. In fluid dynamics, stress consists of a hydrostatic portion and a hydrodynamic portion:
The components of stress that are perpendicular to the material’s cross section are simply the pressure exerted by the fluid (hydrostatic), while those that are coplanar with the material’s cross section are called shear stress (hydrodynamic).
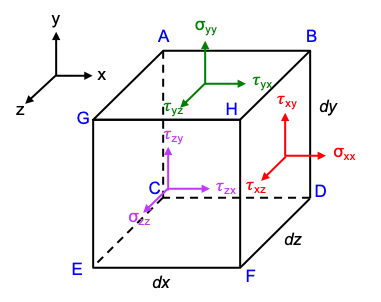
To quantify a component of stress, we need to indicate a magnitude and two directions, one for the surface (surface direction is given by the normal vector to the surface) and the other for the direction of force acting on that surface. We can combine the two directions using a 2-letter subscript, with the first letter indicating the surface direction and the second letter denoting the force direction. For example, τxy is the component of stress with a y-direction force acting on the x-direction surface (i.e., surface BDFH). To further distinguish surface BDFH from surface ACEG, we write the y-direction force on BDFH as τxy(x+dx) and that on ACEG as τxy(x).
Therefore, stress can be mathematically represented by a matrix that has nine components. We call such a matrix, a second-order tensor σij . To differentiate perpendicular components from coplanar components, we denote the former by σij and the latter by τij. The stress tensor can be expressed as:

Question
How do we indicate stress components on the remaining 3 surfaces, i.e. ACEG, CDFE and ABDC?
Answer
Let’s illustrate this with an example. As mentioned above, to distinguish the y-direction force on BDFH from the y-direction force on ACEG, we denote each component as a function of distance, writing the former as τxy(x+dx) and the latter as τxy(x).
Hypothesis 1 states that, when the fluid is at rest:
By convention, pressure is given a negative sign while stress, which is tensile in nature, is afforded a positive sign. Combining eq1 and eq2,
where τij = 0 when the fluid is at rest and δij is the Kronecker delta.
Eq3 in matrix form is,