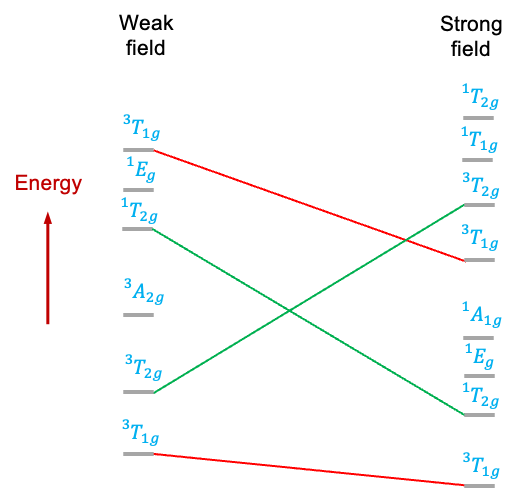
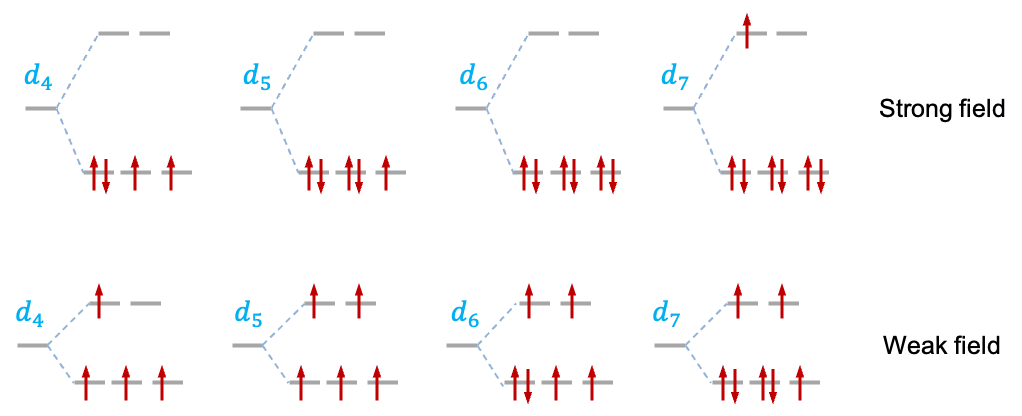
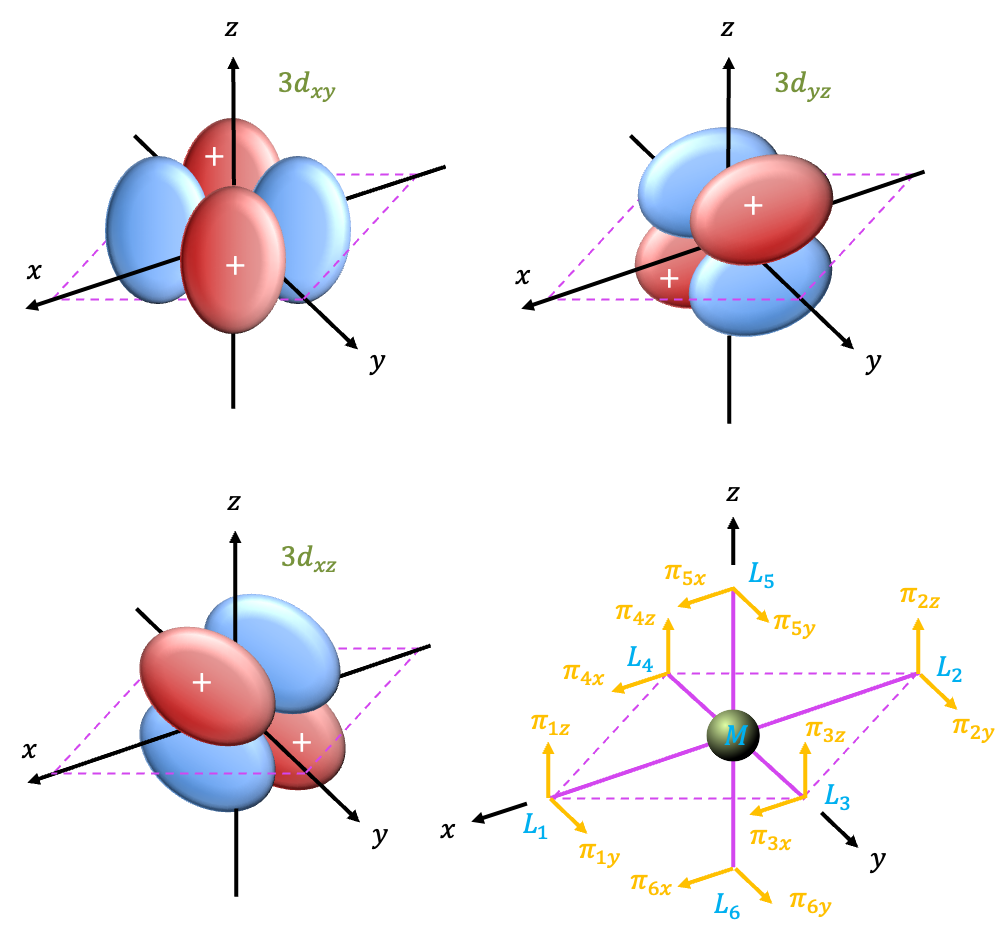
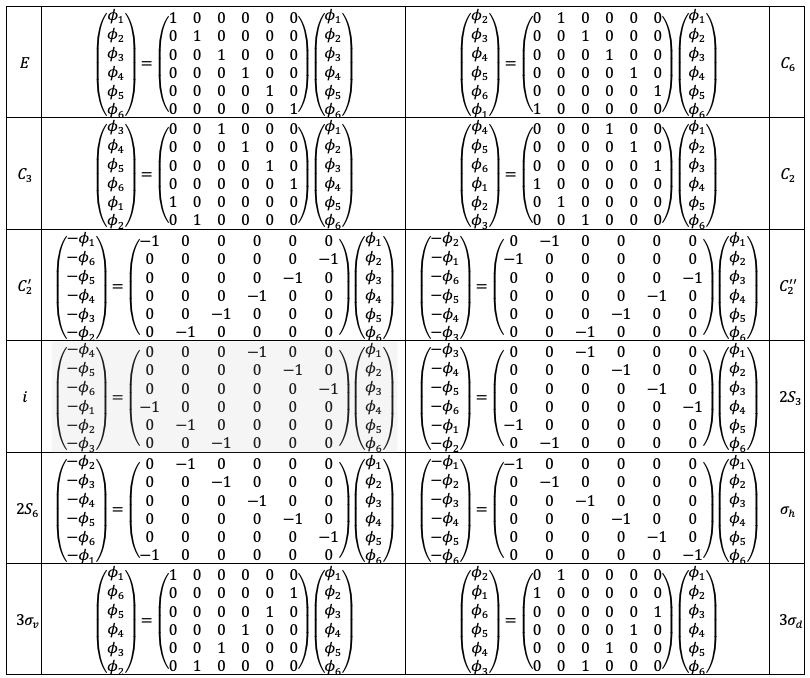
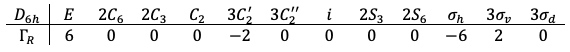A correlation diagram is a graphical representation that shows how the energies of the various states of a free -metal ion change when placed in an octahedral ligand field of varying strength. It is useful for studying
transitions, which are electronic transitions that occur between molecular orbitals (MOs) of
-metal octahedral complexes that are mostly metal in character.
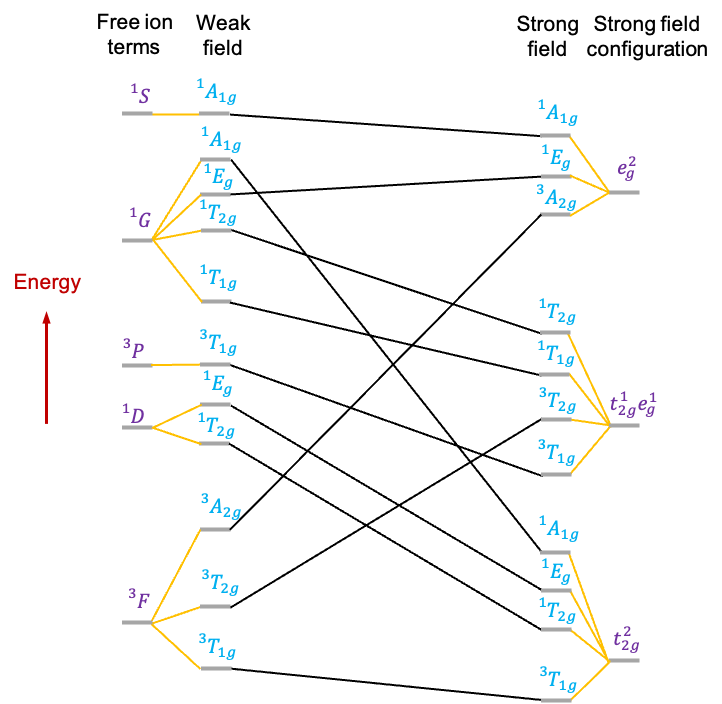
Consider a transition metal ion, such as , with a
electronic configuration. Its correlation diagram (see diagram above) exhibits the following features:
-
- The free metal ion states, represented by atomic term symbols without spin-orbit coupling, are tabulated on the extreme left.
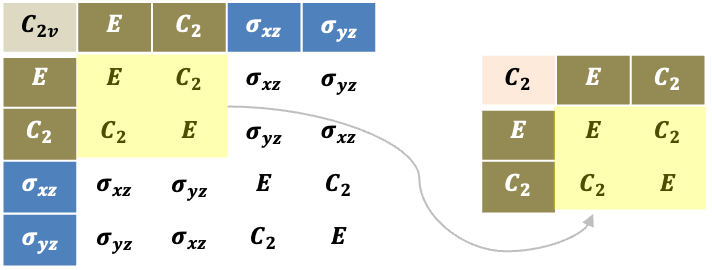
- To the right of the term symbols, we assume that the free metal ion is subject to a weak octahedral ligand field, which is just strong enough to lift the degeneracy of microstates associated with each term symbol. The symmetries of the resulting states of distinct energy are denoted by irreducible representations of the
point group.
- On the extreme right, we list the irreducible representations corresponding to the electronic configurations of the metal ion in a strong octahedral ligand field.
- Additionally, lines connect states of the same symmetry.
The atomic terms () of such a free metal ion are constructed using the Russell Saunders coupling techniques. Each term corresponds to a specific energy level of the
electronic configuration. Within each term, microstates with the same energy are grouped together. Overall, there are 45 microstates distributed across these five terms. The wavefunction for each microstate is the product of two one-electron
-orbital wavefunctions,
, where
, and its corresponding energy comes from the solution of
. Hund’s rules predict that the terms are, in order of increasing energy
and
. However, spectroscopic measurements have shown that the actual order is
and
.
In the presence of a weak octahedral ligand field, the formation of the MOs of the complex is assumed to involve a small perturbation on the energies corresponding to the atomic terms, such that the symmetries of the MOs are characteristic of an octahedral environment. The energies of these MOs are eigenvalues of the Hamiltonian , where
is the unperturbed Hamiltonian and
is the perturbed Hamiltonian due to the weak ligand field. The method to determine the symmetries of microstates involves examining how a one-electron wavefunction of the metal ion behaves under
symmetry operations and then extending the results to
.
A one-electron hydrogenic total wavefunction has the formula , where the spatial function
. Here,
,
, and
represent the radial, angular (spherical harmonics) and spin functions, respectively. Any symmetry transformation of
affects only the angular part of the total wavefunction because the radial and spin functions remain invariant under all symmetry operations of a point group. This implies that the character table of a regular point group is generated solely via spherical harmonics.

Question
Why are the radial and spin functions invariant under all symmetry operations of a point group?
Answer
The radial function is a function of the distance of an electron from the origin. Symmetry operations do not affect
. The spin function describes an intrinsic form of angular momentum of electrons known as spin, which is independent of the spatial coordinate system. However, it is possible to generate character tables that depend on both spatial and spin coordinates. Such point groups are known as double groups. The main difference between a regular point group and a double group lies in the basis functions used to generate them: spherical harmonics for regular point groups and total wavefunctions for double groups. In other words, representations of double groups account for the combined symmetry properties of the full wavefunction, not just the spatial part. The character table of a double group can be perceived as an expansion of the character table of a regular group, with additional representations and classes. We will explore how certain properties of double groups are useful in constructing the correlation diagram of the
electronic configuration.
Let’s analyse the symmetry operations of the point group on
. When the rotation operator
acts on
by an angle
around the
-axis, only the azimuthal angle
is affected and each basis is transformed into
. The transformation for all basis functions is summarised as:
The character of the rotation matrix is , which is a geometric series
, where
,
and
. This implies that
Using Euler’s formula of ,
When ,
. Applying L’Hopital’s rule,
Since the basis functions for the electronic configuration are
-orbitals, which are even with respect to inversion,
An improper rotation combines two symmetry operations: rotation and reflection. A reflection
of the angular function about the plane perpendicular to the rotation axis affects only the polar angle
and transforms it to
. Noting that the explicit expression of the un-normalised spherical harmonics is
, we have
. As
for each basis function,
Therefore,
and
It follows that when ,
Although, the angular momentum quantum number in eq111 through eq115 is associated with a single electron, it can be replaced by the total angular momentum quantum number
in those equations for two reasons. Firstly, the number of degenerate states for both
and
is the same (degenerate states for
and
correspond to distinct values of
and
, respectively). Secondly, a two-electron basis function for an atomic term (e.g. a
term) is given by
, where
,
and
.
is analogous to the one-electron spherical harmonics
.
Consequently, the characters for the reducible representation corresponding to term
, where
, are
| 7 | 1 | -1 | -1 | -1 | 7 | -1 | 1 | -1 | -1 |
can then be decomposed using eq27a into
. The three irreducible representations have the same spin multiplicity as
because the perturbed Hamiltonian only causes a small change in the
microstates’ energies and does not affect their common spin multiplicity. Using the same logic, the reducible representations of
and
decompose to the corresponding terms shown under the weak field column in the correlation diagram above.

Question
For , the constituent irreducible representations have the same spin multiplicity as
. What happens if the constituent representations of a reducible representation corresponding to an electronic configuration are associated with both singlet and triplet microstates?
Answer
As mentioned earlier, is derived using spherical harmonics. When considering the total wavefunction of a microstate, which includes the spin wavefunction, we must search for clues to assign the correct spin multiplicities to the constituent irreducible representations of
. Fortunately, for the weak field case, the atomic terms serve as a reference for assignment. When the free metal ion is subject to a strong ligand field, there are scenarios where the constituent irreducible representations of a reducible representation, for instance
, can correspond to both singlet and triplet microstates (see below for details). In such cases, we form a new representation using total wavefunctions as basis functions. The resultant reducible representation, which belongs to a double group, is enlarged:
.
In the presence of a strong octahedral ligand field, the field’s contribution to the energy of an MO now dominates over the energy due interelectronic repulsion in the ion. The ligand field splitting parameter is large and the only possible configurations are ,
and
. The wavefunction of each of the configurations is assumed to be the product of two one-electron
-orbital wavefunctions. This implies that the symmetries of the three configurations can be derived using the concept of direct product representations. With reference to the character table of the
point group, we have
| 9 | 0 | 1 | 1 | 1 | 9 | 1 | 0 | 1 | 1 | |
| 6 | 0 | 0 | 0 | -2 | 6 | 0 | 0 | -2 | 0 | |
| 4 | 1 | 0 | 0 | 4 | 4 | 0 | 1 | 4 | 0 |
Even though the three representations are direct product representations, their characters are fundamentally linked to eq111 through eq115, which are functions of the total angular momentum of a state. Since the number of microstates are the same under a weak or strong field, both angular and spin momenta of the microstates are preserved. In other words, we would expect the three reducible representations to decompose into irreducible representations that correspond one-to-one with the eleven states in the weak field scenario.
Using eq27a, the reducible representations in the above table decompose to

Question
What is the difference between orbital symmetries and configuration symmetries?
Answer
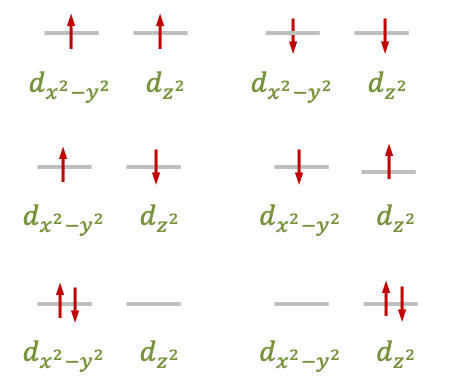
The degenerate and
orbitals are one-electron wavefunctions that transform together according to the
irreducible representation of the
point group. For the case of the
configuration, there are six possible ways to fill these orbitals with two electrons (see diagram below). Each of these six microstates is described by a two-electron wavefunction that is a product of two one-electron
-orbital wavefunctions. These wavefunctions transform according to a reducible representation
, which can be decomposed into the symmetries
and
.
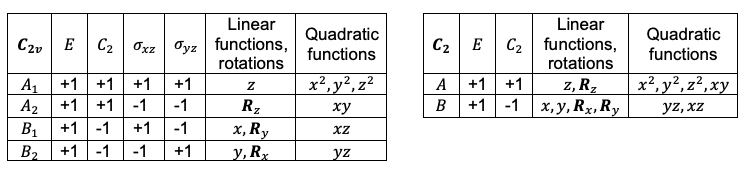
The next step is to determine the spin multiplicities associated with the irreducible representations of each configuration. One approach is to use the descent of symmetry method, as spin multiplicities are intrinsic properties of electrons that remain independent of the system’s symmetry. For this method to be effective, the chosen subgroup must facilitate the mapping of irreducible representations from the parent group to different representations within the subgroup. One subgroup that satisfies this mapping criterion for
is the
point group.
| → | ||
| → | ||
| → |

Question
What does of the
point group correlate to in the
point group? Show that
of the
point group is equivalent to
.
Answer
Using the correlation table above,
of the
point group correlates to
of the
point group. Let
and
be the characters of
and
, respectively.
is equivalent to
as they are related by a similarity transformation. So,
Since
and
,
. Consequently, the relationship between
and
can be described by the diagram below.
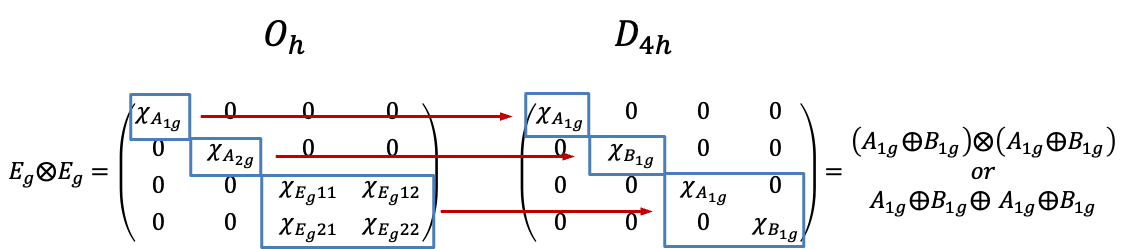
The reducible representations of of
and
of
share the same set of basis functions. Even though these functions are spherical harmonics, their total wavefunctions must be associated with certain spin states. For instance, the basis functions of the
block of
describe either a singlet or triplet spin state, as they are a degenerate pair. The pair also transforms according to the
block of
. To proceed with the determination of the spin multiplicity of wavefunctions that transform according to
, we need to analyse the microstates in the
environment.
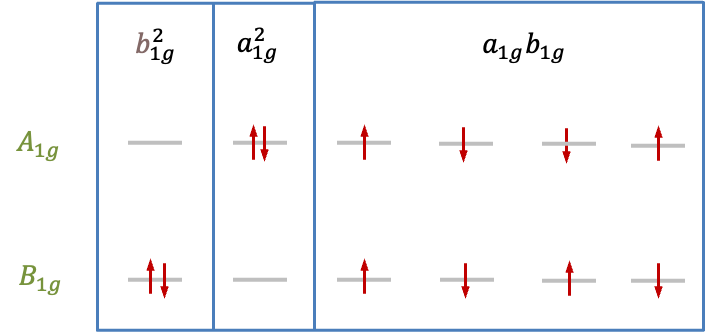
| Microstate analysis
According to the |
|
Configuration |
Direct product |
Spin state |
Symmetry of microstate |
| Singlet | |||
| Singlet, triplet | |||
| Singlet |
Since the wavefunction that transforms according to of the
block represents a singlet, the degenerate pair of wavefunctions corresponding to the
block of
must also describe a singlet state. This implies that the wavefunction that transforms according to
of the
block also represents a singlet. As there are two triplet microstates out of the six microstates in the
environment, the remaining representation
must be associated with triplet wavefunctions. Consequently, the states that arise from the
configuration in the
environment are grouped into
and
, which can be expressed as the double group representation
.

Question
How do we verify that is correct?
Answer
The and
irreducible representations are associated with one and two linearly independent basis functions, respectively. A singlet spin state and a triplet spin state are associated with one and three spin wavefunctions, respectively. Therefore, we can form
microstates for
.
| → | ||
| → | ||
| → | ||
| → |
Repeating the above logic, the subgroup that satisfies the criterion for mapping of
is the
point group. The fifteen microstates of
transform according to the reducible representation
, which correlates to
of
.
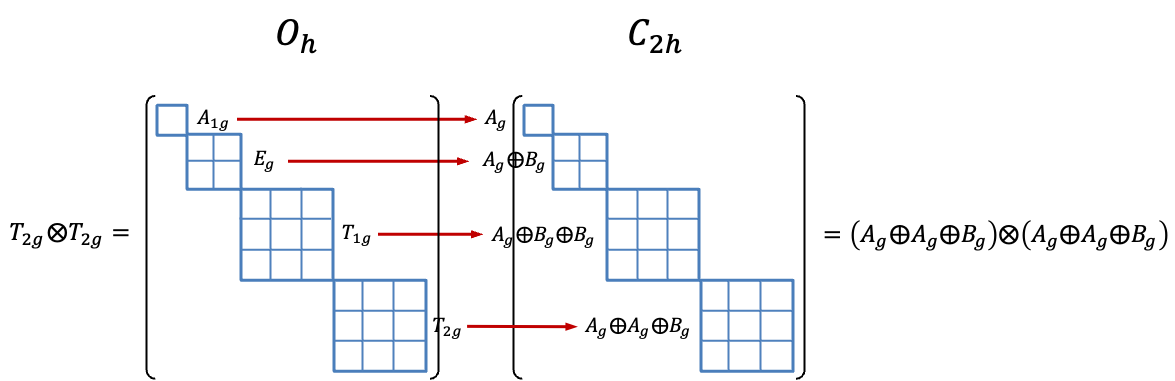
| Microstate analysis
The degeneracy of the |
|
Configuration |
Direct product |
Spin state |
Symmetry of microstate |
| Singlet | |||
| Singlet, triplet | |||
| Singlet, triplet | |||
| Singlet | |||
| Singlet, triplet | |||
| Singlet |
Basis functions that transform according to one of the blocks of must describe either singlet or triplet states. Since there are three triplet microstate symmetries in the
environment, one of which is
, the only possibility is for the wavefunction that transforms according to the
block to represent a triplet, while the wavefunctions belonging to the remaining blocks describe singlets. In other words, the states that arise from the
configuration in the
environment are grouped into
and
. Similarly, we can verify that we have
microstates for
.
The remaining configuration is associated with twenty-four microstates. As the two
-electrons are in different orbitals, their spins may be either paired or unpaired. Without using the descent of symmetry method, it is obvious that the only way to assign the twenty-four microstates is to form the double group representation
.
Finally, we can complete the correlation diagram by connecting the states between the weak and strong fields using the non-crossing rule.