Continuity equation

A continuity equation in fluid mechanics is an equation that makes use of the conservation-of-mass theory to describe the transport of fluid.

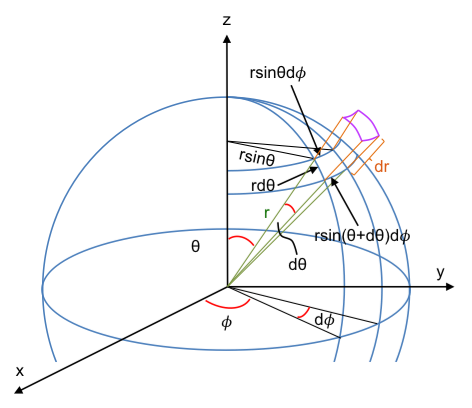
With reference to the above diagram, a control volume in spherical coordinates is given by:

$dV=r^2sin\theta drd\theta d\phi\;\;\;\;\;\;\;(1)$

where

r is the radius of the sphere

θ is the polar angle

Φ is the azimuthal angle

Substitute the formula for density V = m/ρ in eq1 and divide throughout by ∂t,

$\frac{\partial m}{\partial t}=\frac{\partial \rho}{\partial t}r^2sin\theta drd\theta d\phi\; \; \; \; \; \; \; (2)$

The flow velocity of the fluid is:

$\textbf{\textit{u}}=\textit u_r\hat{r}+\textit u_\theta\hat{\theta}+\textit u_\phi\hat{\phi}\; \; \; \; \; \; \; (3)$

The net flow of fluid through the surfaces of the control volume in the radial direction can be expressed as the rate of change of mass through the surfaces in the radial direction:

$\frac{\partial m_{out,r}}{\partial t}-\frac{\partial m_{in,r}}{\partial t}=(\rho u_r+\frac{\partial \rho u_r}{\partial r}dr)A_{out,r}-\rho u_rA_{in,r}\; \; \; \; \; \; \; (4)$

A_out,ris the outflow area of the control volume in the radial direction, given by:

$A_{out,r}=average\:length_{out}\:\times \:breadth_{out}$

$A_{out,r}=\frac{(r+dr)sin(\theta +d\theta)d\phi+(r+dr)sin\theta d\phi}{2}(r+dr)d\theta\; \; \; \; \; \; \; (5)$

Substituting sin(θ+dθ) ≈ sinθ + cosθdθ (from the Maclaurin series of cosθ and sinθ for small θ) in eq5 and eliminating higher order terms (i.e. terms with dr², dθ²):

$A_{out,r}=r^2sin\theta d\theta d\phi+2rsin\theta drd\theta d\phi\; \; \; \; \; \; \; (6)$

Similarly, the inflow area of the control volume in the radial direction A_in,ris:

$A_{in,r}=r^2sin\theta d\theta d\phi\; \; \; \; \; \; \; (7)$

Substituting eq6 and eq7 in eq4 and eliminating higher order terms,

$\frac{\partial m_{out,r}}{dt}-\frac{\partial m_{in,r}}{dt}=2\rho u_rrsin\theta drd\theta d\phi + r^2sin\theta \frac{\partial \rho u_r}{dr}drd\theta d\phi\; \; \; \; \; \; \; (8)$

Repeating the above steps for the net flow of fluid through the surfaces of the control volume in the polar and azimuthal directions, we have:

$\frac{\partial m_{out,\theta}}{dt}-\frac{\partial m_{in,\theta}}{dt}=\rho u_\theta rcos\theta drd\theta d\phi+ rsin\theta \frac{\partial \rho u_\theta}{\partial \theta}drd\theta d\phi \; \; \; \; \; \; \; (9)$

$\frac{\partial m_{out,\phi}}{dt}-\frac{\partial m_{in,\phi}}{dt}=r \frac{\partial \rho u_\phi}{\partial \phi}drd\theta d\phi \; \; \; \; \; \; \; (10)$

Assuming steady fluid flow and the conservation of fluid mass, the fluxes of mass into the control volume must be equal to the fluxes of mass out of the control volume and the accumulation of mass in the control volume:

$\frac{\partial m_{in,r}}{\partial t}+\frac{\partial m_{in,\theta}}{\partial t}+\frac{\partial m_{in,\phi}}{\partial t}=\frac{\partial m_{out,r}}{\partial t}+\frac{\partial m_{out,\theta}}{\partial t}+\frac{\partial m_{out,\phi}}{\partial t}+\frac{\partial m}{\partial t}\; \; \; \; \; \; \; (11)$

Substituting eq8, eq9 and eq10 in eq11, we have the continuity equation in spherical coordinates.

$\frac{\partial \rho}{\partial t}+\frac{1}{r^2}\frac{\partial \rho r^2u_r}{\partial r}+\frac{1}{rsin\theta} \frac{\partial \rho u_\theta sin\theta}{\partial \theta}+\frac{1}{rsin\theta} \frac{\partial \rho u_\phi}{\partial \phi}=0\; \; \; \; \; \; \; (12)$

where

$\frac{1}{rsin\theta} \frac{\partial \rho u_\theta sin\theta}{\partial \theta}=\frac{1}{r}\frac{\partial \rho u_\theta}{\partial \theta}+\rho u_\theta \frac{cos\theta}{rsin\theta}$

$\frac{1}{r^2} \frac{\partial \rho r^2u_r}{\partial r}=\frac{2}{r}\rho u_r+\frac{\partial \rho u_r}{\partial r}$

Continuity equation

NExt article: Stokes stream function

Previous article: Overview

Content page of Stokes’ law

Content page of advanced chemistry

Main content page