Robert Boyle, an Irish chemist, studied the relationship between the pressure and volume of a gas in 1662 by trapping a quantity of air in the close-end of a J-shaped tube of known cross sectional area with mercury (see diagram below).
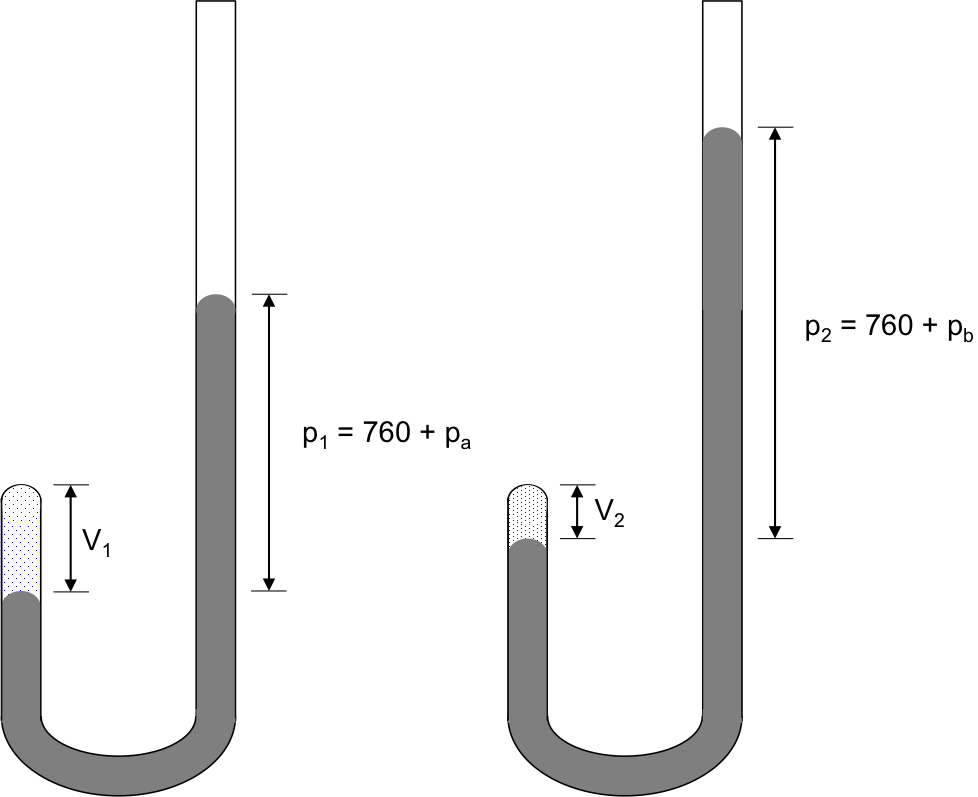
In the experiment, pressure exerted on the trapped gas equals the atmospheric pressure (760 mmHg) plus the pressure exerted by the column of mercury, pi, which is varied by pouring mercury into the longer arm of the tube via the open-end.
Boyle found that the product of the pressure and volume of a fixed amount of gas was constant at a given temperature.
where k1 is the proportionality constant. Eq1 is known as Boyle’s law, which states:
The volume of a given mass of gas is inversely proportional to its pressure at constant temperature
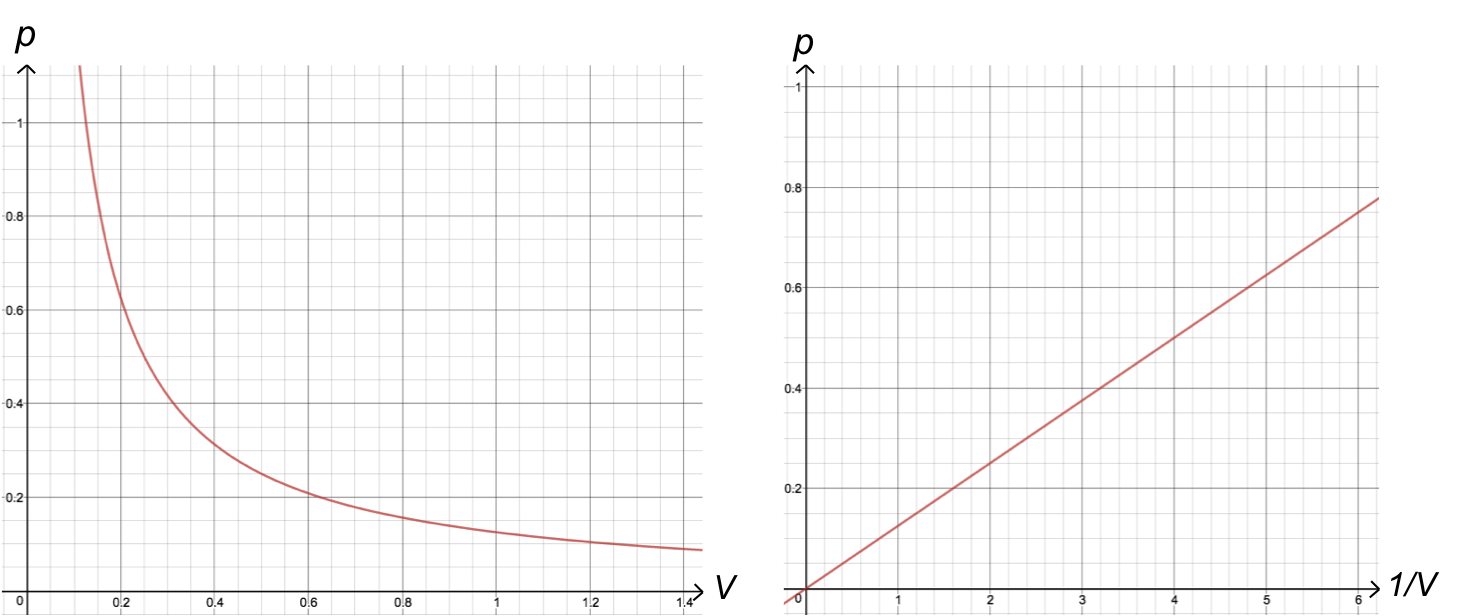
A plot of eq1 in terms of p versus V gives a hyperbola with the coordinate axes as asymptotes, while that of p versus 1/V produces a straight line with a gradient of k1 and an intercept at the origin.
Since p1V1 = k1 and p2V2 = k1, Boyle’s law can also be expressed as

Question
The volume of a bubble at the bottom of a lake with a depth of 30.0 m is 7.0 cm3. Assuming temperature remains constant, what is the bubble’s volume when it reaches the surface, where atmospheric pressure is equal to the pressure under 10.0 m of water?
Answer
Using eq2,