The one-particle, time-independent Schrodinger equation is a partial differential equation whose solutions are the one-particle, time-independent wave functions of quantum-mechanical systems.
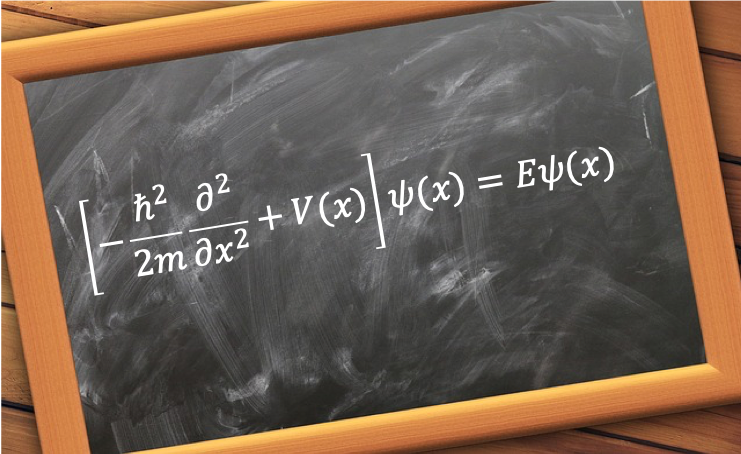
Even though it is widely regarded as a postulate, we can list the scientific findings that could have inspired Schrodinger to develop the equation.
| Year | Development | Formula | Scientist |
| 1500s | Equations of motion | Linear rotational motion equations | Many scientists including Galileo and Newton |
| 1746 | 1-D classical wave equation, whose solutions are wave functions that describe the motion of waves. | Jean d’Alembert | |
| 1924 | de Broglie’s hypothesis: all matter exhibit wave-like properties | Louis de Broglie |
Many scientists at that time were trying to develop models of the atom, in particular, the behaviour of electrons in an atom. It is possible that when de Broglie proposed that all matter have wave—like properties, Schrodinger thought that an equation similar to the classical wave equation could be derived to describe the wave motion of an electron in an atom. Since the classical wave equation is solved by the separation of variables method, we can express as
. Substituting
in the classical wave equation, we have:
Substitute and
in the above equation
The total energy of an electron is or
, where
is the momentum of the electron. Substituting
in de Broglie’s relation, we have
, which we then substitute in eq43 to give:
where , or
where .
is called the Hamiltonian operator and Eq44 is the one-dimensional, one-particle time-independent Schrodinger equation. As it is an eigenvalue equation,
(known as a wave function) is an eigenfunction and
is the corresponding eigenvalue. For a three-dimensional, one-particle system, the Hamiltonian is:
where and is called the Laplacian.
