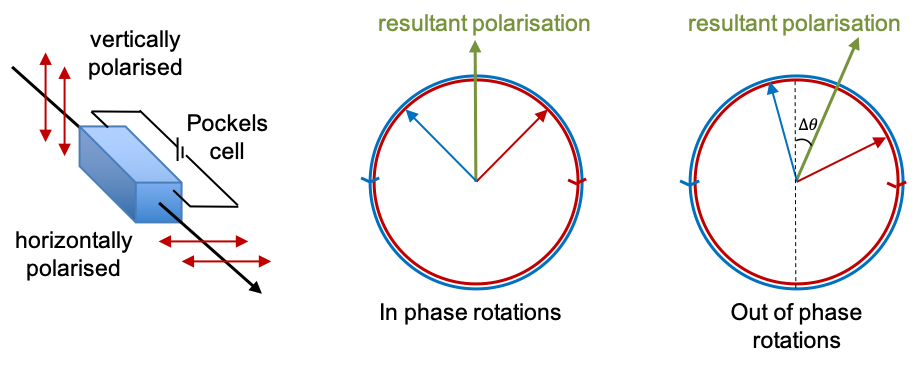
A Pockels cell is an electro-optical device that rotates the polarisation of light. It is based on the Pockels Effect, where the birefringence of the crystal in the cell changes linearly with an applied voltage (see diagram below).
An example of a crystal exhibiting the Pockels Effect is ammonium dihydrogen phosphate NH4H2PO4, which has a tetragonal crystal structure. It is aligned with its optic axis parallel to the propagation direction of the light. In the absence of an external electric field, the incoming beam suffers no birefringence. When an external electric field is applied across the crystal, the electron distribution of the crystal is distorted to the extent that the relative values of and
changes, with the degree of change being proportional to the applied voltage.
To explain the change in polarisation direction of light, let’s regard the vertically polarised light as a superposition of two circular light components that are rotating in phase with the same angular frequency but in opposite directions (see above diagram). When the external electric field is turned on, one component travels faster than the other in the Pockels cell. For a cell of length
, the difference in time
travelled by each component is:
where and
are the speeds of the two components in the cell.
Substitute the definition of refractive index (, where
is the speed of light in vacuum) and eq235 in eq236
Substitute the above equation in the definition of phase difference () between the two components,
As the birefringence of the crystal changes proportionally with voltage
, the phase difference
between the two circular components changes with an applied voltage. Since the angle of rotation of polarisation is
(you can visualise the rotation angle using the diagram above),
where is a proportionality constant, which is specific to the material used.
