Photon polarisation is the quantum mechanical treatment of light polarisation. Photoelectric effect experiments have shown that the direction of electron emission depends on the polarisation of the incident light. In quantum mechanics, classical polarisation directions are referred to as quantum states, with the states and
representing linear polarisation parallel to the
-axis and the
-axis respectively (see diagram below).
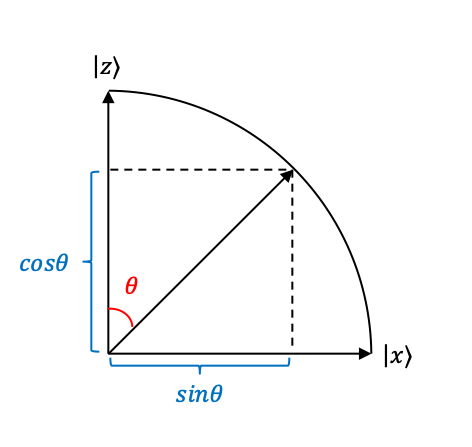
If we consider a unit circle, the state of a photon polarised at
with respect to the
-axis can therefore be written as a linear combination of
and
:
where and
become basis state vectors.
Since these basis vectors are unit vectors and
, we can express the state of the photon as
.

Question
Can a single photon be unpolarised?
Answer
Each photon in a string of photons (e.g. from the sun) has a definite polarisation, even though one photon’s oscillation direction may be randomly oriented relatively to another photon’s oscillation direction.
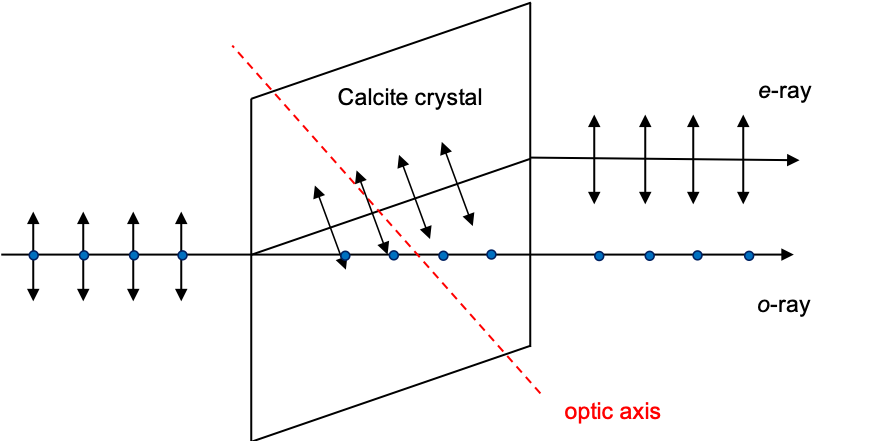
As per any normalised quantum state of , the square of each coefficient
is interpreted as the probability that a measurement of a system will yield an eigenvalue associated with the corresponding eigenstate
, i.e.
. If we measure the polarisation of a string of photons, whose generic states are given by eq237, using a calcite crystal (see diagram above; the optic axis lies in the plane of the viewer’s screen), photons with oscillations perpendicular to the plane of the screen emerge as part of the o-ray with the state
, while photons with oscillations parallel to the plane emerge as part of the e-ray with the state
. A photon oscillating at
(
) has 50% probability of emerging as part of the o-ray and 50% probability emerging as part of the e-ray.