Functional variation

Functional variation refers to the change in a functional’s output as a result of a small change in the functional’s input on a specified domain.

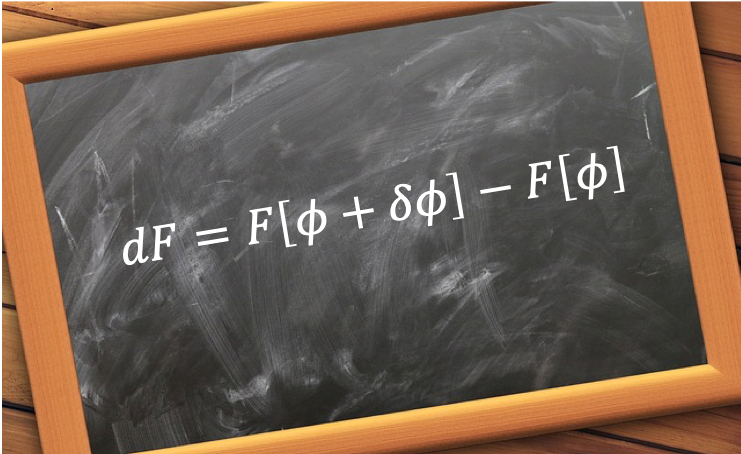
Question

What is a functional?

Answer

A functional is a function $F[\phi]$ whose value depends on a function $\phi$ instead of an independent variable. For example, the expectation value of the Hamiltonian is a functional, where $F[\phi]=\left\langle\phi\vert\hat{H}\vert\phi\right\rangle$ .

For a small variation in $\phi$ ,

$F[\phi+\delta\phi]=\left\langle\phi+\delta\phi\vert\hat{H}\vert\phi+\delta\phi\right\rangle=\left\langle\phi\vert\hat{H}\vert\phi\right\rangle+\left\langle\delta\phi\vert\hat{H}\vert\phi\right\rangle$ $+\left\langle\phi\vert\hat{H}\vert\delta\phi\right\rangle+\left\langle\delta\phi\vert\hat{H}\vert\delta\phi\right\rangle$

where $\delta\phi$ is a small arbitrary change in $\phi$ .

Since $\delta\phi$ is small, $\left<\delta\phi\vert\widehat{H}\vert\delta\phi\right>=c(\delta\phi)^2\approx 0$ , and

$F[\phi+\delta\phi]=\left<\phi\vert\widehat{H}\vert\phi\right>+\delta E=F[\phi]+\delta E$

where $\delta E=\left<\delta\phi\vert\widehat{H}\vert\phi\right>+\left<\phi\vert\widehat{H}\vert\delta\phi\right>$ .

If $\delta E=0$ , we have $F[\phi+\delta\phi]=F[\phi]$ or

$dF=F[\phi+\delta\phi]-F[\phi]=0\;\;\;\;\;\;\;\;(14a)$

which means that a small change in the functional’s input yields no change in the functional’s output. This implies a minimum energy according to the variational principle.

Functional variation

Question

Answer

Next article: Proof of HArtree equations

Previous article: Lagrange method of undetermined multipliers

Content page of computational chemistry

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply