In this article, we shall calculate the ground state energy of a helium atom in one-dimension using an Excel spreadsheet. From eq5, the equations to be solved iteratively are:
The presence of multiple functions and variables in each of these equations requires us to devise a computation strategy, the first of which is to derive a trial wavefunction.

Question
Show that is a reasonable wavefunction describing the helium ion.
Answer
The one-dimensional Schrodinger equation for the helium ion is , which can be written as
where ,
,
and
.
The general solutions of eq27 are of the form or
. Let’s use
, which is a modified form of a Slater-type orbital, where
for the helium ion. Since
, the normalisation constant N for y is
. So,
.
As the helium atom experiences an effective nuclear charge that is between that of a hydrogen atom () and a helium ion (
), it can expressed by the trial wavefunction
, which after normalisation is
Next, the pair of equations mentioned at the top of the article have two distinct wavefunctions, each representing one of the two electrons. To simplify our computation, we assume that the two electrons can be expressed by the same spatial wavefunction. This is known as the restricted case. To iteratively solve for the common wavefunction, we need to transform the two equations into a new pair of equations. Rearranging eq5 for helium in one-dimension, we have
where and
.
Substitute the definition of the 2nd derivative in eq29 and rearranging, we have
To prevent from being undefined when
, we modify the Coulomb integral by adding a small constant C to the denominator. It is found that
gives reasonable computation results. So,
The definition of the 1st derivative is
or:
Eq30 and eq31 are used in an iterative algorithm to find and
. The procedure is as follows:
1) Set the boundary condition and
. With reference to eq30, use eq28 as the initial guess wavefunction
for the Coulomb integral. Let’s also assume an initial guess gradient of
.
2) Let with intervals of
(350 intervals in total). This implies that
at
.
3) Use Simpson’s rule to integrate the Coulomb integral for all
. An example of the excel table is shown below.

With reference to eq24, the formulae for cells C4, D4 and E4 are =(C2^2)*EXP(-2*1.5*C2)/(ABS(B4-C2)+0.5), =4*(D2^2)*EXP(-2*1.5*D2)/(ABS(B4-D2)+0.5) and =2*(E2^2)*EXP(-2*1.5*E2)/(ABS(B4-E2)+0.5) respectively. The formula for cell MP4 is =SUM(B4:MN4). Finally, the formula for cell MQ is 13.5*7/350/3*MP4, where 13.5 is the square of the normalisation constant of eq28. The formulae for the remaining cells within C4:MQ354 are populated accordingly.
4) The iterative table is formulated as follows:

The second row is for guess values and the error function. Rows 4 to 354 are for the algorithm. Cells MS2 and MV2 are the initial guess values of and b respectively. The formula for the normalisation constant in cell MU2 is =SQRT(((-MV2*2)^3)/2). Cell MS4 is obviously zero. The formula for cell MT4 is =MS2. With reference to eq29 and eq28, the formulae for cells MS5 and MT5 are, =MS4+MT4*(B5-B4) and =MT4+(MQ5-(2/B5)-MT2)*2*MS5*(B5-B4) respectively. The formulae for the remaining cells within MS4:MT354 are populated accordingly.
Next, we plot a graph using values in cells MS4:MS354 as vertical coordinates and B4:B354 as horizontal coordinates. By visually inspecting the graph, the value in cell MT2 is manually adjusted so that when
. To optimise the values in cells MS2 and MV2, we include a trendline in the plot, where the formulae for cells MU4 and MU5 is zero and =MU2*B5*EXP(MV2*B5) respectively. The formulae for the remaining cells within MU4:MU354 are populated accordingly.
The error function formula in cell MW2 is {=SQRT(SUM((MS5:MS365-MU5:MU354)^2))}. The curly brackets {} are obtained by first typing the formula within {} in the cell and pressing CTRL+SHIFT+ENTER. Lastly, the Excel Solver application is use to optimise the values in cells MS2 and MV2, with the following settings:
Set objective: MW2
To: Min
By changing variable cells: MS2,MV2
Selecting a solving method: GRG Nonlinear
5) For the next set of iterations, repeat steps 3 and 4, where the guess values of MS2 and MV2 are the optimised values of the previous set of iterations. The value for MU is no longer the formula =SQRT(((-MV2*2)^3)/2) but the optimised normalisation constant of the previous set of iterations. Similarly, the values of and used in the Coulomb integral in step 3 are no longer and
but the optimised values of MU2 and MV2 of the previous set of iterations.
6) The cycle continues until the values of , N and b are invariant up to five decimal points.
The results are summarized below:
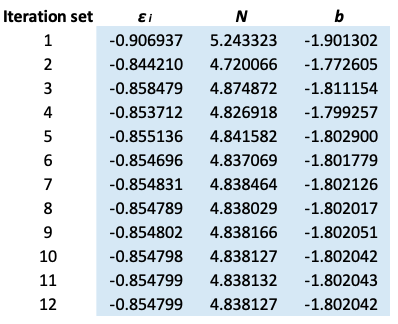
To find we use eq9, where
is taken from the 12th iteration set in the table above, while the double integral in eq32 is evaluated using form 2 of eq25. We being by computing the inner integral
as per step 3, using
and
. Next, we apply the Simpson rule a second time for the outer integral. The Excel table is as follows:

The formula for cell NA4 is =(4.838127^2)*(B4^2)*EXP(-1.802042*2*B4))*MQ4. With reference to form 2 of eq25, the formula in NC4 is =NA4*NB4*7/350/3, representing the double integral for . The formulae for the remaining cells within NA4:NB354 are populated accordingly. Summing NC4:NC354, we obtain the total value of the double integral of 1.1386946, which when substituted in eq32 together with
gives
. This theoretical value has a deviation of about 1.91% versus the experiment data of the ground state of helium.