Derivation of the root mean square speed of a gas

Consider a gas particle of mass $m$ moving in a container to the right with velocity $v$ (see diagram below). The change in momentum of the particle $\Delta p$ in the $x$ -coordinate before and after colliding elastically with a surface of the container is

$\Delta p=-mv_x-mv_x=-2mv_x\;\;\;\;\;\;\;\;(1)$

with the particle colliding the same surface every

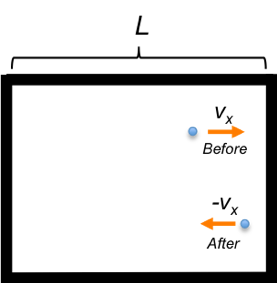
$\Delta t=\frac{dist}{speed}=\frac{2L}{\vert v_x\vert}\;\;\;\;\;\;\;\;(2)$

The force $F$ acting on the particle at collision is

$F=m\frac{\Delta v}{\Delta t}=\frac{\Delta p}{\Delta t}=-\frac{mv_x^2}{L}\;\;\;\;\;\;\;\;(3)$

By Newton’s third law, the force acting on the surface of the container by the particle is

$F=\frac{mv_x^2}{L}\;\;\;\;\;\;\;\;(4)$

The total force $F_T$ exerted on the surface by $N$ particles is

$F_T=\frac{mv_{x,1}^2}{L}+\frac{mv_{x,2}^2}{L}+\cdots+\frac{mv_{x,N}^2}{L}=\frac{Nm\overline{v_x^2}}{L}\;\;\;\;\;\;\;\;(5)$

where $\overline{v_x^2}=\frac{v_{x,1}^2+v_{x,2}^2+\cdots+v_{x,N}^2}{N}$ .

Comparing $\overline{v_x^2}$ and the definition of root mean square speed, we have $\overline{v_x^2}=v_{x,rms}^2$ , i.e. the square of the root mean square speed of the gas in the $x$ -direction.

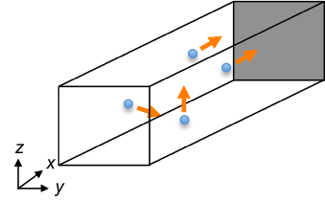
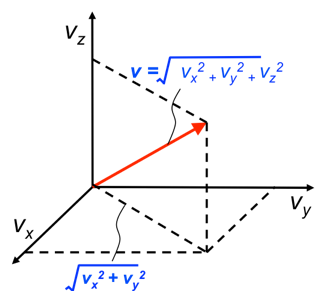
If the container is three dimensional (see above diagram), the velocity vector for a particle in Cartesian coordinates in three dimensions is:

$v^2=v_x^2+v_y^2+v_z^2\;\;\;\;\;\;\;\;(6)$

Even though a particle has three velocity components in space, the force exerted on the shaded wall is dependent only on the $x$ -component velocity of the particle.

To express the root mean square speed for $N$ particles, let’s begin by summing the squares of the velocity vectors of all particles:

$v_1^2+v_2^2+\cdots+v_N^2=(v_{x,1}^2+v_{y,1}^2+\cdots+v_{z,1}^2)+(v_{x,2}^2+v_{y,2}^2+\cdots+v_{z,2}^2)+\cdots+(v_{x,N}^2+v_{y,N}^2+\cdots+v_{z,N}^2)$

Next, group the velocity components and divide the equation throughout by $N$ ,

$\frac{v_1^2+v_2^2+\cdots+v_N^2}{N}=\frac{(v_{x,1}^2+v_{x,2}^2+\cdots+v_{x,N}^2)}{N}+\frac{(v_{y,1}^2+v_{y,2}^2+\cdots+v_{y,N}^2)}{N}+\cdots+\frac{(v_{z,1}^2+v_{z,2}^2+\cdots+v_{z,N}^2)}{N}$

$\overline{v^2}=\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2}\;\;\;\;\;\;\;\;(7)$

The velocity components of the particles in the container are assumed to be random, with the particles being evenly distributed in the container at any time. $v_x$ , like $v_y$ and $v_z$ , can be positive or negative but their squares, $v_x^2$ , $v_y^2$ and $v_z^2$ are always positive. If the velocity components of the particles in the container are random, and the number of particles is very large,

$\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}\;\;\;\;\;\;\;\;(8)$

Otherwise, there is a preference of direction in a particular axis and the particles’ movement is no longer random (you can convince yourself the validity of eq8 by summing the squares of three sets of randomly generated numbers in a spreadsheet and finding their averages; the larger the number of elements in each set, the closer the average values are to each other). Hence, we can rewrite eq7 as:

$\overline{v^2}=3\overline{v_x^2}\;\;\;\;\;\;\;\;(9)$

Substitute eq9 in eq5

$F_T=\frac{Nm\overline{v^2}}{3L}\;\;\;\;\;\;\;\;(10)$

The pressure $p$ (not to be confused with momentum) exerted by $N$ particles on the shaded wall is

$p=\frac{F_T}{A}=\frac{Nm\overline{v^2}}{3V}$

where $V$ is the volume of the container.

Hence,

$pV=\frac{1}{3}Nm\overline{v^2}=\frac{2}{3}N\left(\frac{1}{2}m\overline{v^2}\right)\;\;\;\;\;\;\;\;(11)$

Substitute the ideal gas law in eq11,

$nRT=\frac{1}{3}Nm\overline{v^2}=\frac{2}{3}N\left(\frac{1}{2}m\overline{v^2}\right)\;\;\;\;\;\;\;\;(11)$

Since $R=N_Ak$ and $N=nN_A$ ,

$nkT=\frac{2}{3}n\left(\frac{1}{2}m\overline{v^2}\right)$

$\frac{3}{2}kT=\frac{1}{2}m\overline{v^2}=\langle KE\rangle\;\;\;\;\;\;\;\;(12)$

Since $\overline{v^2}=\frac{v_1^2+v_2^2+\cdots+v_N^2}{N}$ and the root mean square speed is $v_{rms}=\sqrt{\frac{v_1^2+v_2^2+\cdots+v_N^2}{N}}$ , we have $\overline{v^2}=v_{rms}^2$ . Therefore,