The decomposition of a reducible representation of a group reduces it to the direct sum of irreducible representations of the group. We have shown in an earlier article that this involves decomposing a block diagonal matrix into the direct sum of its constituent square matrices. In this article, we shall derive some useful equations involving the characters of the representations of a group (see eq25, eq27a, eq29 and eq30 below).
Consider an element of a reducible representation that has undergone a similarity transformation to the following block diagonal matrix:
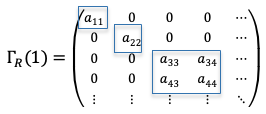
where ,
,
and
.
Clearly, . Since the trace of a matrix belonging to the
-th class of the
-th irreducible representation is called the character of a class
, we have
. However, a particular constituent irreducible representation may appear more than once in the decomposition. Therefore,
where is the number of times
appear in the direct sum.
Multiplying eq25 by , where
is the number of elements in the
-th class, and sum over
,
Substituting eq23 in eq26,
Since ,
Eq27 is sometimes written as a sum over the individual symmetry operations rather than over the various classes:

Question
Show that .
Answer
The complex conjugate of eq25, with a change of the dummy index from to
, is
. Multiply this by eq25 and by
and sum over
,
Swap the dummy indices of eq23 to , which when substituted in the above equation, gives
Since ,
With reference to eq25 and eq28, if one of the is equal to 1, with the rest of the
equal to zero, then
is an irreducible representation. This implies that

Question
Show that if two reducible representations and
of a group
are equivalent, they decompose into the same direct sum of irreducible representations of
.
Answer
Since and
are related by a similarity transformation,
for every
. Using eq27a,