The recurrence relations of the Legendre polynomials describe how each polynomial in the sequence can be obtained from its predecessors.
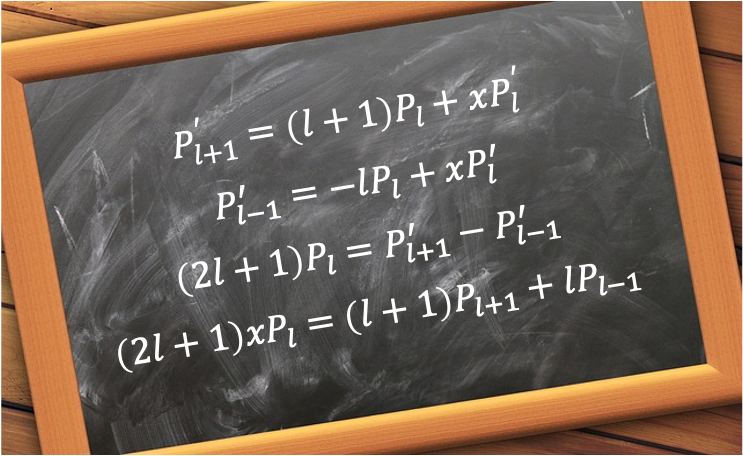
Some useful recurrence relations of the Legendre polynomials include
where .
To derive these relations, we differentiate eq345 with respect to and
to give
and
respectively.
Substituting eq345 in eq346f yields
Equating the coefficents of gives
Substituting eq346e in eq346f results in . When we equate the coefficients of
in this equation, we get eq346b. Combining eq346b and eq346g gives eq346a. Substracting eq346b from eq346a yields eq346c.
The last recurrence relation is obtained by substituting eq345 in eq346e to give . Expanding and equating coefficients of
, we have eq346d.