The internal energy 
of a thermodynamic system consisting of non-interacting particles can be represented statistically using the molecular partition function 
.
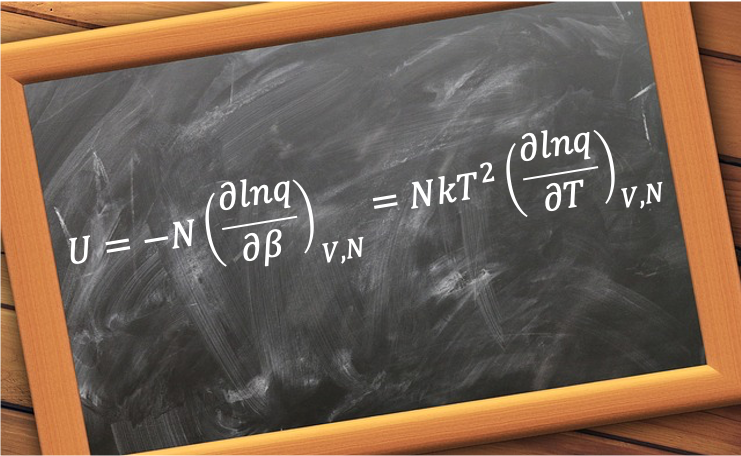
It is equivalent to the product of the mean molecular energy 
and the number of non-interacting particles 
in the system. From eq320, where 
, we have:
_{V,N}\;\;\;\;\;\;\;\;360)
As mentioned in an earlier article, 
is the total molecular partition function (i.e. eq257), with contributions from translational, rotational, vibrational and electronic degrees of freedom. Eq360 assumes that all components of , including 
, are defined using absolute energy levels — for example, the vibrational molecular partition function includes the zero-point energy (i.e. eq290). However, if is instead defined relative to the zero-point energy (i.e. eq292), then we need to add back the zero-point energy term 
giving:
}{\partial T}\biggr\]_{V,N}\\&=U_T+U_R+U_V+U_E\;\;\;\;\;\;\;\;361\end{align})
where _{V,N})
.
Monatomic ideal gas
For a monatomic ideal gas, each atom is a point mass with no rotational or vibrational degrees of freedom. This implies that there is only a single rotational ground state and a single vibrational ground state, each with energy equal to zero. Therefore, 
. Furthermore, as explained in the derivation of eq297, 
for an atom not subjected to extreme temperatures. Hence, eq361 simplifies to:
_{V,N}\;\;\;\;\;\;\;\;362)
Substituting eq266 into eq362 and differentiating gives:
Comparing eq363 with eq305, 
. Substituting 
, where 
is the Avogadro constant and 
is the number of moles, into eq363 yields:
where the universal gas constant is 
.
Diatomic ideal gas
For a diatomic ideal gas, 
is again given by eq363. 
is derived by substituting eq275 into _{V,N})
and differentiating to give:
Comparing eq364 with eq309, 
.
For 
, we substitute eq293 into _{V,N})
and differentiating to give:
where 
.
At high but not extreme temperatures, 
, which allows us to expand 
as a Taylor series (
) to give:
Comparing eq366 with eq313, 
.
Similar to an atom, for a diatomic molecule (see derivation of eq297). Hence,
_{V,N}=0\;\;\;\;\;\;\;\;367)
which is consistent with eq316.
The total internal energy of a system of a diatomic ideal gas not subjected to extreme temperatures is therefore:
Polyatomic ideal gas
The translational component of the internal energy of a polyatomic ideal gas is again:
As mentioned in this article, each normal mode of vibration of a polyatmomic molecule behaves approximately like a separate harmonic oscillator, with the total vibrational partition function given by eq294:
where 
for non-linear molecules, 
for linear molecules, and 
is the number of atoms per molecule.
Substituting 
into of of and differentiating gives:
It follows that at high but not extreme temperatures,
for a linear rotor is derived by substituting eq275 into and differentiating to yield:
for a non-linear rotor (including spherical, symmetric and asymmetric rotors), is derived by substituting either eq280, eq286 or eq287 into and differentiating to give:
Once again, for a polyatomic molecule not subjected to extreme temperatures. Therefore, the total internal energy of a system of a polyatomic ideal gas not subjected to extreme temperatures is:
nRT\;\;\;\;\;linear\;molecules)
nRT\;\;\;\;\;non-linear\;molecules)