The exclusion rule in vibrational spectroscopy states that, for molecules with a centre of symmetry, a vibrational mode that is infrared-active is Raman-inactive, and a mode that is Raman-active is infrared-inactive.
From a group‐theoretical perspective, the exclusion rule follows from the symmetry properties of the operators that govern infrared and Raman transitions. A vibrational mode is IR-active if its irreducible representation transforms like one of the linear basis functions (Cartesian coordinates) ,
, or
, because the electric dipole moment operator has the same symmetry. It is Raman-active if its irreducible representation appears in the symmetry of the quadratic basis functions
,
,
,
,
, or
, which correspond to components of the polarisability tensor.
A point group to which a centrosymmetric molecule belongs always includes the inversion symmetry operator. Each of the basis functions ,
, or
changes sign (e.g.
) when it is inverted through the origin. On the other hand, quadratic basis functions, which are products of two linear functions, do not change sign upon inversion because both linear functions constituting the quadratic function change sign (e.g.
and
).
This implies that the character corresponding to the inversion operation of an irreducible representation associated with a linear basis function is always different from that associated with a quadratic basis function. It follows that irreducible representations that are ungerade (u) can be IR-active but cannot be Raman-active, while irreducible representations that are gerade (g) can be Raman-active but cannot be IR-active. In other words, no vibrational mode of centrosymmetric molecules can be both IR- and Raman-active, which is the essence of the mutual exclusion rule.

This principle is clearly illustrated by the vibrational spectrum of CO2, which has four vibrational modes belonging to the point group. The symmetric stretching vibration transforms as the
irreducible representation and is therefore Raman-active but IR-inactive. In contrast, the asymmetric stretching vibration transforms as
, which only has the same symmetry as the
function, making it IR-active but Raman-inactive. The two bending vibrational modes are doubly degenerate and transform as the
irreducible representation, which corresponds to the
and
functions. Consequently, the bending modes are also IR-active and Raman-inactive. Thus, no mode is simultaneously IR- and Raman-active.
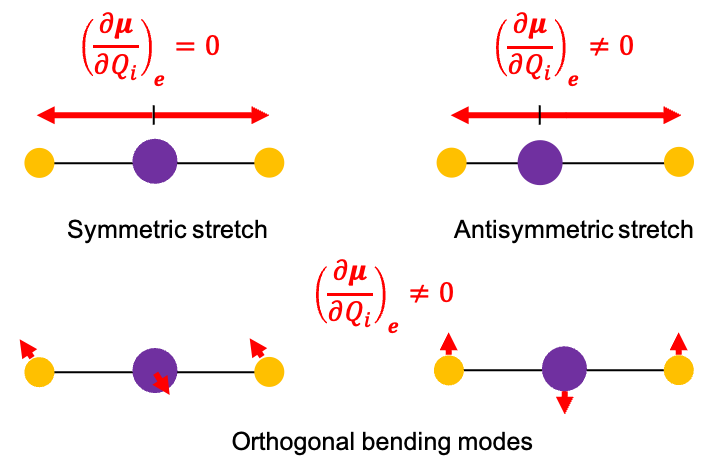
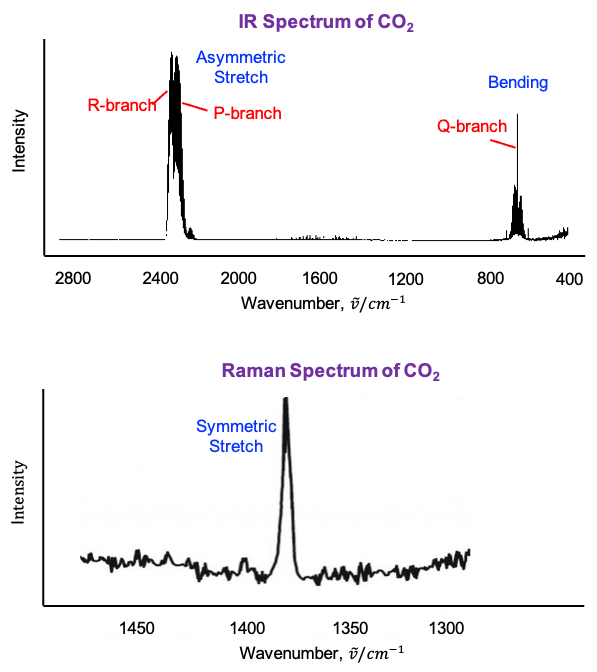
Accordingly, the IR spectrum of CO2 contains absorption bands corresponding to the asymmetric stretch and the bending vibrations, whereas the Raman spectrum shows a strong band associated with the symmetric stretch (see diagram below).

Question
Is the vibrational mode of O2 IR-active or Raman-active?
Answer
O2 vibrates by simply moving its two atoms closer and farther apart. Since both atoms are identical, this stretching mode is perfectly symmetric and transforms according to the irreducible representation of the
point group. Therefore, it is Raman-active but not IR-active.