The crystallographic restriction theorem generally states that the rotational symmetries of a crystal are limited.
We have seen from a previous section that a lattice is formed by repeating lattice points that have the same environment. It is this fundamental geometric property of a lattice that restricts the number of rotational symmetries of a space lattice and hence the types of unit cells.
To illustrate the crystallographic restriction theorem, let’s consider a row of lattice points (indicated by the line connecting blue dots in figure I of the below diagram) that are equally spaced by the basis vector a.
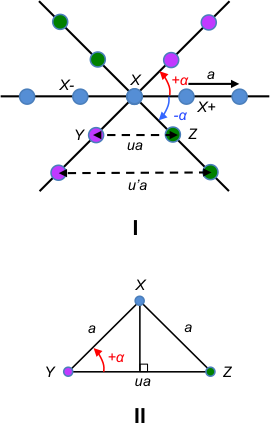
Assuming that the lattice has a rotational symmetry given by the angle , a rotation about the lattice point X by +
, around an axis perpendicular to the plane of this page, maps the blue lattice point X- to the pink lattice point Y. Similarly, a rotation about the same lattice point X by –
maps the blue lattice point X+ to the green lattice point Z.
Since the rotations are symmetry operations, Y and Z are also lattice points. As mentioned in an earlier article, the lattice points in a two-dimensional lattice are described by the position vector r = ua + vb where u, v ∈ . Therefore, YZ must be a lattice vector separated by an integer multiple of a, i.e. YZ = ua + 0b or YZ = ua, where u ∈
. With reference to figure II of the above diagram,
Since -1 ≤ cos ≤ 1,
Substituting eq5 in eq4, the possible values of are 180o, 120o, 90o, 60o, 0o (or 360o). As we have assumed that a rotation of the lattice by the angle
transforms the lattice into a state that is indistinguishable from the starting state, the possible values of
correspond to 2-, 3-, 4-, 6- and 1-fold symmetry of the two-dimensional lattice.
For a space lattice in three dimensions, consider a three-dimensional lattice vector r = ua + vb + wc that is neither parallel nor perpendicular to the axis of rotation (see diagram below). A rotation by maps r onto another lattice vector r’ that has the same magnitude as r. Since both r and r’ are lattice vectors, their difference r’ – r is also a lattice vector, which lies on a plane that is perpendicular to the axis of rotation.
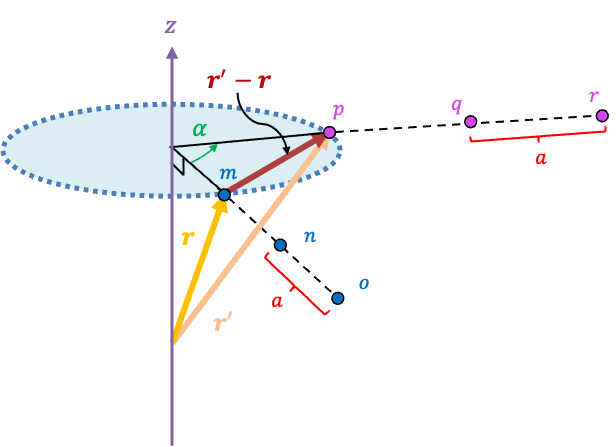
By varying the integers u, v and w, we can extend m to a row of points mno that are spaced apart. This reduces a three-dimensional lattice proof of the crystallographic restriction theorem to a two-dimensional one, which is already given above.
We have proven the crystallographic restriction theorem with trigonometry. The proof can also be made with linear algebra (see this article).

