Determinant of a matrix

The determinant is a number associated with an $n\times n$ matrix $A$ . It is defined as

$\vert A\vert=\begin{cases}\vert a_{11}\vert=a_{11}&n=1\\\sum_{j=1}^na_{1j}A_{1j}&n > 1\end{cases}$

where

1. $a_{1j}$ is an element of in the first row of $A$ .
2. $A_{1j}=(-1)^{1+j}M_{1j}^A$ is the cofactor associated with $A$ .
3. $M_{1j}^A$ , the minor of the element $A_{1j}$ , is the determinant of the $n-1 \times n-1$ matrix obtained by removing the $i=1$ row and $j$ -th column of $A$ .

In the case of $n > 1$ , we say that the summation is a cofactor expansion along row 1. For example, the determinant of $A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$ is

$\vert A\vert=a_{11}\biggr\vert\begin{matrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{matrix}\biggr\vert-a_{12}\biggr\vert\begin{matrix}a_{21}&a_{23}\\a_{31}&a_{33}\end{matrix}\biggr\vert+a_{13}\biggr\vert\begin{matrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{matrix}\biggr\vert$

For any square matrix, the cofactor expansion along any row and any column results in the same determinant, i.e.

$\vert A\vert=\begin{cases}\vert a_{11}\vert=a_{11}&n=1\\\sum_{i\;or\;j=1}^na_{ij}A_{ij}&n > 1\end{cases}$

To prove this, we begin with the proof that the cofactor expansion along any row results in the same determinant, i.e. $\vert A\vert=\sum_{j=1}^na_{ij}(-1)^{i+j}M_{ij}^A$ for $n > 1$ . Consider a matrix $B$ , which is obtained from $A$ by swapping row $i$ consecutively with rows above it $i-1$ times until it resides in row 1. According to property 8 (see below), we have

$\vert A\vert=(-1)^{i-1}\vert B\vert=(-1)^{i-1}\sum_{j=1}^nb_{1j}(-1)^{1+j}M_{1j}^B\\=(-1)^{i-1}\sum_{j=1}^na_{ij}(-1)^{1+j}M_{ij}^A=\sum_{j=1}^na_{ij}(-1)^{i+j}M_{ij}^A$

According to property 10, $\vert A\vert=\vert A^T\vert$ and therefore, the cofactor expansion along any column also results in the same determinant. This concludes the proof.

In short, to calculate the determinant of an $n > 1$ matrix, we can carry out the cofactor expansion along any row or column. If we expand along a row, we have $\vert A\vert=\sum_{j=1}^na_{ij}A_{ij}$ . We then select any row $i$ to execute the summation. Conversely, if we expand along a column, we get $\vert A\vert=\sum_{i=1}^na_{ij}A_{ij}$ .

The following are some useful properties of determinants:

1. $\vert I\vert=1$ , where is $I$ the identity matrix. If one of the diagonal elements of $I$ is $k$ , then $\vert I'\vert=k$ .
2. $\vert cI\vert=c^n$
3. If the elements of one of the columns of $A$ are all zero, $\vert A\vert=0$ .
4. If $B$ is obtained from $A$ by multiplying the $p$ -th row of $A$ by $k$ , $\vert B\vert=k\vert A\vert$ .
5. $\vert \varepsilon A\vert=\vert\varepsilon\vert\vert A\vert$
6. $\vert AB\vert=\vert A\vert\vert B\vert$
7. $\vert cA\vert=c^n\vert A\vert$
8. If $B$ is obtained from $A$ by swapping two rows or columns of $A$ , then $\vert B\vert=-\vert A\vert$
9. If two rows or two columns of $A$ are the same, $\vert A\vert=0$ .
10. $\vert A\vert=\vert A^T\vert$
11. The inverse of a matrix exists only if $\vert A\vert\neq 0$ .
12. If $\vert A\vert= 0$ , then $\vert AB\vert=0$ .
13. If $\vert A\vert\neq 0$ , then $\vert A^T\vert\neq 0$ . If $\vert A\vert= 0$ , then $\vert A^T\vert= 0$ .
14. If $A$ is diagonal, then $\vert A\vert= \prod_{i=1}^na_{ii}$ .

Proof of property 1

We shall proof this property by induction.

For $n=1$ ,

$\vert I\vert=\vert 1\vert=1$

For $n=2$ ,

$\sum_{j=1}^2i_{1j}I_{1j}=(1)(-1)^2M_{11}+(0)(-1)^3M_{12}=(1)(-1)^2(1)=1$

Let’s assume that for $n=n-1$ , $\vert I\vert=\sum_{j=1}^{n-1}i_{1j}I_{1j}=1$ . Then for $n=n$ ,

$\vert I\vert=\sum_{j=1}^ni_{1j}I_{1j}=i_{1n}I_{1n}+\sum_{j=1}^{n-1}i_{1j}I_{1j}=(0)I_{1n}+1=1$

We can repeat the above induction logic to prove that $\vert I'\vert=k$ if one of the diagonal elements of $I$ is $k$ .

Proof of property 2

Again, we shall proof this property by induction.

For $n=1$ ,

$\vert cI\vert_1=\vert c\vert=c$

For $n=2$ ,

$\vert cI\vert_2=\sum_{j=1}^2i_{1j}I_{1j}=c(1)(-1)^2M_{11}+c(0)(-1)^3M_{12}=c\vert ci_{22}\vert=c(c)=c^2$

Let’s assume that for $n=n-1$ , we have $\vert cI\vert_{n-1}=c^{n-1}$ . Then for $n=n$ ,

$\vert cI\vert_n=\sum_{j=1}^nci_{1j}I_{1j}=ci_{11}I_{11}+ci_{12}I_{12}+\cdots +ci_{1n}I_{1n}\\=c(1)I_{11}+c(0)I_{12}+\cdots+c(0)I_{1n}=cI_{11}=c\vert cI\vert_{n-1}=cc^{n-1}=c^n$

Proof of property 3

For $n-1$ , where $a_{11}=0$ , we have $\vert A\vert=0$ . For $n>1$ , the definition $\vert A\vert=\sum_{i\;or\;j=1}^na_{ij}A_{ij}$ allows us to sum by row or by column. Suppose we sum by row, we have $\vert A\vert=\sum_{i=1}^na_{ij}A_{ij}$ . Since we are allowed to choose any column $j$ to execute the summation, we can always select the column $j=k$ such that $a_{ik}=0$ . Therefore, $\vert A\vert=0$ if the elements of one of the columns of are all zero.

Proof of property 4

Let’s suppose $B$ is obtained from $A$ by multiplying the $p$ -th row of $A$ by $k$ . If we expand $\vert A\vert$ and $\vert B\vert$ along row $p$ , cofactor $B_{pj}$ is equal to cofactor $A_{pj}$ . Therefore,

$\vert B\vert=\sum_{j=1}^nb_{pj}B_{pj}=\sum_{j=1}^nka_{pj}A_{pj}=k\vert A\vert$

Proof of property 5

For a type I elementary matrix, $\varepsilon A$ transforms $A$ by swapping two rows of $A$ . So, $\vert\varepsilon A\vert=-\vert A\vert$ due to property 8. Since $\varepsilon$ is obtained from $I$ by swapping two rows of $I$ , we have $\vert\varepsilon\vert=-1$ according to property 1 and property 8, which implies that $\vert\varepsilon\vert\vert A\vert=-\vert A\vert$ . Therefore, $\vert\varepsilon A\vert=\vert\varepsilon\vert\vert A\vert$ .

For a type II elementary matrix, $\vert\varepsilon A\vert=k\vert A\vert$ due to property 4 and $\vert\varepsilon\vert\vert A\vert=k\vert A\vert$ because of property 1. So, $\vert\varepsilon A\vert=\vert\varepsilon\vert\vert A\vert$ .

For a type III elementary matrix,

$\vert \varepsilon A\vert=\sum_{j=1}^n(a_{pj}+ka_{qj})A_{pj}=\sum_{j=1}^na_{pj}A_{pj}+k\sum_{j=1}^na_{qj}A_{pj}=\vert A\vert+k\vert B\vert$

$\vert A\vert=\sum_{j=1}^na_{pj}A_{pj}$ is computed by expanding along row $p$ . The equation $\vert B\vert=\sum_{j=1}^na_{qj}A_{pj}$ means that when $\vert B\vert$ is computed by expanding along row $p$ , it has the same cofactor as when $\vert A\vert$ is computed by expanding along row $p$ . This implies that $b_{qj}=a_{qj}$ . Since the definition of the determinant of $B$ is $\vert B\vert=\sum_{j=1}^nb_{pj}B_{pj}$ , which in our case is equivalent to $\vert B\vert=\sum_{j=1}^na_{qj}A_{pj}$ , we have $b_{pj}=a_{qj}$ . Thus $b_{pj}=b_{qj}$ , which according to property 9, gives:

$\vert \varepsilon A\vert=\vert A\vert\;\;\;\;\;\;\;\;5$

Since $\varepsilon =\varepsilon I$ ,

$\vert \varepsilon \vert=\vert \varepsilon I\vert=\vert I\vert=1\;\;\;\;\;\;\;\;6$

according to eq5 and property 1.

Comparing eq5 and eq6, $\vert\varepsilon A\vert=\vert\varepsilon\vert\vert A\vert$ .

Proof of property 6

Case 1

If $A$ is singular, where $\vert A\vert=0$ , then $AB$ is also singular according to property 12. So, $\vert AB\vert=\vert A\vert\vert B\vert$ .

Case 2

If $A$ is non-singular, it can always be expressed as a product of elementary matrices: $A=\varepsilon_1\varepsilon_2\cdots\varepsilon_k$ . So,

$\vert AB\vert=\vert\varepsilon_1(\varepsilon_2\cdots\varepsilon_kB)\vert$

Since property 5 states that $\vert \varepsilon M\vert=\vert\varepsilon\vert\vert M\vert$ ,

$\vert AB\vert=\vert\varepsilon_1\vert\vert\varepsilon_2\cdots\varepsilon_kB\vert=\vert\varepsilon_1\vert\vert\varepsilon_2\vert\vert\varepsilon_3\cdots\varepsilon_kB\vert=\cdots=\vert\varepsilon_1\vert\vert\varepsilon_2\vert\cdots\vert\varepsilon_k\vert\vert B\vert$

Similarly, $\vert A\vert=\vert\varepsilon_1(\varepsilon_2\cdots\varepsilon_k)\vert=\vert\varepsilon_1\vert\vert\varepsilon_2\vert\cdots\vert\varepsilon_k\vert$ . Substitute this in the above equation, $\vert AB\vert=\vert A\vert\vert B\vert$ .

Proof of property 7

Using property 6 and then property 2,

$\vert cA\vert=\vert cIA\vert=\vert cI\vert\vert A\vert=c^n\vert A\vert$

Proof of property 8

We shall proof this property by induction. $n=1$ is the trivial case, where $n$ is the rank of a square matrix.

For $n=2$ , let $A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$ and $A=\begin{pmatrix}a_{21}&a_{22}\\a_{11}&a_{12}\end{pmatrix}$ , which is obtained from $A$ by swapping two adjacent rows. Furthermore, let $\vert A\vert=\sum_{j=1}^na_{1j}(-1)^{1+j}m_{1j}^A$ and $\vert B\vert=\sum_{j=1}^nb_{1j}(-1)^{1+j}m_{1j}^B$ . Clearly,

$\vert B\vert=a_{21}a_{12}-a_{22}a_{11}=-(a_{11}a_{22}-a_{12}a_{21})=-\vert A\vert$

Let’s assume that for $n=k$ , $\vert B\vert=-\vert A\vert$ when two adjacent rows are swapped. For $n=k+1$ , we have:

Case 1: Suppose that the first row of $A$ is not swapped when making $B$ .

$\vert B\vert=\sum_{j=1}^nb_{1j}(-1)^{1+j}M_{1j}^B=\sum_{j=1}^na_{1j}(-1)^{1+j}M_{1j}^B$

$M_{1j}^B$ is the determinant of a rank $k$ matrix, which is the same as $M_{1j}^A$ except for two adjacent rows being swapped. Therefore, $M_{1j}^B=-M_{1j}^A$ and $\vert B\vert=-\sum_{j=1}^na_{1j}(-1)^{1+j}M_{1j}^A=-\vert A\vert$ .

Case 2: If the first two rows of $A$ are swapped when making $B$ ,

$A=\begin{pmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{pmatrix}\;\;\; B=\begin{pmatrix}b_{11}&b_{12}&\cdots&b_{1n}\\b_{21}&b_{22}&\cdots&b_{2n}\\\vdots&\vdots&\ddots&\vdots\\b_{n1}&b_{n2}&\cdots&b_{nn}\end{pmatrix}=\begin{pmatrix}a_{21}&a_{22}&\cdots&a_{2n}\\a_{11}&a_{12}&\cdots&a_{1n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{pmatrix}$

We have $\vert A\vert=\sum_{j=1}^na_{1j}(-1)^{1+j}M_{1j}^A$ and $\vert B\vert=\sum_{k=1}^nb_{1k}(-1)^{1+k}M_{1k}^B=\sum_{k=1}^na_{2k}(-1)^{1+k}M_{1k}^B$ . The minors $M_{1j}^A$ and $M_{1k}^B$ can be expressed as

$M_{1j}^A=(1-\delta_{1j})\sum_{k=1}^{j-1}a_{2k}(-1)^{1+k}\vert A_{kj}\vert+\sum_{k=j+1}^na_{2k}(-1)^{k}\vert A_{jk}\vert$

$M_{1k}^B=(1-\delta_{1k})\sum_{j=1}^{k-1}a_{1j}(-1)^{1+j}\vert A_{jk}\vert+\sum_{j=k+1}^na_{1j}(-1)^{j}\vert A_{kj}\vert$

where $A_{kj\;or\;jk}$ is $A$ with the first two rows, and the $k$ -th and $j$ -th columns removed.

Question

Why is each of the minors expressed as two separate sums?

Answer

The minor $M_{1j}^A$ is the determinant of a submatrix of $A$ with the first row and the $j$ -th column of $A$ removed. If $j=1$ , the term with the Kronecker delta disappears and $M_{11}^A=\sum_{k=2}^na_{2k}(-1)^k\vert A_{1k}\vert$ , where $\vert A_{1k}\vert$ is the determinant of $A$ with the first two rows, and the $k$ -th and 1st columns removed. If $1<j<n$ , one of the columns between the 1^st and the last columns of $A$ is removed in forming the submatrix. Therefore, both summations are employed in determining $M_{1j}^A$ , with the first from $k=1$ to $k=j-1$ and the second from $k=j+1$ to $k=n$ . The two summations also apply to the case when $j=n$ . Finally, the same logic can be used to explain the formula for $M_{1k}^B$ . You can validate the formulae of both minors using the example of:

Therefore,

$\vert A\vert=\sum_{j=1}^na_{1j}(-1)^{1+j}\biggr\[(1-\delta_{1j})\sum_{k=1}^{j-1}a_{2k}(-1)^{1+k}\vert A_{kj}\vert+\sum_{k=j+1}^na_{2k}(-1)^{k}\vert A_{jk}\vert\biggr\]$

$\vert B\vert=\sum_{k=1}^na_{2k}(-1)^{1+k}\biggr\[(1-\delta_{1k})\sum_{j=1}^{k-1}a_{1j}(-1)^{1+j}\vert A_{jk}\vert+\sum_{j=k+1}^na_{1j}(-1)^{j}\vert A_{kj}\vert\biggr\]$

For any pair of values of $j$ and $k$ , where $k<j$ , the terms in $\vert A\vert$ are $a_{1j}(-1)^{1+j}\sum_{k=1}^{j-1}a_{2k}(-1)^{1+k}\vert A_{kj}\vert$ , which differ from the terms in $\vert B\vert$ , i.e. $a_{2k}(-1)^{1+k}\sum_{j=k+1}^{n}a_{1j}(-1)^{j}\vert A_{kj}\vert$ , by a factor of -1. Similarly, for any pair of values of $j$ and $k$ , where $k>j$ , the terms in $\vert A\vert$ are $a_{1j}(-1)^{1+j}\sum_{k=j+1}^{n}a_{2k}(-1)^{k}\vert A_{jk}\vert$ , which again differ from the terms in $\vert B\vert$ , i.e. $a_{2k}(-1)^{1+k}\sum_{j=1}^{k-1}a_{1j}(-1)^{1+j}\vert A_{jk}\vert$ , by a factor of -1. Since all terms in $\vert A\vert$ differ from all corresponding terms in $\vert B\vert$ by a factor of -1, $\vert B\vert=-\vert A\vert$ .

In general, the swapping of any two rows $p$ and $q$ of $A$ , where $1\leq p<q\leq n$ , is equivalent to the swapping of $2(q-p)-1$ adjacent rows of $A$ , with each swap changing $\vert A\vert$ by a factor of -1. Therefore,

$\vert B\vert=(-1)^{2(q-p)-1}\vert A\vert=[(-1)^2]^{p-q}(-1)^{-1}\vert A\vert=-\vert A\vert$

Question

How do we get $2(q-p)-1$ ?

Answer

Firstly, we swap row $p$ consecutively with each row below it until row $q$ is swapped, resulting in $q-p$ swaps. Then, swap the previous row $q$ , which now resides in what was row $q-1$ , consecutively with each row above it until it becomes what used to be row $p$ , resulting in $q-1-p$ swaps. These two actions combined are equivalent to the swapping of $p$ with $q$ , with a total of $2(q-p)-1$ swaps of adjacent rows. The diagram below illustrates an example of the swaps:

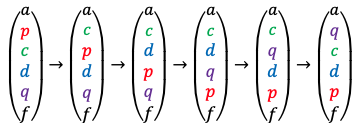
Finally, the swapping of any two columns is proven in a similar way.

Proof of property 9

Consider the swapping of two equal rows of $A$ to form $B$ , resulting in $B=A$ and $\vert B\vert=\vert A\vert$ . However, property 8 states that $\vert B\vert=-\vert A\vert$ if any two rows of are swapped. Therefore, $\vert B\vert=\vert A\vert=0$ if two rows of $A$ are equal. The same logic applies to proving $\vert A\vert=0$ if there are two equal columns of $A$ .

Proof of property 10

Case 1: $\vert A\vert=0$

If $\vert A\vert=0$ , then $\vert A^T\vert=0$ according to property 13. So, $\vert A\vert=0=\vert A^T\vert$ .

Case 2: $\vert A\vert\neq 0$

Let’s first consider elementary matrices $\varepsilon$ . A type I elementary matrix is symmetrical about its diagonal, while a type II elementary matrix has one diagonal element equal to $k$ . Therefore, $\varepsilon=\varepsilon^T$ and thus $\vert \varepsilon\vert=\vert\varepsilon^T\vert$ for type I or II elementary matrices. A type III elementary matrix is an identity matrix with one of the non-diagonal elements replaced by a constant $k$ . Therefore, if $\varepsilon$ is a type III elementary matrix, then $\varepsilon^T$ is also one. According to eq6, $\vert\varepsilon\vert=1=\vert\varepsilon^T\vert$ for a type III elementary matrix. Hence, $\vert\varepsilon\vert=\vert\varepsilon^T\vert$ for all elementary matrices.

Next, consider an invertible matrix $A$ , which (as proven in the previous article) can be expressed as $A=\varepsilon_1\varepsilon_2\cdots\varepsilon_k$ . Thus, $A^T=(\varepsilon_1\varepsilon_2\cdots\varepsilon_k)^T=\varepsilon_k^T\cdots\varepsilon_2^T\varepsilon_1^T$ (see Q&A in the proof of property 13). According to property 5,

$\vert A^T\vert=\vert\varepsilon_k^T\cdots\varepsilon_2^T\varepsilon_1^T\vert=\vert\varepsilon_k^T\vert\vert\varepsilon_{k-1}^T\cdots\varepsilon_1^T\vert=\cdots=\vert\varepsilon_k^T\vert\cdots\vert\varepsilon_2^T\vert\vert\varepsilon_1^T\vert=\vert\varepsilon_k\vert\cdots\vert\varepsilon_2\vert\vert\varepsilon_1\vert$

and

$\vert A\vert=\vert\varepsilon_1\varepsilon_2\cdots\varepsilon_k\vert=\vert\varepsilon_1\vert\vert\varepsilon_2\cdots\varepsilon_k\vert=\cdots=\vert\varepsilon_1\vert\vert\varepsilon_2\vert\cdots\vert\varepsilon_k\vert$

Therefore, $\vert A\vert=\vert A^T\vert$ .

Proof of property 11

We have $A^{-1}A=I$ , or in terms of matrix components:

$\sum_{k=1}^n(a^{-1})_{qk}a_{kp}=\delta_{pq}=\frac{\vert A\vert}{\vert A\vert}\delta_{pq}\;\;\;\;\;\;\;\;7$

Consider the matrix $B$ that is obtained from the matrix $A$ by replacing the $q$ -th column of $A$ with the $p$ -th column, i.e. $b_{kq}=a_{kp}$ for $1\leq k\leq n$ and $p\neq q$ . According to property 9, $\vert B\vert=0$ because $B$ has two equal columns. Furthermore, cofactor $B_{kq}$ is equal to cofactor $A_{kq}$ for $1\leq k\leq n$ . Therefore,

$0=\vert B\vert=\sum_{k=1}^nb_{kq}B_{kq}=\sum_{k=1}^na_{kp}A_{kq}\;\;\;\;p\neq q\;\;\;\;\;\;\;\;8$

When $q=p$ , the last summation in eq8 becomes

$\sum_{k=1}^na_{kp}A_{kp}=\vert A\vert\;\;\;\;\;\;\;\;9$

Combining eq8 and eq9, we have $\sum_{k=1}^na_{kp}A_{kq}=\vert A\vert\delta_{pq}$ , which when substituted in eq7 gives:

$\sum_{k=1}^n(a^{-1})_{qk}a_{kp}=\sum_{k=1}^n\frac{A_{kq}}{\vert A\vert}a_{kp}$

Therefore, $(a^{-1})_{qk}=\frac{A_{kq}}{\vert A\vert}$ , which implies that the inverse of a matrix is undefined if $\vert A\vert=0$ . In other words, the inverse of a matrix $A$ is undefined if $\vert A\vert=0$ . We call such a matrix, a singular matrix, and a matrix with an associated inverse, a non-singular matrix.

Proof of property 12

We shall prove by contradiction. According to property 11, $A$ has no inverse if $\vert A\vert=0$ . If $A$ has no inverse and $AB$ has an inverse, then $A\[B(AB)^{-1}\]=I$ . This implies that $A$ has an inverse $A^{-1}$ , where $A^{-1}=B(AB)^{-1}$ , which contradicts the initial assumption that $A$ has no inverse. Therefore, if $A$ has no inverse, then $AB$ must also have no inverse.

Proof of property 13

Question

Show that $(ABC\cdots)^T=\cdots C^TB^TA^T$ .

Answer

$(AB)^T=B^TA^T$ because

$(AB)^T_{ij}=(AB)_{ji}=\sum_{k=1}^na_{jk}b_{ki}=\sum_{k=1}^n(A^T)_{kj}(B^T)_{ik}\\=\sum_{k=1}^n(B^T)_{ik}(A^T)_{kj}=(B^TA^T)_{ij}$

$(ABC)^T=C^TB^TA^T$ because

$(ABC)^T_{ij}=(ABC)_{ji}=\sum_{l=1}^n\sum_{k=1}^na_{jk}b_{kl}c_{li}=\sum_{l=1}^n\sum_{k=1}^n(A^T)_{kj}(B^T)_{lk}(C^T)_{il}\\=\sum_{l=1}^n\sum_{k=1}^n(C^T)_{il}(B^T)_{lk}(A^T)_{kj}=(C^TB^TA^T)_{ij}$

which can be extended to $(ABC\cdots)^T=\cdots C^TB^TA^T$ .

Using the identity in the above Q&A, $(A^{-1})^TA^T=(AA^{-1})^T$ . If $A$ is invertible, then $(A^{-1})^TA^T=(AA^{-1})^T=I=(A^{-1}A)^T=A^T(A^{-1})^T$ . This implies that $(A^{-1})^T$ is the inverse of $A^T$ and therefore that $A^T$ is invertible if $A$ is invertible.

The last part shall be proven by contradiction. Suppose $A$ is singular and $A^T$ is non-singular, there would be a matrix $B$ such that $BA^T=I$ , Furthermore, $I=I^T=(BA^T)^T=AB^T$ , which implies that $B^T=A^{-1}$ . This contradicts our initial assumption that $A$ is singular. Therefore, if $A$ is singular, $A^T$ must also be singular.

Proof of property 14

We shall proof this property by induction. For $n=2$ ,

$\vert A\vert=a_{11}a_{22}=\prod_{i=1}^2a_{ii}$

Let’s assume that $\vert A\vert=\prod_{i=1}^na_{ii}$ for $n=n$ . Then for $n=n+1$ , the cofactor expansion along the first row is

$\vert A\vert=a_{11}\begin{vmatrix}a_{22}&0&\cdots&0\\0&a_{33}&\cdots&0\\0&0&\ddots&\vdots\\0&0&\cdots&a_{n+1,n+1}\end{vmatrix}=a_{11}\prod_{i=2}^{n+1}a_{ii}=\prod_{i=1}^{n+1}a_{ii}$

Determinant of a matrix

Question

Answer

Question

Answer

Question

Answer

Next article: Schur’s first lemma

Previous article: Elementary row operation and elementary matrix

Content page of group theory

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply