Decomposition of group representations

The decomposition of a reducible representation of a group reduces it to the direct sum of irreducible representations of the group. We have shown in an earlier article that this involves decomposing a block diagonal matrix into the direct sum of its constituent square matrices. In this article, we shall derive some useful equations involving the characters of the representations of a group (see eq25, eq27a, eq29 and eq30 below).

Consider an element of a reducible representation $\Gamma_R(1)$ that has undergone a similarity transformation to the following block diagonal matrix:

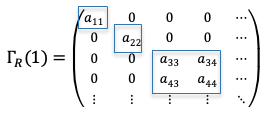
where $a_{11}=tr\[\Gamma_1(1)\]$ , $a_{22}=tr\[\Gamma_2(1)\]$ , $a_{33}+a_{44}=tr\[\Gamma_3(1)\]$ and $\Gamma_{R}(1)=\Gamma_1(1)\oplus\Gamma_2(1)\oplus\Gamma_3(1)\oplus\cdots$ .

Clearly, $tr\[\Gamma_R(1)\]=\sum_ktr\[\Gamma_k(1)\]$ . Since the trace of a matrix belonging to the $\alpha$ -th class of the $k$ -th irreducible representation is called the character of a class $\chi_k(\alpha)$ , we have $\chi_R(1)=\sum_ktr\[\Gamma_k(1)\]=\sum_k\chi_k(1)$ . However, a particular constituent irreducible representation may appear more than once in the decomposition. Therefore,

$\chi_R(\alpha)=\sum_kc_k\chi_k(\alpha)\;\;\;\;\;\;\;\;25$

where $c_k$ is the number of times $\chi_k(\alpha)$ appear in the direct sum.

Multiplying eq25 by $n_{\alpha}\chi_{k'}^*(\alpha)$ , where $n_{\alpha}$ is the number of elements in the $\alpha$ -th class, and sum over $\alpha$ ,

$\sum_{\alpha}n_{\alpha}\chi_{k'}^*(\alpha)\chi_R(\alpha)=\sum_kc_k\sum_{\alpha}n_{\alpha}\chi_{k'}^*(\alpha)\chi_k(\alpha)\;\;\;\;\;\;\;\;26$

Substituting eq23 in eq26,

$\sum_{\alpha}n_{\alpha}\chi_{k'}^*(\alpha)\chi_R(\alpha)=\vert G\vert\sum_kc_k\delta_{kk'}$

Since $\sum_kc_k\delta_{kk'}=c_1\delta_{1k'}+c_2\delta_{2k'}+\cdots+c_{k'}\delta_{k'k'}+\cdots=c_{k'}$ ,

$c_{k'}=\frac{1}{\vert G\vert}\sum_{\alpha}n_{\alpha}\chi_{k'}^*(\alpha)\chi_R(\alpha)\;\;\;\;\;\;\;\;27$

Eq27 is sometimes written as a sum over the individual symmetry operations $\beta$ rather than over the various classes:

$c_{k'}=\frac{1}{\vert G\vert}\sum_{\beta}\chi_{k'}^*(\beta)\chi_R(\beta)\;\;\;\;\;\;\;\;27a$

Question

Show that $\sum_{\alpha}n_{\alpha}\vert\chi_R(\alpha)\vert^2=\vert G\vert\sum_kc_k^2$ .

Answer

The complex conjugate of eq25, with a change of the dummy index from $k$ to $k'$ , is $\chi_R^*(\alpha)=\sum_{k'}c_{k'}\chi_{k'}^*(\alpha)$ . Multiply this by eq25 and by $n_{\alpha}$ and sum over $\alpha$ ,

$\sum_{\alpha}n_{\alpha}\chi_R^*(\alpha)\chi_R(\alpha)=\sum_k\sum_{k'}c_{k'}c_k\sum_{\alpha}n_{\alpha}\chi_{k'}^*(\alpha)\chi_k(\alpha)$

Swap the dummy indices of eq23 to $\sum_{\alpha=1}^Cn_{\alpha}\chi_{k'}^*(\alpha)\chi_k(\alpha)=\vert G\vert\delta_{k'k}$ , which when substituted in the above equation, gives

$\sum_{\alpha}n_{\alpha}\vert\chi_R(\alpha)\vert^2=\vert G\vert\sum_k\sum_{k'}c_{k'}c_k\delta_{k'k}$

Since $\sum_k\sum_{k'}c_{k'}c_k\delta_{k'k}=\sum_k(c_1c_k\delta_{1k}+c_2c_k\delta_{2k}+\cdots+c_kc_k\delta_{kk}+\cdots )=\sum_kc_k^2$ ,

$\sum_{\alpha}n_{\alpha}\vert\chi_R(\alpha)\vert^2=\vert G\vert\sum_kc_k^2\;\;\;\;\;\;\;\;28$

With reference to eq25 and eq28, if one of the $c_k$ is equal to 1, with the rest of the $c_k$ equal to zero, then $\chi_R(\alpha)$ is an irreducible representation. This implies that

$\sum_{\alpha}n_{\alpha}\vert\chi_k(\alpha)\vert^2=\vert G\vert\;\;\;for\;an\;irreducible\;representation\;\;\;\;\;\;\;\;29$

$\sum_{\alpha}n_{\alpha}\vert\chi_k(\alpha)\vert^2>\vert G\vert\;\;\;for\;a\;reducible\;representation\;\;\;\;\;\;\;\;30$

Question

Show that if two reducible representations $\Gamma_R$ and $\Gamma_R^{'}$ of a group $G$ are equivalent, they decompose into the same direct sum of irreducible representations of $G$ .

Answer

Since $\Gamma_R(\beta)$ and $\Gamma_R^{'}(\beta)$ are related by a similarity transformation, $tr\[\Gamma_R(\beta)\]=tr\[\Gamma_R^{'}(\beta)\]$ for every $\beta\in G$ . Using eq27a,

$c_{k'}=\frac{1}{\vert G\vert}\sum_{\beta}\chi_{k'}^*(\beta)tr\[\Gamma_R(\beta)\]=\frac{1}{\vert G\vert}\sum_{\beta}\chi_{k'}^*(\beta)tr\[\Gamma_R^{'}(\beta)\]$

Decomposition of group representations

Question

Answer

Question

Answer

Next article: Regular representation

Previous article: Little orthogonality theorem

Content page of group theory

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply