The rigid rotor

The rigid rotor is a fundamental model in quantum mechanics used to describe the rotational motion of a molecule, particularly diatomic molecules, where the two atoms are treated as point masses connected by a fixed-length bond. This simplification assumes that the molecule does not vibrate or stretch during rotation, allowing the system to be treated as a rigid body rotating in space. The model works reasonably well in the microwave frequency range of 10¹¹ to 10¹² Hz and provides critical insights into energy levels associated with molecular rotation.

For the more general case of a diatomic molecule’s internal motion (encompassing both rotational and vibrational motions), the Schrödinger equation for the two particles, can be derived by reducing the two-particle problem to a one-particle problem. The result is given by eq311:

$\left[\frac{\hat{p}_\mu^2}{2\mu}+V(R)\right]\psi_{\mu}(R,\theta,\phi)=E_{\mu}\psi_{\mu}(R,\theta,\phi)$

where

$\frac{p_\mu^2}{2\mu}$ is the kinetic energy operator of the internal motion of the system,
$\mu$ is the reduced mass of the molecule,
$V(R)$ is the internuclear potential energy ,
$\psi_{\mu}(R,\theta,\phi)$ is the molecular wavefunction in spherical coordinates,
$E\mu$ is the eigenvalue corresponding to the wavefunction.

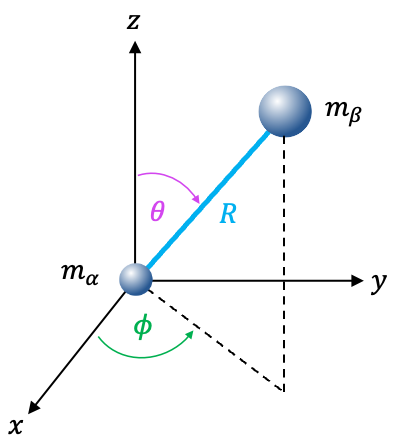
Within the rigid rotor approximation, the bond length is fixed ( $R=r$ is a constant) and $V(R)=0$ . The above equation simplifies to a rotational Schrödinger equation:

$\frac{\hat{p}_\mu^2}{2\mu}\psi_{\mu}(\theta,\phi)=E_{\mu}\psi_{\mu}(\theta,\phi)\;\;\;\;\;\;\;\;1$

Eq1 is equivalent to a Schrödinger equation for a particle of mass $\mu$ constrained to a spherical surface of zero relative potential and radius $r$ . The eigenfunctions of this system are the spherical harmonics $Y_l^{m_l}(\theta,\phi)$ , and the Hamiltonian can be explicitly written as (see eq50 of an eariler article):

$\frac{\hat{p}_\mu^2}{2\mu}=\hat{H}_{rot}=\frac{\hat{L}^2}{2I}=\frac{\hat{L}^2}{2\mu r^2}\;\;\;\;\;\;\;\;2$

Here, $I$ is the moment of inertia and $\hat{L}^2$ is the square of the angular momentum operator, with eigenvalues (see eq133):

$\hat{L}^2\vert l,m_l\rangle=l(l+1)\hbar^2\vert l,m_l\rangle$

Replacing $l$ with $J$ , the rotational quantum number, the energy of the rigid rotor is:

$E=\frac{J(J+1)\hbar^2}{2\mu r^2}\;\;\;\;\;J=0,1,2,\cdots\;\;\;\;\;\;\;\;3$

Eq3 can also be derived from classical mechanics, where the rotational kinetic energy of a particle with reduced mass $\mu$ is

$KE_{rot}=\frac{1}{2}\mu v_{\perp}^2=\frac{1}{2}\mu r^2\omega^2=\frac{1}{2}I\omega^2\;\;\;\;\;\;\;\;4$

with $I=\mu r^2$ and $v_{\perp}=\frac{2\pi r}{T}=r\omega$ , where $\omega$ is the magnitude of the angular velocity vector $\boldsymbol{\mathit{\omega}}=(\omega_x,\omega_y,\omega_z)$ .

Substituting the classical angular momentum $L=I\omega$ into eq4 yields

$KE_{rot}=\frac{L^2}{2I}$

Using the quantum mechanics postulate that “to every observable quantity in classical mechanics there corresponds a linear, Hermitian operator in quantum mechanics”, and replacing the classical angular momentum $L$ with the quantum mechanical operator gives

$\hat{H}_{rot}=\frac{\hat{L}^2}{2I}\;\;\;\;or\;\;\;\;\hat{H}_{rot}=\frac{\hat{J}^2}{2I}\;\;\;\;\;\;\;\;4a$
which is equivalent to eq2, and hence allows us to derive eq3.

The same postulate also enables us to derive similar energy expressions for polyatomic molecules. However, we must first examine the different moments of inertia for some common classes of polyatomic molecules, and to do that, we need to understand the parallel axis theorem.

Question

How many axes of rotation does a diatomic molecule have? If it has more than one, why is there only one moment of inertia mathematical expression $I=\mu r^2$ ?

Answer

A diatomic molecule has three principal axes of rotation that pass through its centre of mass and are mutually perpendicular, just like any rigid body. However, since the molecule is linear, the axis aligned with the bond (commonly taken as the z-axis) passes through both atoms, meaning the mass has no perpendicular displacement from this axis. As a result, the moment of inertia about this axis is zero: $I_z=0$ .

The other two axes, both perpendicular to the bond, are physically equivalent due to the molecule’s cylindrical symmetry. Rotation about either of these axes produces the same resistance to rotation, leading to equal moments of inertia: $I_x=I_y=\mu r^2$ . Therefore, although the molecule has three rotational axes, only one unique, nonzero moment of inertia expression is needed.

In other words, different axes of rotation will have different moments of inertia. In general, for a rigid body rotating in 3D space, the moment of inertia can be conveniently expressed as the following matrix, called the inertia tensor:

$\boldsymbol{\mathit{I}}=\begin{pmatrix}I_x&0&0\\0&I_y&0\\0&0&I_z\end{pmatrix}$

with

$\boldsymbol{\mathit{L=I\omega}}=\begin{pmatrix}I_x&0&0\\0&I_y&0\\0&0&I_z\end{pmatrix}\begin{pmatrix}\omega_x\\\omega_y\\\omega_z\end{pmatrix}=\begin{pmatrix}L_x\\L_y\\L_z\end{pmatrix}\;\;\;\;\;\;\;\;4b$

where $L_x=I_x\omega_x$ , $L_y=I_y\omega_y$ and $L_z=I_z\omega_z$ .

Eq4b states that $\boldsymbol{\mathit{L}}=\boldsymbol{\mathit{i}}L_x+\boldsymbol{\mathit{y}}L_y+\boldsymbol{\mathit{k}}L_z$ , which is consistent with classical mechanics (see this article). It follows that:

$\begin{align}KE_{rot}&=\frac{1}{2}\boldsymbol{\mathit{\omega^TI\omega}}\\&=\frac{1}{2}\begin{pmatrix}\omega_x&\omega_y&\omega_z\end{pmatrix}\begin{pmatrix}I_x&0&0\\0&I_y&0\\0&0&I_z\end{pmatrix}\begin{pmatrix}\omega_x\\\omega_y\\\omega_z\end{pmatrix}\\&=\frac{1}{2}I_x\omega_x^2+\frac{1}{2}I_y\omega_y^2+\frac{1}{2}I_z\omega_z^2\;\;\;\;\;\;\;\;4c\end{align}$

Question

Why is $KE_{rot}=\frac{1}{2}\boldsymbol{\mathit{\omega^TI\omega}}$ , and not $KE_{rot}=\frac{1}{2}\boldsymbol{\mathit{I\omega^T\omega}}$ or $KE_{rot}=\frac{1}{2}\boldsymbol{\mathit{I\omega\omega^T}}$ ?

Answer

$KE_{rot}$ is a scalar, and only $\frac{1}{2}\boldsymbol{\mathit{\omega^TI\omega}}$ evaluates to a scalar. The other two expressions result in matrices and are not valid for representing energy.

Substituting $L_x=I_x\omega_x$ , $L_y=I_y\omega_y$ and $L_z=I_z\omega_z$ back into eq4c gives

$KE_{rot}=\frac{L_x^2}{2I_x}+\frac{L_y^2}{2I_y}+\frac{L_z^2}{2I_z}$

and hence

$KE_{rot}=\frac{\hat{J}_x^2}{2I_x}+\frac{\hat{J}_y^2}{2I_y}+\frac{\hat{J}_z^2}{2I_z}\;\;\;\;\;\;\;\;4d$

Question

Answer

Question

Answer

Next article: Parallel axis theorem

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply