The moments of inertia of a trigonal planar oblate rotor with symmetry (e.g. BF3) are characterised by a unique moment of inertia
around the principal axis and two equal moments of inertia
perpendicular to the principal axis, where
. They are derived using simple geometric considerations.
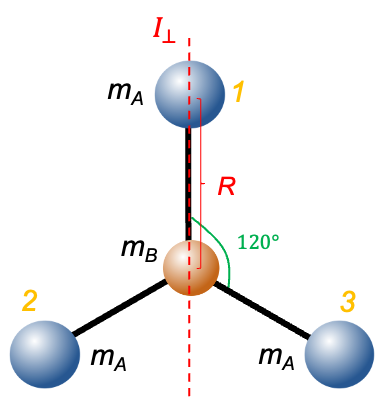
The diagram above shows a trigonal planar oblate rotor with its centre of mass located at atom B (of mass ), which is positioned at the origin
. The three A atoms (1,2 and 3), each with mass
, are equally spaced at 120° apart on an imaginary circle of radius
.
The moment of inertia along the -axis, which is perpendicular to the plane of the diagram, is
. Since the three B-A bonds have equal lengths of
, we have

Question
Why do not contribute to
?
Answer
In general, . Since atom B lie along the rotational axis, the moment of inertia about this axis is effectively zero due to the absence of perpendicular mass displacement (
).
To derive , we can make use of the coordinates of the atoms that form the base of a trigonal pyramidal molecule mentioned in an earlier article, where
and
:
| Atom | Coordinates | |
| Trigonal pyramidal | Trigonal planar | |
| A1 | ||
| A2 | ||
| A3 | ||
Therefore, or
Similarly, .