Microwave spectra represent the electromagnetic radiation absorbed or emitted by molecules when they undergo transitions between discrete rotational energy levels. These spectra are a key component in the study of molecular structure and dynamics. They provide valuable insights about molecular properties, such as bond lengths and moments of inertia.
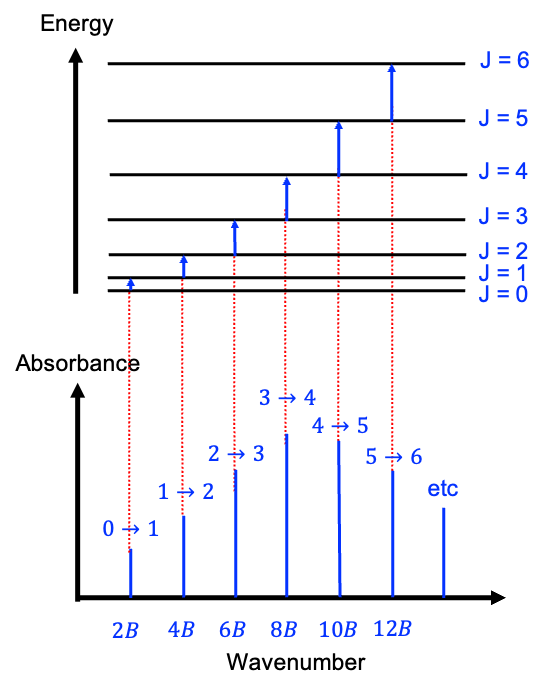
An ideal pure rotational spectrum of a rigid linear molecule, generated in the microwave frequency range of 1011 to 1012 Hz, typically exhibits a series of absorption lines that correspond to the rotational transitions of the molecule between discrete rotational energy levels (see diagram below). In the absence of an external magnetic field, these transitions follow the selection rule 
, meaning that a molecule can only transition between adjacent rotational levels.
The rotational energy levels are given by eq44 or eq45 and the frequencies of the transitions are directly related to the rotational constant 
, and as such, the spacing between the spectral lines provides information about the moment of inertia and the molecular structure. Using the definition )
, we have
(J+2)-J(J+1)]=2B(J+1)\;\;\;\;\;\;\;\;80)
Therefore, the first peak, obtained by substituting 
into eq80, lies at the point 
along the horizontal axis. Similarly, the second and third peaks are at 
and 
respectively. In other words, the peaks in an ideal rotational spectrum (without centrifugal distortion) of a rigid linear rotor are equally spaced at .
The intensity of each transition 
depends on the population of the initial level 
, which is governed by the Boltzmann distribution, with higher- states being less populated at lower temperatures:
where
is the Boltzmann constant.
is the number of particles in the energy state 
.
is the total number of particles in the system.
Since 
represents the fraction of particles in the state , the intensity of a spectral line is proportional to 
, where the value corresponds to a specific energy level. However, there are )
degenerate states associated with each value of in a rigid linear molecule. This degeneracy increases the statistical weight of higher levels, redistributing the population towards more degenerate states, which become thermally accessible at typical laboratory temperatures. In other words, at a given temperature, more particles will occupy a higher state with greater degeneracy at equilibrium than they would if the state were non-degenerate. Therefore, when a sample is exposed to an external microwave field, the intensity 
of each allowed transition in the pure rotational spectrum is proportional to the population of the initial state, which is the product of and . This gives:
e^{-\frac{hcBJ(J+1)}{kT}}\;\;\;\;\;\;\;\;81)
where 
is a proportionality constant and is given by eq45.
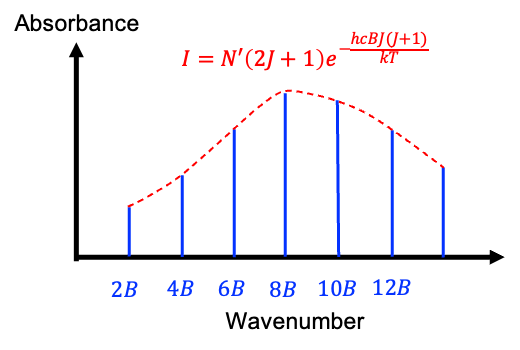
The factor in eq81 increases linearly with , while the exponential term decreases exponentially. As a result, the graph of versus forms a skewed bell curve (see diagram above), with a maximum found by treating as a continuous variable and taking the derivative of with respect to :
}{kT}}\biggr\[2-(2J+1)^2\frac{hcB}{kT}\biggr\])
Setting 
, and noting that }{kT}}\neq 0)
for any finite , gives
Since must be an integer, the maximum intensity occurs at the value of closest to the result of eq82.
Question
Is the intensity of each transition dependent on the electric dipole moment?
Answer
Although the transition probability between adjacent rotational states is proportional to _{l',m'_l}\vert\boldsymbol{\mathit{\hat{\mu}}}\vert\psi(\theta,\phi)_{l,m_l}\rangle\vert^2)
, which depends on the magnitude of the electric dipole moment, the sample molecules in the waveguide of a typical microwave spectrometer are randomly oriented. As a result, the effect transition dipole moment does not vary significantly from one transition to the next for a given molecule. Therefore, while the absolute intensity depends on the dipole moment, it is often treated as a constant factor when comparing transitions within the same molecule.
For a symmetric rotor, +K^2(\tilde{A}-\tilde{B}))
and 
is also given by eq80. However, the spectrum is not just a single series of equally spaced lines like that of a linear rotor. Instead, each value of 
is associated with a series of lines with equal spacing of 
. In other words, a symmetric top spectrum consists of multiple superimposed series of equally spaced lines, each corresponding to a different value of 
. As a result, the individual lines may not be as clearly resolved and may appear as a denser pattern compared to that of a linear molecule. Nevertheless, the overall intensity envelope of the spectrum still resembles a skewed bell curve, with the maximum intensity occurring at the value where the population is highest.
In practice, the peaks in a real rotational spectrum are not vertical lines but have finite width and shape, appearing as broadened curves. This broadening arises, under typical laboratory conditions, from several effects:
-
- Doppler broadening, due to the thermal motion of molecules, causes a spread in observed frequencies as molecules move towards or away from the detector.
- Instrumental broadening results from the finite resolution of the spectrometer itself.
Beyond broadening, other phenomena affect the detailed structure and spacing of the spectral lines:
-
- Centrifugal distortion causes deviations from the ideal rigid rotor model. As rotational speed increases with higher levels, the molecular bond stretches slightly, increasing the moment of inertia and decreasing the rotational constant . This leads to uneven spacing between lines, especially at higher , and is accounted for using a correction term.
-
- Isotopic substitution alters the moment of inertia due to the change in atomic mass, thereby changing the rotational constant . Different isotopologues of the same molecule produce distinct sets of rotational lines, each with slightly different spacings. If multiple isotopes are present in the sample, the resulting spectrum may show clusters or duplications of lines, corresponding to each isotopologue.
Together, these effects lead to a rotational spectrum that is richer and more complex than the idealised, evenly spaced series of lines predicted by the rigid rotor model.