The spectral decomposition (also known as eigendecomposition or diagonalisation) of an operator is the transformation of an operator in a given basis to one in another basis, such that the resultant operator is represented by a diagonal matrix.
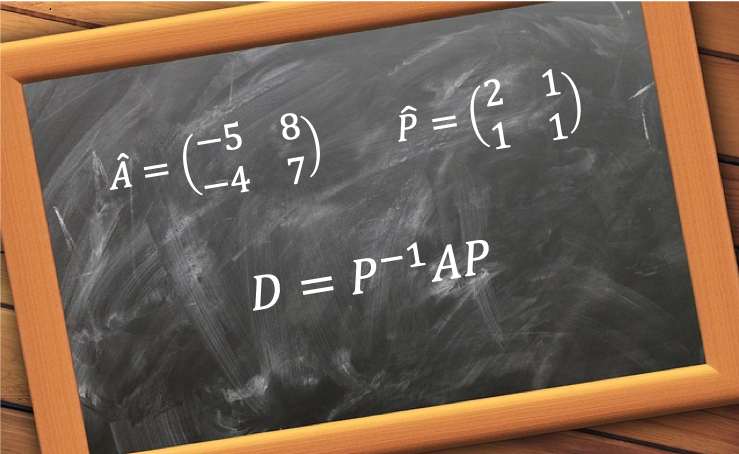
There are 2 main reasons for diagonalising an operator, especially a Hermitian operator. One is to find its eigenvalues and the other is to convert it into a form that is easier to multiply with.

Question
What is a spectrum with respect to linear algebra?
Answer
A spectrum is a collection of all eigenvalues of a matrix. If the matrix represents an operator, its spectral decomposition transforms it to a diagonal matrix with the eigenvalues as its diagonal elements.
Consider an operator with a complete set of orthonormal eigenvectors that is represented by the eigenvalue equation
, where
and
are eigenvalues of
. Since the eigenvectors form a complete set, any vector
can be written as a linear combination of the basis eigenvectors:
where is the coefficient of the basis eigenvector.
Letting act on eq28,
. As we have a complete set of orthonormal eigenvectors,
and
. Furthermore,
is a scalar and matrix multiplication is associative. Therefore,
and
We call eq30 the spectral decomposition of . Since
is the projection operator onto the eigenspace corresponding to
, we can say that the spectral decomposition of a quantum operator represents the operator as a sum of projections onto its eigenstates, weighted by its eigenvalues.

Question
Show that in eq30, where
, is represented by a diagonal matrix.
Answer
Each is a diagonal element of the operator, as well as an eigenvalue of the operator.
In other words, any operator can be expressed in the form of a diagonal matrix if it has the following properties:
-
- Eigenvectors of the operator form a complete set, i.e. the eigenvectors span the vector space.
- Eigenvectors of the operator are orthogonal or can be chosen to be orthogonal.
If the eigenvalues of are real,
This implies that a Hermitian operator can also be expressed in the form of a diagonal matrix because the properties of a Hermitian matrix are:
-
- Eigenvectors of the operator form a complete set, i.e. the eigenvectors span the vector space.
- Eigenvectors of the operator are orthogonal or can be chosen to be orthogonal.
- Eigenvalues of the operator are real.
.
