- Mono Mole

August 6, 2025August 12, 2025

Effect of nuclear statistics on rotational states

The study of nuclear statistics plays a crucial role in understanding the rotational states of atomic nuclei, particularly in systems composed of identical particles, for example, homonuclear diatomic molecules.

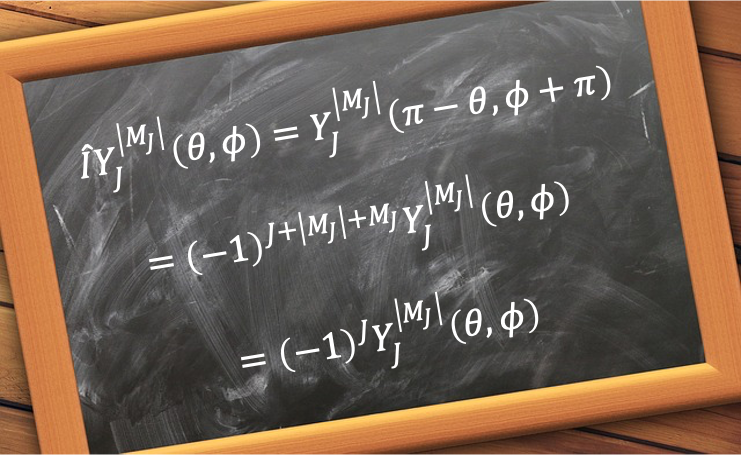
Nuclear statistics dictate which rotational states are populated for molecules with identical nuclei. This effect arises due to a postulate of quantum mechanics, which states that the total wavefunction of a molecule must be either symmetric or antisymmetric with respect to the exchange of identical nuclei, depending on whether the nuclei are bosons or fermions. Such a statistical constraint directly influences the observed spectroscopic transitions.

To understand how nuclear statistics constrain rotational states, we refer to the total wavefunction $\psi_{total}$ for a rotating molecule, which can be approximated as a product of its component wavefunctions:

$\psi_{total}=\psi_{nuc}\psi_{rot}\psi_{vib}\psi_{elec}$

where

$\psi_{nuc}$ is the nuclear spin wavefunction
$\psi_{rot}$ is the rotational wavefunction
$\psi_{vib}$ is the vibrational wavefunction
$\psi_{elec}$ is the electronic wavefunction

Consider the total ground state wavefunction of ¹⁶O₂, where each nucleus is a boson. There are two unpaired electrons occupying separate degenerate antibonding molecular orbitals, while the remaining (core) electrons occupy doubly filled orbitals in singlet states.

The total two-electron wavefunction describing each doubly occupied molecular orbital (MO) is:

$\Psi(1,2)=\frac{1}{\sqrt{2}}\[\phi(1)\phi(2)\chi_{singlet}-\phi(2)\phi(1)\chi_{singlet}\]$

Under a nuclear exchange, $\phi(1)$ and/or $\phi(2)$ may change sign, depending on how the MO transforms under symmetry operations. However their product $\phi(1)\phi(2)$ remains unchanged, so the contribution of each doubly occupied MO to the total wavefunction is symmetric with respect to nuclear exchange.

The molecular orbitals of the two unpaired electrons (triplet state) are formed from the atomic orbitals 2p_x and 2p_y of the oxygen atoms. Since the triplet spin wavefunction is symmetric under electron exchange, the associated spatial part of the wavefunction must be antisymmetric, in accordance with the Pauli exclusion principle:

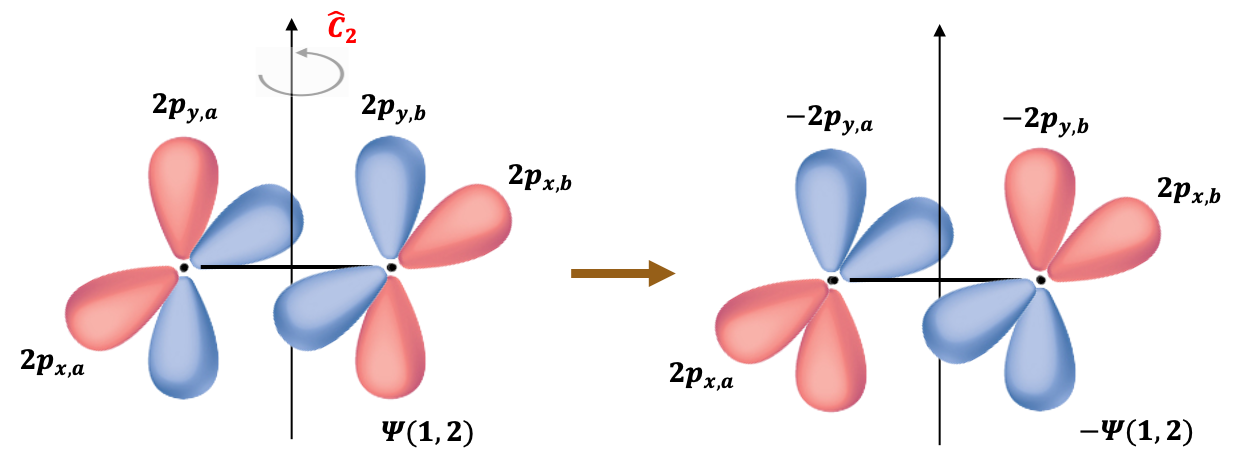
$\Psi(1,2)=\frac{1}{\sqrt{2}}\[\phi_x(1)\phi_y(2)-\phi_y(1)\phi_x(2)\]$

When subject to a rotation operation $\hat{C}_2$ about the principal rotation axis perpendicular to the molecular $z$ -axis (see above diagram),

$\hat{C}_2\Psi(1,2)=\frac{1}{\sqrt{2}}\{\phi_x(1)\[-\phi_y(2)\]-\[-\phi_y(1)\]\phi_x(2)\}=-\Psi(1,2)$

It follows that the valence electronic wavefunction is antisymmetric with respect to this symmetry operation, which corresponds to nuclear exchange in the molecular frame. Therefore, the total ground state electronic wavefunction of ¹⁶O₂, approximated as the product of the core and valence contributions, is antisymmetric under nuclear exchange.

With regard to eq97, the total vibrational ground state wavefunction of ¹⁶O₂ is totally symmetric under all symmetry operations of the molecular point group, since these operations leave the squares of the normal coordinates invariant.

The nuclear spin wavefunction for ¹⁶O₂is given by $\vert\psi\rangle=\vert 0\rangle_1\otimes\vert 0\rangle_2$ (see this article for details), where each ¹⁶O nucleus has zero spin. Since both nuclear spin states are identical, i.e. $\vert 0\rangle_1\equiv\vert 0\rangle_2$ , swapping the subscripts results in the exact same wavefunction. Therefore, the nuclear spin wavefunction is symmetric under nuclear exchange.

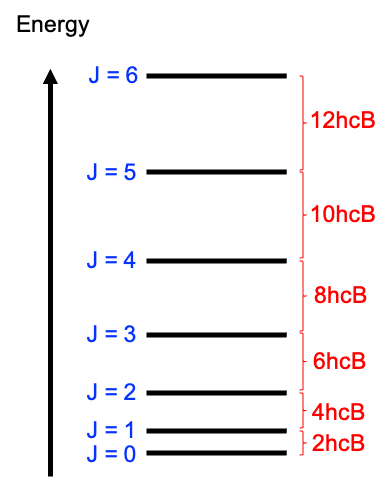
Rotational wavefunctions are represented by spherical harmonics $\vert J,M_J\rangle$ , where the symmetry under nuclear exchange depends on the value of $J$ . These wavefunctions are symmetric for even $J$ and antisymmetric for odd $J$ , i.e. they change sign by $(-1)^J$ under an inversion. Since the total wavefunction of ¹⁶O₂ must be symmetric, half of the possible rotational states are forbidden by nuclear statistics. In other words, ¹⁶O₂ can only occupy odd rotational states in its ground electronic configuration.

Question

Prove that the rotational wavefunction of a diatomic molecule is symmetric for even $J$ and antisymmetric for odd $J$ .

Answer

With reference to eq400, the unnormalised rotational wavefunction of a diatomic molecule is:

$Y_J^{\vert M_J\vert}(\theta,\phi)=P_J^{\vert M_J\vert}(cos\theta)e^{iM_J\phi}$

where $P_J^{\vert M_J\vert}(cos\theta)=\frac{1}{2^JJ!}(1-cos^2\theta)^{\frac{\vert M_J\vert}{2}}\frac{d^{J+\vert M_J\vert}}{d(cos\theta)^{J+\vert M_J\vert}}(cos^2\theta-1)^J$ .

The general and most comprehensive way to analyse the symmetry of a rotational wavefunction is to subject it to an inversion. In spherical coordinates, the inversion operator $\hat{I}$ transforms a position vector from $(\theta,\phi)$ to $(\pi-\theta,\phi+\pi)$ , where the polar angle $\theta$ is reflected about the equatorial plane and the azimuthal angle $\phi$ is rotated by $\pi$ . Since $cos(\pi-\theta)=-cos\theta$ , it follows that

$P_J^{\vert M_J\vert}\[cos(\pi-\theta)\]=\frac{1}{2^JJ!}(1-cos^2\theta)^{\frac{\vert M_J\vert}{2}}\frac{d^{J+\vert M_J\vert}}{d(-cos\theta)^{J+\vert M_J\vert}}(cos^2\theta-1)^J$

Letting $u=cos\theta$ and using the chain rule $\frac{d}{d(-u)}=\frac{d}{du}\frac{du}{d(-u)}$ gives $\frac{d}{d(-cos\theta)}=-\frac{d}{d(cos\theta)}$ , and hence $\frac{d^{J+\vert M_J\vert}}{d(-cos\theta)^{J+\vert M_J\vert}}=(-1)^{J+\vert M_J\vert}\frac{d^{J+\vert M_J\vert}}{d(cos\theta)^{J+\vert M_J\vert}}$ . Furthermore, $e^{iM_J(\phi+\pi)}=e^{iM_J\phi}e^{iM_J\pi}$ , where $e^{iM_J\pi}=(e^{i\pi})^{M_J}=(-1)^{M_J}$ . So, $e^{iM_J(\phi+\pi)}=(-1)^{M_J}e^{iM_J\phi}$ . Therefore,

$\hat{I}Y_J^{\vert M_J\vert}(\theta,\phi)=Y_J^{\vert M_J\vert}(\pi-\theta,\phi+\pi)=(-1)^{J+\vert M_J\vert+M_J}Y_J^{\vert M_J\vert}(\theta,\phi)$

Since $\vert M_J\vert+M_J$ is always even, the wavefunction is symmetric with respect to inversion for even $J$ and antisymmetric for odd $J$ .

While nuclear statistics do not affect the value of the rotational energy levels, they can result in diminished spectral intensities or even “missing” peaks, particularly in Raman spectroscopy. However, this restriction does not apply to heteronuclear diatomic molecules, since the nuclei are not identical and there is no exchange symmetry requirement.

Question

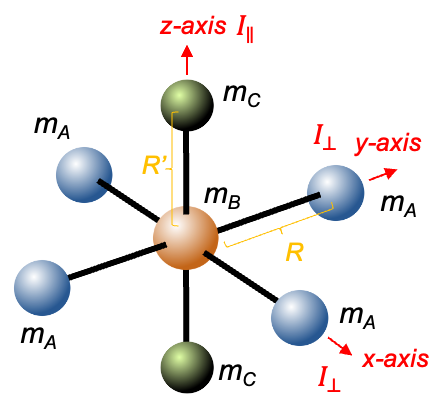
How do nuclear statistics constrain rotational energy levels of ground state symmetrical linear polyatomic molecules like CO₂?

Answer

The principles for analysing nuclear spin statistics in CO₂ are similar to those for O₂. $\psi_{elec}$ , $\psi_{total}$ and $\psi_{nuc}$ must be symmetric under nuclear exchange, which involves two oxygen nuclei in a closed-shell molecule. The ground state vibrational wavefunction of CO₂ is also given by eq97, which is symmetric under nuclear exchange. Therefore, CO₂ can only occupy even rotational states in its ground electronic and vibrational configuration.

Next article: rotational selection rules

Previous article: Molecular rotational energies

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

August 3, 2025August 4, 2025

Particle in a box

A particle in a box is a mathematical model used to illustrate the key principles of quantum mechanics in a simplified system involving the particle moving freely within the box.

1-D box

Consider the case of a free particle of mass $m$ moving between $x=0$ and $x=a$ , where $a> 0$ , along the $x$ -axis of a one-dimensional box. Since a free particle is under the influence of no potential energy, we set $V(x)=0$ in eq44 to give

$-\frac{\hbar^{2}}{2m}\frac{\partial^{2}}{\partial x^{2}}\psi(x)=E\psi(x)\;\;\;\;\;\;\;\;45a$

where the boundary conditions impose the restriction $\psi(0)=\psi(a)=0$ such that the probability of finding the particle $\vert\psi(x)\vert^2$ outside the box is zero.

The general non-trivial solution of eq45a is $\psi(x)=Asinkx+bcoskx$ , where $A$ and $B$ are non-zero constants. Applying the first boundary condition $\psi(0)=0$ , $B$ must be zero, which results in the specific solution $\psi(x)=Asinkx$ . Imposing the second boundary condition $\psi(a)=0$ , we have $\psi(a)Asinka=0$ . This implies that $ka=n\pi$ , where $n=1,2,\cdots$

Question

Can $n$ be zero or negative?

Answer

If $n=0$ , then $k=0$ , and $\psi(x)=Asin(0)=0$ for all $x$ . This would mean that the probability of finding the particle anywhere within the box is zero, which is not a physically meaningful solution. Negative values of $n$ would give the same probability density as positive values of $n$ . Therefore, including negative integers for $n$ would not yield any new, physically distinct solutions. The set of positive integers $n=1,2,\cdots$ is sufficient to describe all possible states of the particle in the box.

It follows that the wavefunction for a particle in a 1-D box is

$\psi(x)=Asin\frac{n\pi x}{a}\;\;\;\;\;\;\;\;45b$

Solving eq45a using eq45b yields:

$E_n=\frac{n^2h^2}{8ma^2}\;\;\;\;n=1,2,\cdots\;\;\;\;45c$

Eq45c shows that the energy of the particle is quantised, with $n$ being the quantum number.

Question

Normalise the wavefunction in eq45b.

Answer

$\int_0^a\psi^*(x)\psi(x)dx=A^2\int_0^asin^2\frac{n\pi x}{a}dx=1$

Setting $u=\frac{n\pi x}{a}$ , with $du=\frac{n\pi}{a}dx$ , and noting that $sin^2u=\frac{1-cos2u}{2}$ , gives

$A^2\frac{a}{n\pi}\int_0^{n\pi}\frac{1-cos2u}{2}du=1$

Therefore, $A=\sqrt{\frac{2}{a}}$ and $\psi(x)=\sqrt{\frac{2}{a}}sin\frac{n\pi x}{a}$ .

3-D box

For a three-dimensional box of lengths $a$ , $b$ and $c$ , the Hamiltonian is given by eq45. Similarly, we set $V(x,y,z)=0$ , resulting in:

$-\frac{\hbar^{2}}{2m}\biggr$\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}\biggr$\psi(x)=E\psi(x)\;\;\;\;\;\;\;\;45d$

Since the motion of the particle in the box along each axis is independent, we can approximate the wavefunction as a product of three functions, each depending on one of the independent coordinates $x$ , $y$ and $z$ :

$\Psi(x,y,z)=\psi_1(x)\psi_2(y)\psi_3(z)\;\;\;\;\;\;\;\;45e$

Using the separation of variables method, we substitute eq45e into eq45d and divide through by eq45e to yield:

$-\frac{\hbar^{2}}{2m\psi_1(x)}\frac{\partial^{2}\psi_1(x)}{\partial x^{2}}-\frac{\hbar^{2}}{2m\psi_2(y)}\frac{\partial^{2}\psi_2(y)}{\partial y^{2}}-\frac{\hbar^{2}}{2m\psi_3(z)}\frac{\partial^{2}\psi_3(z)}{\partial z^{2}}\psi(x)=E\;\;\;\;\;\;\;\;45f$

Since $x$ , $y$ and $z$ are independent variables, the value of each term on RHS of eq45f varies independently, each producing a constant corresponding to the energy in that dimension, with the sum equaling $E$ , i.e. $E_x+E_y+E_z=E$ . In other words, eq45f can be solved by evaluating the following three equations separately:

$-\frac{\hbar^{2}}{2m\psi_1(x)}\frac{\partial^{2}\psi_1(x)}{\partial x^{2}}=E_x$

$-\frac{\hbar^{2}}{2m\psi_2(y)}\frac{\partial^{2}\psi_2(y)}{\partial x^{2}}=E_y$

$-\frac{\hbar^{2}}{2m\psi_3(z)}\frac{\partial^{2}\psi_3(z)}{\partial x^{2}}=E_z$

The respective boundary conditions are

$\psi_1(0)=\psi_1(a)=0\;\;\;\forall y,z$

$\psi_2(0)=\psi_2(b)=0\;\;\;\forall x,z$

$\psi_3(0)=\psi_3(c)=0\;\;\;\forall x,y$

Therefore, the expressions for the three wavefunctions can be derived using the same logic as for the 1-D case, giving:

$\psi_1(x)=\sqrt{\frac{2}{a}}sin\frac{n_x\pi x}{a}\;\;\;\;n_x=1,2,\cdots$

$\psi_2(y)=\sqrt{\frac{2}{b}}sin\frac{n_y\pi y}{b}\;\;\;\;n_y=1,2,\cdots$

$\psi_3(z)=\sqrt{\frac{2}{c}}sin\frac{n_z\pi z}{c}\;\;\;\;n_z=1,2,\cdots$

with

$\Psi(x,y,z)=\sqrt{\frac{8}{abc}}sin\frac{n_x\pi x}{a}sin\frac{n_y\pi y}{b}sin\frac{n_z\pi z}{c}\;\;\;\;\;\;\;\;45g$

and

$E_{n_xn_yn_z}=\frac{h^2}{8m}\biggr$\frac{n_x^2}{a^2}+\frac{n_y^2}{b^2}+\frac{n_z^2}{c^2}\biggr$\;\;\;\;n_x,n_y,n_z=1,2,\cdots\;\;\;\;45h$

Since the energy of a particle moving in a 1-D (or 3-D) box is purely kinetic, eq45c (or eq45h) describes the translational energy of that particle in the box. In general, the wavefunction and energy equations of a particle in 1-D and 3-D boxes have applications in testing the validity of the position and momentum operators, as well as in perturbation theory and statistical thermodynamics.

Next article: one-particle, time-independent schrodinger equation in spherical coordinates

Previous article: one-particle, time-independent schrodinger equation

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

August 1, 2025August 11, 2025

Centrifugal distortion

Centrifugal distortion refers to the deformation of a molecule’s structure that occurs due to the rotational motion of the molecule.

As a molecule rotates, the centrifugal force, which acts outward from the axis of rotation, causes the molecule’s bond lengths and bond angles to stretch and distort, particularly at higher rotational speeds. This effect is most pronounced in larger, heavier molecules, where the rotational energy is sufficient to cause a noticeable shift in the geometry. Centrifugal distortion is an important factor in molecular spectroscopy, as it can influence the rotational energy levels of a molecule, leading to shifts in the observed spectral lines, and must be accounted for when interpreting high-resolution rotational spectra.

What is centrifugal force, and how is it different from centripetal force?

Centripetal force and centrifugal force are both associated with circular motion, but they are described in different frames of reference. Centripetal force is described in an inertial frame of reference or in a frame where the object is experiencing actual physical forces that are measurable and observable. In the inertial frame, the force that keeps the object in circular motion is real and necessary to counteract the object’s tendency to move in a straight line (due to inertia).

Consider a particle moving around a circle (see diagram above) of radius $r$ with an instantaneous velocity $v_1$ at $t=t$ and $v_2$ at $t=t'$ , where $\vert v_1\vert=\vert v_2\vert=v$ . If $\Delta\theta$ is small, the arc length $\Delta s$ is approximately equal to $\Delta r$ and hence to $\Delta v$ . Since the ratio of corresponding sides of two similar triangles is always equal, $\frac{\Delta v}{v}=\frac{\Delta s}{r}$ . Dividing both sides of this equation by $\Delta t$ and rearranging (noting that $a=\frac{\Delta v}{\Delta t}$ and $v=\frac{\Delta s}{\Delta t}$ ) gives:

$a=\frac{v^2}{r}\;\;\;\;\;\;\;\;85$

Substituting $v=r\omega$ (see this article for details) into eq85 yields:

$a=r\omega^2\;\;\;\;\;\;\;\;86$

Therefore the centripetal force $F$ acting on the rotating particle of reduced mass $\mu$ is

$F=\mu r\omega^2\;\;\;\;\;\;\;\;87$

Centrifugal force, on the other hand, is experienced in a non-inertia frame of reference (rotating frame). It appears to act outward on the rotating particle. However, it does not correspond to any real physical force but is instead a fictitious force introduced to account for the observed effects of acceleration in the rotating frame. Since the magnitude of centrifugal force is the same as that of the centripetal force, the magnitude of the centrifugal force experienced by a diatomic molecule of reduced mass $\mu$ and bond length $r$ rotating at angular velocity $\omega$ is $\mu r\omega^2$ .

At equilibrium, the centrifugal force equals the restoring force given by Hooke’s law:

$\mu r\omega^2=k(r-r_0)\;\;\;\;\;\;\;\;88$

where $k$ is the force constant and $r_0$ is the equilibrium bond length.

For small displacements, the motion expressed by eq88 is simple harmonic, with the following classical Hamiltonian for the system:

$H=\frac{J^2}{2\mu r^2}+\frac{1}{2}k(r-r_0)^2\;\;\;\;\;\;\;\;89$

where the kinetic energy term is given by the classical form of eq4a and the potential energy term is derived from this article.

Rearranging eq88 results in $r=\frac{1}{1-\mu\omega^2/k}r_0$ , and therefore

$\frac{1}{r^2}=\frac{1}{r_0^2}-\frac{2\mu\omega^2}{kr^2_0}+\frac{\mu^2\omega^4}{k^2r^2_0}\;\;\;\;\;\;\;\;90$

For small displacements, $r\approx r_0$ , which implies from $r=\frac{1}{1-\mu\omega^2/k}r_0$ that $1-\frac{\mu\omega^2}{k}\approx 1$ , and hence $\vert\frac{\mu\omega^2}{k}\vert\ll 1$ . So, we can ignore the last term in eq90 as a first approximation, giving:

$\frac{1}{r^2}=\frac{1}{r_0^2}-\frac{2\mu\omega^2}{kr^2_0}\;\;\;\;\;\;\;\;91$

Substituting $J=I\omega=\mu r^2\omega$ (see this article for details) into RHS of eq91 gives:

$\frac{1}{r^2}=\frac{1}{r_0^2}-\frac{2J^2}{k\mu r^4r^2_0}\;\;\;\;\;\;\;\;92$

Substituting eq92 and eq88 into eq89 yields:

$H=\frac{J^2}{2\mu r_0^2}-\frac{J^4}{k\mu^2r^4r_0^2}+\frac{J^4}{2k\mu^2 r^6}\;\;\;\;\;\;\;\;93$

Since $r\approx r_0$ for small displacements, eq93 becomes:

$H=\frac{J^2}{2\mu r_0^2}-\frac{J^4}{2k\mu^2r_0^6}$

Using the quantum mechanics postulate that “to every observable quantity in classical mechanics there corresponds a linear, Hermitian operator in quantum mechanics”, and replacing the classical angular momentum $J$ with the quantum mechanical operator gives

$\hat{H}=\frac{\hat{J}^2}{2\mu r_0^2}-\frac{\hat{J}^4}{2k\mu^2r_0^6}\;\;\;\;\;\;\;\;94$

The corresponding eigenvalues of eq94 (derived using orbital angular momentum ladder operators) are:

$E=\frac{J(J+1)\hbar^2}{2\mu r_0^2}-\frac{J^2(J+1)^2\hbar^4}{2k\mu^2r_0^6}$

$E=hcBJ(J+1)-hcDJ^2(J+1)^2\;\;\;\;\;\;\;\;95$

where $B=\frac{\hbar}{4\pi c\mu r_0^2}$ is the rotational constant and $D=\frac{\hbar^3}{4\pi ck\mu^2r_0^6}$ is the centrifugal distortion constant.

However, rotational energies are typically reported as wavenumbers in molecular spectroscopy. Substituting $E=h\nu$ and $c=\nu\lambda$ into eq95 yields $\tilde{\nu}=BJ(J+1)-DJ^2(J+1)^2$ , which is a function of $J$ . Therefore,

$F(J)=BJ(J+1)-DJ^2(J+1)^2\;\;\;\;\;\;\;\;96$

Previous article: Microwave spectra

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

August 1, 2025August 5, 2025

Microwave spectra

Microwave spectra represent the electromagnetic radiation absorbed or emitted by molecules when they undergo transitions between discrete rotational energy levels. These spectra are a key component in the study of molecular structure and dynamics. They provide valuable insights about molecular properties, such as bond lengths and moments of inertia.

An ideal pure rotational spectrum of a rigid linear molecule, generated in the microwave frequency range of 10¹¹ to 10¹² Hz, typically exhibits a series of absorption lines that correspond to the rotational transitions of the molecule between discrete rotational energy levels (see diagram below). In the absence of an external magnetic field, these transitions follow the selection rule $\Delta J-\pm 1$ , meaning that a molecule can only transition between adjacent rotational levels.

The rotational energy levels are given by eq44 or eq45 and the frequencies of the transitions are directly related to the rotational constant $B$ , and as such, the spacing between the spectral lines provides information about the moment of inertia and the molecular structure. Using the definition $\tilde{\nu}=BJ(J+1)$ , we have

$\tilde{\nu}=B[(J+1)(J+2)-J(J+1)]=2B(J+1)\;\;\;\;\;\;\;\;80$

Therefore, the first peak, obtained by substituting $J=0$ into eq80, lies at the point $2B$ along the horizontal axis. Similarly, the second and third peaks are at $4B$ and $6B$ respectively. In other words, the peaks in an ideal rotational spectrum (without centrifugal distortion) of a rigid linear rotor are equally spaced at $2B$ .

Question

Calculate the moment of inertia and bond length of HCl if the line spacing in the rotational spectrum is 21.2 cm^-1?

Answer

Since the spacing is $2B$ , we have $B=10.6$ cm^-1. Using the formula $B=\frac{\hbar}{4\pi cI}$ gives $I=2.64\times 10^{-47}$ kg m². Furthermore, $I=\mu r^2=\biggr$\frac{35.5}{1+35.5}\biggr$\frac{1\times 10^{-3}}{N_A}r^2$ . Therefore, the bond length is $r=1.28\times 10^{-10}$ m.

The intensity of each transition $J\rightarrow J+1$ depends on the population of the initial level $J$ , which is governed by the Boltzmann distribution, with higher- $J$ states being less populated at lower temperatures:

$\frac{n_J}{N}=\frac{e^{-\frac{\varepsilon_J}{kT}}}{\sum_Je^{-\frac{\varepsilon_J}{kT}}}$

where

$k$ is the Boltzmann constant.
$n_J$ is the number of particles in the energy state $\varepsilon_J$ .
$N$ is the total number of particles in the system.

Since $\frac{n_j}{N}$ represents the fraction of particles in the state $\varepsilon_J$ , the intensity of a spectral line is proportional to $e^{-\frac{\varepsilon_J}{kT}}$ , where the value $\varepsilon_J$ corresponds to a specific energy level. However, there are $(2J+1)$ degenerate states associated with each value of $J$ in a rigid linear molecule. This degeneracy increases the statistical weight of higher $J$ levels, redistributing the population towards more degenerate states, which become thermally accessible at typical laboratory temperatures. In other words, at a given temperature, more particles will occupy a higher $J$ state with greater degeneracy at equilibrium than they would if the state were non-degenerate. Therefore, when a sample is exposed to an external microwave field, the intensity $I$ of each allowed transition in the pure rotational spectrum is proportional to the population of the initial state, which is the product of $e^{-\frac{\varepsilon_J}{kT}}$ and $(2J+1)$ . This gives:

$I=N'(2J+1)e^{-\frac{hcBJ(J+1)}{kT}}\;\;\;\;\;\;\;\;81$

where $N'$ is a proportionality constant and $\varepsilon_J$ is given by eq45.

The factor $(2J+1)$ in eq81 increases linearly with $J$ , while the exponential term decreases exponentially. As a result, the graph of $I$ versus $J$ forms a skewed bell curve (see diagram above), with a maximum found by treating $J$ as a continuous variable and taking the derivative of $I$ with respect to $J$ :

$\frac{dI}{dJ}=N'e^{-\frac{hcBJ(J+1)}{kT}}\biggr\[2-(2J+1)^2\frac{hcB}{kT}\biggr\]$

Setting $\frac{dI}{dJ}=0$ , and noting that $e^{-\frac{hcBJ(J+1)}{kT}}\neq 0$ for any finite $J$ , gives

$J=\sqrt{\frac{kT}{2hcB}}-\frac{1}{2}\;\;\;\;\;\;\;\;82$

Since $J$ must be an integer, the maximum intensity occurs at the value of $J$ closest to the result of eq82.

Question

Is the intensity of each transition dependent on the electric dipole moment?

Answer

Although the transition probability between adjacent rotational states is proportional to $\vert\langle\psi(\theta,\phi)_{l',m'_l}\vert\boldsymbol{\mathit{\hat{\mu}}}\vert\psi(\theta,\phi)_{l,m_l}\rangle\vert^2$ , which depends on the magnitude of the electric dipole moment, the sample molecules in the waveguide of a typical microwave spectrometer are randomly oriented. As a result, the effect transition dipole moment does not vary significantly from one $J\rightarrow J+1$ transition to the next for a given molecule. Therefore, while the absolute intensity depends on the dipole moment, it is often treated as a constant factor when comparing transitions within the same molecule.

For a symmetric rotor, $\tilde{\nu}=\tilde{B}J(J+1)+K^2(\tilde{A}-\tilde{B})$ and $\Delta\tilde{\nu}$ is also given by eq80. However, the spectrum is not just a single series of equally spaced lines like that of a linear rotor. Instead, each value of $\tilde{\nu}=K$ is associated with a series of lines with equal spacing of $2\tilde{B}$ . In other words, a symmetric top spectrum consists of multiple superimposed series of equally spaced lines, each corresponding to a different value of $K$ . As a result, the individual lines may not be as clearly resolved and may appear as a denser pattern compared to that of a linear molecule. Nevertheless, the overall intensity envelope of the spectrum still resembles a skewed bell curve, with the maximum intensity occurring at the $J$ value where the population is highest.

In practice, the peaks in a real rotational spectrum are not vertical lines but have finite width and shape, appearing as broadened curves. This broadening arises, under typical laboratory conditions, from several effects:

- Doppler broadening, due to the thermal motion of molecules, causes a spread in observed frequencies as molecules move towards or away from the detector.
- Instrumental broadening results from the finite resolution of the spectrometer itself.

Beyond broadening, other phenomena affect the detailed structure and spacing of the spectral lines:

- Centrifugal distortion causes deviations from the ideal rigid rotor model. As rotational speed increases with higher $J$ levels, the molecular bond stretches slightly, increasing the moment of inertia and decreasing the rotational constant $B$ . This leads to uneven spacing between lines, especially at higher $J$ , and is accounted for using a correction term.

- Isotopic substitution alters the moment of inertia due to the change in atomic mass, thereby changing the rotational constant $B$ . Different isotopologues of the same molecule produce distinct sets of rotational lines, each with slightly different spacings. If multiple isotopes are present in the sample, the resulting spectrum may show clusters or duplications of lines, corresponding to each isotopologue.

Together, these effects lead to a rotational spectrum that is richer and more complex than the idealised, evenly spaced series of lines predicted by the rigid rotor model.

Next article: Centrifugal distortion

Previous article: Microwave spectroscopy (instrumentation)

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

August 1, 2025

Microwave spectroscopy (Instrumentation)

Microwave spectroscopy is a powerful analytical technique that analyses the rotational transitions of molecules. Operating in the microwave region of the electromagnetic spectrum, this method provides highly precise information about molecular structure, bond lengths, bond angles, and even the distribution of electrons within a molecule.

The diagram above outlines a conventional microwave spectrometer. A stable and tunable microwave source is essential for probing molecular energy transitions. This is fulfilled by a device known as a Klystron amplifier, which is a vacuum tube engineered to generate and amplify narrow-band microwave signals that can be precisely tuned to the desired frequency. It was invented in 1937 by American electrical engineers Russell and Sigurd Varian.

A Klystron amplifier includes an electron gun, two resonant cavities (buncher and catcher), a drift tube and a collector (see diagram above). The electron gun operates on the principle of thermionic emission, where electrons are emitted from a heated coil (cathode) and accelerated towards an anode. The buncher cavity is connected to a weak external AC supply (with frequency in the microwave range), which creates an oscillating flow of free electrons within the cavity walls. This, in turn, generates an alternating electric field across the perforated section (grid) of the cavity.

As electrons pass through the grid, they are either accelerated or decelerated depending on the polarity of the electric field. When the entrance grid is negative and the exit grid is positive, electrons are accelerated. When the polarity reverses, they are decelerated. This periodic acceleration and deceleration causes the electrons to bunch together as they travel through the drift tube, forming dense clusters that correspond to the frequency of the external AC source.

When these bunched electrons enter the catcher cavity, they induce a stronger alternating current (due to their higher density) at the same frequency as the AC input. Through an inductor, this energy is converted into strong monochromatic microwave radiation, which is then propagated along a waveguide.

Question

Is the frequency of the generated microwave radiation tunable? How does induction occur in the catcher cavity?

Answer

The resonant cavities are precisely engineered in both shape and size to resonate at a narrow band of microwave frequencies. Each Klystron amplifier module has a narrow operational bandwidth that can be tuned by mechanically adjusting the cavity dimensions using tuning screws. To cover a wider frequency range, multiple modules with different cavity dimensions must be employed.

Electromagnetic theory states that a flowing current generates a magnetic field, and that a changing magnetic field induces an alternating current in a conductor. The varying density of electrons flowing through the catcher cavity constitutes a varying current, which in turn creates a time-varying magnetic field. This results in the induction of an alternating current within the cavity walls.

The waveguide, constructed using copper of stainless steel, is a hollow evacuated tube designed to confine and direct the microwaves to the sample cell, which is often a section of the waveguide. Gases to be analysed are introduced via a gas inlet system, and the cell is often equipped with pumps and valves to control pressure and flush previous samples.

If the monochromatic microwave radiation matches the energy of a specific rotational transition of the molecules, a portion of it will be absorbed by the sample. The remaining (transmitted) microwave signal then reaches the detector, which typically consists of an inductive pickup (antenna), a diode rectifier, capacitors, and an amplifier. The inductor acts as an antenna that couples the microwave radiation into an alternating current (AC), which is then rectified by the diode to produce a pulsating direct current (DC) signal. A low-pass filter, often just a capacitor, smooths the rectified signal into a more stable DC voltage. This process is repeated as the microwave frequency is swept or incremented across a range. At each frequency step, the resulting DC voltage, which is proportional to the transmitted microwave intensity, is amplified and sent to a computer for data acquisition and analysis. Finally, the amplitudes of the DC voltages are plotted as a function of frequency, producing a microwave absorption spectrum that reveals the rotational transitions of the sample.

Next article: Microwave spectra

Previous article: rotational selection rules

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

August 1, 2025August 6, 2025

Rotational selection rules

Rotational selection rules for molecules determine the probabilities of rotational state transitions observed in spectroscopy.

According to the time-dependent perturbation theory, the transition probability $\vert\mu_{fi}\vert^2$ between the orthogonal rotational states $\psi(\theta,\phi)_{l,m_l}$ and $\psi(\theta,\phi)_{l',m'_l}$ within a given vibrational state of a molecule, as observed by microwave spectroscopy, is proportional to $\vert\langle\psi(\theta,\phi)_{l',m'_l}\vert\boldsymbol{\mathit{\hat{\mu}}}\vert\psi(\theta,\phi)_{l,m_l}\rangle\vert^2$ , where $\boldsymbol{\mathit{\hat{\mu}}}$ is the operator for the molecule’s electric dipole moment. In other words, a molecule must possess a permanent electric dipole moment ( $\boldsymbol{\mathit{\hat{\mu}}}\neq 0$ ) to exhibit a rotational spectrum. Homonuclear diatomic molecules and spherical rotors with no net permanent dipole moment (such as H₂ and CH₄ in their ground states) are generally rotationally inactive.

Since $\boldsymbol{\mathit{\hat{\mu}}}=\boldsymbol{\mathit{i}}\hat{\mu}_x+\boldsymbol{\mathit{j}}\hat{\mu}_y+\boldsymbol{\mathit{k}}\hat{\mu}_z$ , the components of the dipole moment in polar coordinates are:

$\hat{\mu}_x=\mu sin\theta cos\phi\;\;\;\;\;\;\;\;60$

$\hat{\mu}_y=\mu sin\theta sin\phi\;\;\;\;\;\;\;\;61$

$\hat{\mu}_z=\mu cos\theta\;\;\;\;\;\;\;\;62$

Suppose the perturbation on the molecule is caused by a plane-polarised electromagnetic wave with an electric component $\varepsilon_z$ oscillating in the $z$ -direction. We have $\vert\mu_{z,fi}\vert^2\propto\vert\langle\psi(\theta,\phi)_{l',m'_l}\vert\hat{\mu_z}\vert\psi(\theta,\phi)_{l,m_l}\rangle\vert^2$ , with

$\mu_{z,fi}=\int_0^{\pi}\int_0^{2\pi}\psi^*(\theta,\phi)_{l',m'_l}\mu cos\theta\psi(\theta,\phi)_{l,m_l}sin\theta d\theta d\phi\;\;\;\;\;\;\;\;63$

Substituting the explicit expression of the spherical harmonics wavefunction $\psi(\theta,\phi)$ into eq63 gives:

$\mu_{z,fi}=\mu N'N\int_0^{\pi}cos\theta P_{l'}^{\vert m'_l\vert}P_l^{\vert m_l\vert}sin\theta d\theta\int_0^{2\pi}e^{i(m_l-m'_l)\phi}d\phi\;\;\;\;\;\;\;\;64$

where $N'N=\frac{1}{2\pi}\biggr\[\biggr$\frac{2l'+1}{2}\biggr$\frac{(l'-\vert m'_l\vert)!}{(l'+\vert m'_l\vert)!}\biggr\]^{\frac{1}{2}}\biggr\[\biggr$\frac{2l+1}{2}\biggr$\frac{(l-\vert m_l\vert)!}{(l+\vert m_l\vert)!}\biggr\]^{\frac{1}{2}}$ , and $P_{l'}^{\vert m'_l\vert}$ and $P_{l}^{\vert m_l\vert}$ are functions of $cos\theta$ .

When $m_l\neq m'_l$ , the integral with respect to $\phi$ is $\int_0^{2\pi}e^{i(m_l-m'_l)\phi}d\phi =0$ . When $m_l=m'_l$ , it evaluates to $\int_0^{2\pi}e^{i(m_l-m'_l)\phi}d\phi =2\pi$ . Since eq63 must be non-zero for a transition to be probable in the $z$ -direction, $m_l=m'_l$ or

$\Delta m_l=0\;\;\;\;\;\;\;\;65$

Substituting $\int_0^{2\pi}e^{i(m_l-m'_l)\phi}d\phi =2\pi$ back into eq64 and noting that $d(cos\theta)=-sin\theta d\theta$ yields:

$\mu_{z,fi}=\mu N''\int_{-1}^{1}cos\theta P_{l'}^{\vert m'_l\vert}P_l^{\vert m_l\vert}d(cos\theta)\;\;\;\;\;\;\;\;66$

where $N''=\frac{1}{2}\biggr\[\frac{(2l'+1)(2l+1)(l'-\vert m'_l\vert)!(l-\vert m_l\vert)!}{(l'+\vert m'_l\vert)!(l+\vert m_l\vert)!}\biggr\]^{\frac{1}{2}}$ .

Substituting the polar coordinate form $x=cos\theta$ into eq370 (a recurrence relation of the associated Legendre polynomials) results in:

$cos\theta P_{l}^{\vert m_l\vert}=\frac{l+\vert m_l\vert}{2l+1}P_{l-1}^{\vert m_l\vert}+\frac{l-\vert m_l\vert+1}{2l+1}P_{l+1}^{\vert m_l\vert}\;\;\;\;\;\;\;\;67$

Substituting eq67 into eq66 gives:

$\mu_{z,fi}=\mu N''\biggr\[\frac{l+\vert m_l\vert}{2l+1}\int_{-1}^{1}P_{l'}^{\vert m'_l\vert}P_l^{\vert m_l\vert}d(cos\theta)+\frac{l-\vert m_l\vert+1}{2l+1}\int_{-1}^{1}P_{l'}^{\vert m'_l\vert}P_l^{\vert m_l\vert}d(cos\theta)\biggr\]\;\;\;\;\;\;\;\;68$

For $\mu_{z,fi}\neq 0$ , either integral in eq68 must be non-zero. Each integral is non-zero when the corresponding pair of spherical harmonics is not orthogonal. This occurs if $l'=l-1$ and $m'_l=m_l$ for the first integral and $l'=l+1$ and $m'_l=m_l$ for the second integral. In other words, $\mu_{z,fi}\neq 0$ if

$\Delta l=\pm 1\;\;\;\;and\;\;\;\;\Delta m_l=0$

or using rotational spectroscopy notations:

$\Delta J=\pm 1\;\;\;\;and\;\;\;\;\Delta M_J=0\;\;\;\;\;\;\;\;69$

For an electric component $\varepsilon_x$ oscillating in the $x$ -direction, eq63 becomes

$\mu_{x,fi}=\int_0^{\pi}\int_0^{2\pi}\psi^*(\theta,\phi)_{l',m'_l}\mu sin\theta cos\phi\psi(\theta,\phi)_{l,m_l}sin\theta d\theta d\phi\;\;\;\;\;\;\;\;70$

Substituting the explicit expression of the spherical harmonics wavefunction $\psi(\theta,\phi)$ and $cos\phi=\frac{e^{i\phi}+e^{-i\phi}}{2}$ into eq70 gives:

$\mu_{x,fi}=\frac{\mu}{2}N'N\int_0^{\pi}sin\theta P_{l'}^{\vert m'_l\vert}P_l^{\vert m_l\vert}sin\theta d\theta\int_0^{2\pi}[e^{i(m_l-m'_l+1)\phi}+e^{i(m_l-m'_l-1)\phi}] d\phi\;\;\;\;\;\;\;\;71$

When $m'_l=m_l$ , the integral with respect to $\phi$ equals zero. When $m_l\pm 1=m'_l$ , it evaluates to $2\pi$ . Since eq71 must be non-zero for a transition to be probable in the $x$ -direction, it must satisfy:

$\Delta m_l=\pm 1\;\;\;\;\;\;\;\;72$

Substituting $\int_0^{2\pi}[e^{i(m_l-m'_l+1)\phi}+e^{i(m_l-m'_l-1)\phi}] d\phi=2\pi$ back into eq71, and noting that $d(cos\theta)=-sin\theta d\theta$ , yields:

$\mu_{x,fi}=\frac{\mu}{2}N''\int_{-1}^{1}sin\theta P_{l'}^{\vert m_l\pm 1\vert}P_l^{\vert m_l\vert} d(cos\theta)\;\;\;\;\;\;\;\;73$

Substituting the polar coordinate form $x=cos\theta$ and into eq371 (another recurrence relation of the associated Legendre polynomials) results in:

$sin\theta P_{l}^{\vert m_l\vert}=\frac{1}{2l+1}P_{l+1}^{\vert m_l\vert+1}-\frac{1}{2l+1}P_{l-1}^{\vert m_l\vert+1}\;\;\;\;\;\;\;\;74$

Substituting eq74 into eq73 gives:

$\mu_{x,fi}=\frac{\mu N''}{2(2l+1)}\biggr\[\int_{-1}^{1}P_{l'}^{\vert m_l\pm 1\vert}P_{l+1}^{\vert m_l\vert+1} d(cos\theta)-\int_{-1}^{1}P_{l'}^{\vert m_l\pm 1\vert}P_{l-1}^{\vert m_l\vert+1} d(cos\theta)\biggr\]\;\;\;\;\;\;\;\;75$

For $\mu_{x,fi}\neq 0$ , either integral in eq75 must be non-zero. Each integral is non-zero when the corresponding pair of spherical harmonics is not orthogonal. This occurs if

Integrals	Condition 1	Cases	Condition 2	Results
1^st	$l'=l+1$	$m_l+1=m'_l$	$\vert m_l+1\vert-\vert m_l\vert=+1$	$\Delta m_l=+1$ if $m_l\geq 0$
		$m_l+1=m'_l$	$\vert m_l\vert-\vert m_l+1\vert=-1$	$\Delta m_l=-1$ if $m_l\geq 0$
		$m_l-1=m'_l$	$\vert m_l-1\vert-\vert m_l\vert=+1$	$\Delta m_l=+1$ if $m_l\leq 0$
		$m_l-1=m'_l$	$\vert m_l\vert-\vert m_l-1\vert=-1$	$\Delta m_l=-1$ if $m_l\leq 0$
2^nd	$l'=l-1$	$m_l+1=m'_l$	$\vert m_l+1\vert-\vert m_l\vert=+1$	$\Delta m_l=+1$ if $m_l\geq 0$
		$m_l+1=m'_l$	$\vert m_l\vert-\vert m_l+1\vert=-1$	$\Delta m_l=-1$ if $m_l\geq 0$
		$m_l-1=m'_l$	$\vert m_l-1\vert-\vert m_l\vert=+1$	$\Delta m_l=+1$ if $m_l\leq 0$
		$m_l-1=m'_l$	$\vert m_l\vert-\vert m_l-1\vert=-1$	$\Delta m_l=-1$ if $m_l\leq 0$

Combining the results, $\mu_{x,fi}\neq 0$ when $\Delta l=\pm 1$ and $\Delta m_l=\pm 1$ , or in rotational spectroscopy notations:

$\Delta J=\pm 1\;\;\;\;and\;\;\;\;\Delta M_J=\pm 1\;\;\;\;\;\;\;\;76$

Repeating the derivation for $\mu_{y,fi}$ , we arrive at the same selection rules expressed by eq76. Therefore, the rotational selection rules for polar molecules (linear rotors and spherical rotors) subjected to isotropic radiation are:

$\Delta J=\pm 1\;\;\;\;and\;\;\;\;\Delta M_J=0,\pm 1\;\;\;\;\;\;\;\;77$

For symmetric rotors, the electric dipole moment lies along the principal molecular axis ( $z$ -axis). However, there is a third quantum number $K$ to consider. The wavefunction $\psi(J,M_J,K)$ can be approximated as the product of three functions $f_1f_2f_3$ , where $f_3=e^{-iK\gamma}$ depends solely on the quantum number $K$ . If $\hat{\mu}_{z}$ in the matrix element $\langle J'M'K'\vert\hat{\mu}_{z}\vert JMK\rangle$ is defined with respect to the molecular axis, then the matrix element can be expressed as a product of three integrals, one of which is $\int f_3'^*(K)\hat{\mu}_{z}f_3(K)d\gamma$ . For this integral to be non-zero, the vanishing integral theorem from group theory states that $\hat{\mu}_{z}$ must transform as the totally symmetric irreducible representation of the molecule’s point group (which is the case in $C_{nv}$ groups) and $K'=K$ . In other words, the rotational transition selection rules for symmetric rotors are:

$\Delta J=\pm 1,\;\;\;\;\Delta M_J=0,\pm 1\;\;\;\;and\;\;\;\;\Delta K=0\;\;\;\;\;\;\;\;78$

Question

Is the effect of nuclear statistics on rotational states different from rotational selection rules?

Answer

The effect of nuclear statistics on rotational states is a separate, yet related, concept from the general rotational selection rules. While both influence which rotational states are observed in a spectrum, they operate based on different fundamental principles. The key distinction is that rotational selection rules dictate the possible transitions, while nuclear statistics determine the relative populations of the initial states. A transition must be both “allowed” by the selection rules and originate from a “populated” state to be observed. Therefore, nuclear statistics modify the intensity of the allowed transitions without changing the fundamental rule of which transitions are allowed.

Next article: Microwave spectroscopy (Instrumentation)

Previous article: Effect of nuclear statistics on rotational states

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

August 1, 2025August 6, 2025

Molecular rotational energies

Molecular rotational energies are quantised states arising from rotation about principal axes, determined by the moments of inertia. These levels are fundamental in molecular spectroscopy.

Diatomic rigid rotor

For a diatomic rigid rotor, the rotational Hamiltonian is given by eq4a, $\hat{H}_{rot}=\frac{\hat{J}^2}{2I}$ . Here, $\hat{J}^2$ is the square of the total angular momentum operator, with the eigenvalues $J(J+1)\hbar^2$ (derived using orbital angular momentum ladder operators), where $J=0,1,2,\cdots$ is the rotational quantum number and $\hbar=\frac{h}{2\pi}$ . Therefore, the rotational energy levels of a diatomic molecule are given by:

$E=J(J+1)\frac{\hbar^2}{2I}\;\;\;\;\;\;\;\;44$

Eq44 can also be expressed in terms of the rotational constant $B=\frac{\hbar}{4\pi cI$ :

$E=hcBJ(J+1)\;\;\;\;\;\;\;\;45$

where $h$ is the Planck constant and $c$ is the speed of light.

However, rotational energies are typically reported as wavenumbers in molecular spectroscopy. Substituting $E=h\nu$ and $c=\nu\lambda$ into eq45 yields $\tilde{\nu}=BJ(J+1)$ , which is a function of $J$ . Therefore,

$F(J)=BJ(J+1)\;\;\;\;\;\;\;\;46$

This indicates that the separation between adjacent rotational levels increases linearly with $J$ (see above diagram), as given by:

$F(J)-F(J-1)=2BJ\;\;\;\;\;\;\;\;47$

Furthermore, each energy level (i.e. eq44 for a particular value of $J$ ) is $(2J+1)$ -fold degenerate due to the allowed eigenvalues of the $z$ –component of angular momentum, which are $M_J\hbar$ , where $M_J=-J,-J+1,\cdots,J$ . In the absence of an external magnetic field, these sublevels are degenerate.

Other linear rotors

A rigid linear triatomic molecule (e.g. HCN) behaves similarly as a diatomic rigid rotor when rotating about an axis perpendicular to its bond axis. The moment of inertia about the molecular axis is essentially zero due to the absence of perpendicular mass displacement. Therefore, the rotational energy levels are, per eq44:

$E=J(J+1)\frac{\hbar^2}{2I}\;\;\;\;or\;\;\;\;F(J)=BJ(J+1)$

where $I$ is given by eq15.

Similar to diatomic molecules, each $E$ is $(2J+1)$ -fold degenerate in the absence of an external magnetic field.

Question

Is C₂H₂ also a linear rotor?

Answer

Yes. Its rotational energy levels are also given by eq44 and eq46.

Symmetric rotors

Symmetric rotors have two equal moments of inertia $I_{\perp}$ about mutually orthogonal axes. Each of these is perpendicular to a third rotational axis associated with a distinct, non-zero moment of inertia $I_{\parallel}$ . If $I_{\parallel}< I_{\perp}$ , the molecule is known as a prolate symmetric rotor (shaped like a cigar) and rotates more easily around the principal axis. Examples include NH₃ and CHCl₃. If $I_{\parallel}> I_{\perp}$ , the molecule is called an oblate symmetric rotor (flattened like a disc), and it rotates more easily around an axis perpendicular to the disc. Examples include C₆H₆ and BF₃.

The rotational Hamiltonian of a rigid symmetric rotor in the molecule-fixed frame is given by eq4d:

$\hat{H}_{rot}=\frac{\hat{J}_x^2}{2I_x}+\frac{\hat{J}_y^2}{2I_y}+\frac{\hat{J}_z^2}{2I_z}$

Conventionally, $I_x=I_y=I_z$ and $I_z=I_{\parallel}$ . Furthermore, from eq75, $\hat{J}^2=\hat{J}^2_x+\hat{J}^2_y+\hat{J}^2_z$ . Therefore,

$\hat{H}_{rot}=\frac{\hat{J}_x^2+\hat{J}_y^2}{2I_{\perp}}+\frac{\hat{J}_z^2}{2I_{\parallel}}=\frac{\hat{J}^2}{2I_{\perp}}+\hat{J}^2_z\biggr$\frac{1}{2I_{\parallel}}-\frac{1}{2I_{\perp}}\biggr$\;\;\;\;\;\;\;\;48$

With reference to eq132, and replacing the notations $\hat{L}_z$ , $l$ and $m_l$ with $\hat{J}_z$ , $J$ and $K$ , where $K=-J,-J+1,-J+2,\cdots,J$ , we have $\hat{J}^2_z\psi=\hat{J}_z(\hat{J}_z\psi)=K^2\hbar^2\psi$ . It follows that the rotational energy levels of a rigid symmetric rotor are given by:

$E=J(J+1)\frac{\hbar^2}{2I_{\perp}}+K^2\hbar^2\biggr$\frac{1}{2I_{\parallel}}-\frac{1}{2I_{\perp}}\biggr$\;\;\;\;\;\;\;\;49$

Question

Is $K$ a quantum number? Is it the same as $m_l$ ?

Answer

In eq48, $\hat{J}_z$ refers to the component of the angular momentum operator along the symmetry axis (or $z$ -axis) in the molecule-fixed frame, not the $z$ -axis in the laboratory frame. Although its eigenvalues have the same form as those of $\hat{J}_z$ in the laboratory frame, it is a different quantum number from $m_l$ (or $M_J$ ). An analogy can be made with the projections of the spin vector of a spinning top: its projection along its own axis differs in general from the projection along an arbitrary laboratory axis, unless the axes are aligned. While both projections can take similar ranges of values (assuming these values are quantised), they are not equal in general. Likewise, $K$ and $M_J$ are related to projections in different frames and are different quantum numbers.

Substituting $\tilde{A}=\frac{\hbar}{4\pi cI_{\parallel}$ and $\tilde{B}=\frac{\hbar}{4\pi cI_{\perp}$ into eq49 yields:

$E=hc\tilde{B}J(J+1)+K^2hc(\tilde{A}-\tilde{B})\;\;\;\;\;\;\;\;50$

Substituting $E=h\nu$ and $c=\nu\lambda$ into eq50 gives $\tilde{\nu}=\tilde{B}J(J+1)+K^2(\tilde{A}-\tilde{B})$ , which is a function of two rotational quantum numbers $J$ and $K$ . Therefore,

$F(J,K)=\tilde{B}J(J+1)+K^2(\tilde{A}-\tilde{B})\;\;\;\;\;\;\;\;51$

When $K=0$ , there is only one distinct moment of inertia, with eq51 reducing to eq46, where $\tilde{B}=B$ . In this case, each $E$ is $(2J+1)$ -fold degenerate in the absence of an external magnetic field. If $K\neq 0$ , $E$ is determined by the magnitudes of $J$ and $K^2$ . Since $E$ is the same for $(+K)^2$ and $(-K)^2$ for each $J$ in eq49, the energy levels for $+K$ and $-K$ are degenerate. Additionally, there are $2J+1$ possible $M_J$ substates for each value of $J$ . Therefore, the total degeneracy when $K\neq 0$ is $2(2J+1)$ in the absence of an external magnetic field.

Spherical rotors

A spherical rotor has three equal moments of inertia $I_x=I_y=I_z=I$ about three mutually orthogonal axes. It belongs to a point group that is a parent group of that of a symmetric rotor. Therefore, the rotational energy levels of a spherical rotor can be described by eq49 with $I_{\parallel}=I_{\perp}$ , which is equivalent the condition $\tilde{A}=\tilde{B}$ in eq50. This implies that $E$ remains a function of both $J$ and $K$ , and that for a given energy level, $K$ is not restricted to just two values (as in the case of a symmetric rotor), but can take on $2J+1$ different values. It follows that each energy level is $(2J+1)^2$ -fold degenerate in the absence of an external magnetic field.

Next article: Effect of nuclear statistics on rotational states

Previous article: Moments of inertia of spherical rotors

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

August 1, 2025

Moments of inertia of spherical rotors

A spherical rotor is a molecule in which the moments of inertia about all three principal axes are equal. This high degree of symmetry, typically found in molecules with tetrahedral (e.g. methane, CH₄), octahedral (e.g. sulfur hexafluoride, SF₆), or icosahedral geometries, leads to simplified rotational behaviour. Unlike asymmetric or symmetric rotors, spherical rotors exhibit degenerate energy levels due to their identical rotational constants along each axis. As a result, they serve as important models in quantum mechanics and spectroscopy, particularly for interpreting rotational spectra and understanding molecular symmetry.

The left diagram above shows an octahedral molecule of the type BA₆( $O_h$ symmetry), where B is the central atom. The moment of inertia along the $z$ -axis, which is equal to those along the $x$ -axis and $y$ -axis, is $I=\sum_{i=1}^4m_ir_i^2=\sum_{i=1}^4m_i(x_i^2+y_i^2)$ or

$I=4m_AR^2\;\;\;\;\;\;\;\;40$

Question

Why do the three atoms that lie along the $z$ -axis not contribute to $I$ ?

Answer

In general, $I=\sum_{i=1}^Nm_ir_i^2=\sum_{i=1}^Nm_i(x_i^2+y_i^2+z_i^2)$ . Since the three atoms along the rotational axis, the moment of inertia about this axis is effectively zero due to the absence of perpendicular mass displacement ( $z_i=0$ ).

To determine the moment of inertia of the tetrahedral molecule around the $z$ -axis, let atom B be at the centre of a cube (see diagram above), which is designated as the origin $(0,0,0)$ . The four A atoms ( $A_1$ , $A_2$ , $A_3$ and $A_4$ ) are located at alternating vertices, with coordinates: $A_1(k,k,k)$ , $A_2(k,-k,-k)$ , $A_3(-k,k,-k)$ and $A_4(-k,-k,k)$ , where $k$ is the half the length of an edge of the cube.

Since the B-A bond length is $R$ , we have $R=\sqrt{k^2+k^2+k^2}$ , which when substituted back into the coordinates yields: $A_1(\frac{R}{\sqrt{3}},\frac{R}{\sqrt{3}},\frac{R}{\sqrt{3}})$ , $A_2(\frac{R}{\sqrt{3}},-\frac{R}{\sqrt{3}},-\frac{R}{\sqrt{3}})$ , $A_3(-\frac{R}{\sqrt{3}},\frac{R}{\sqrt{3}},-\frac{R}{\sqrt{3}})$ and $A_4(-\frac{R}{\sqrt{3}},-\frac{R}{\sqrt{3}},\frac{R}{\sqrt{3}})$ . Therefore, the moment of inertia of the tetrahedral molecule around the $z$ -axis is:

$I=\sum_{i=1}^4m_i(x_i^2+y_i^2)=\frac{8}{3}m_AR^2\;\;\;\;\;\;\;\;41$

Next article: Molecular rotational energies

Previous article: Moments of inertia of a trigonal planar oblate symmetric rotor with D_3h symmetry

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

August 1, 2025

Moments of inertia of a trigonal planar oblate symmetric rotor with $D_{3h}$ symmetry

The moments of inertia of a trigonal planar oblate rotor with $D_{3h}$ symmetry (e.g. BF₃) are characterised by a unique moment of inertia $I_{\parallel}$ around the principal axis and two equal moments of inertia $I_{\perp}$ perpendicular to the principal axis, where $I_{\parallel}>I_{\perp}$ . They are derived using simple geometric considerations.

The diagram above shows a trigonal planar oblate rotor with its centre of mass located at atom B (of mass $m_B$ ), which is positioned at the origin $(0,0,0)$ . The three A atoms (1,2 and 3), each with mass $m_A$ , are equally spaced at 120° apart on an imaginary circle of radius $R$ .

The moment of inertia along the $z$ -axis, which is perpendicular to the plane of the diagram, is $I_{\parallel}=\sum_{i=1}^3m_ir_i^2=\sum_{i=1}^3m_i(x_i^2+y_i^2)$ . Since the three B-A bonds have equal lengths of $R$ , we have

$I_{\parallel}=3m_AR^2\;\;\;\;\;\;\;\;38$

Question

Why do $m_B$ not contribute to $I_{\parallel}$ ?

Answer

In general, $I_{\parallel}=\sum_{i=1}^Nm_ir_i^2=\sum_{i=1}^Nm_i(x_i^2+y_i^2+z_i^2)$ . Since atom B lie along the rotational axis, the moment of inertia about this axis is effectively zero due to the absence of perpendicular mass displacement ( $z_i=0$ ).

To derive $I_{\perp}$ , we can make use of the coordinates of the atoms that form the base of a trigonal pyramidal molecule mentioned in an earlier article, where $m_B=0$ and $\phi=90\degree$ :

Atom	Coordinates
Atom	Trigonal pyramidal	Trigonal planar
A₁	$\biggr$Rsin\phi,0,-\frac{m_BRcos\phi}{3m_A+m_B}\biggr$$	$(R,0,0)$
A₂	$\biggr$-\frac{1}{2}Rsin\phi,\frac{\sqrt{3}}{2}Rsin\phi,-\frac{m_BRcos\phi}{3m_A+m_B}\biggr$$	$\biggr$-\frac{1}{2}R,\frac{\sqrt{3}}{2}R,0\biggr$$
A₃	$\biggr$-\frac{1}{2}Rsin\phi,-\frac{\sqrt{3}}{2}Rsin\phi,-\frac{m_BRcos\phi}{3m_A+m_B}\biggr$$	$\biggr$-\frac{1}{2}R,-\frac{\sqrt{3}}{2}R,0\biggr$$

Therefore, $I_{\perp,y}=\sum_{i=1}^2m_ix_i^2$ or

$I_{\perp}=\frac{3}{2}m_AR^2\;\;\;\;\;\;\;\;39$

Similarly, $I_{\perp,x}=\frac{3}{2}m_AR^2$ .

Next article: Moments of inertia of spherical rotors

Previous article: Moments of inertia of octahedral prolate symmetric rotor with D_4h symmetry

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

August 1, 2025

Moments of inertia of octahedral prolate symmetric rotor with $D_{4h}$ symmetry

The moments of inertia of an octahedral prolate rotor with $D_{4h}$ symmetry (e.g. Pt(NH₃)₂Cl₄) are characterised by a unique moment of inertia $I_{\parallel}$ around the principal axis and two equal moments of inertia $I_{\perp}$ perpendicular to the principal axis, where $I_{\parallel}<I_{\perp}$ . They are derived using simple geometric considerations.

The diagram above shows an octahedral molecule of the type BA₄C₂, where B is the central atom. The moment of inertia along the $z$ -axis is $I_{\parallel}=\sum_{i=1}^4m_ir_i^2=\sum_{i=1}^4m_i(x_i^2+y_i^2)$ . Since the four B-A bonds have equal lengths of , we have

$I_{\parallel}=4m_AR^2\;\;\;\;\;\;\;\;35$

Question

Why do $m_B$ and $m_C$ not contribute to $I_{\parallel}$ ?

Answer

In general, $I_{\parallel}=\sum_{i=1}^Nm_ir_i^2=\sum_{i=1}^Nm_i(x_i^2+y_i^2+z_i^2)$ . Since atoms B and C lie along the rotational axis, the moment of inertia about this axis is effectively zero due to the absence of perpendicular mass displacement ( $z_i=0$ ).

Similarly, the moment of inertia of the molecule about the $x$ -axis, which is equal to that about the $y$ -axis, is $I_{\perp}=\sum_{i=1}^4m_i(y_i^2+z_i^2)$ . Since the two B-C bonds have equal lengths of $R'$ , we have

$I_{\perp}=2m_AR^2+2m_CR'^2\;\;\;\;\;\;\;\;36$

You’ll find that the expression for the moment of inertia about the $y$ -axis is the same as eq36.

Question

Answer

Question

Answer

Next article: rotational selection rules

Previous article: Molecular rotational energies

Question

Answer

Question

Answer

Next article: one-particle, time-independent schrodinger equation in spherical coordinates

Previous article: one-particle, time-independent schrodinger equation

Previous article: Microwave spectra

Question

Answer

Question

Answer

Next article: Centrifugal distortion

Previous article: Microwave spectroscopy (instrumentation)

Question

Answer

Next article: Microwave spectra

Previous article: rotational selection rules

Question

Answer

Next article: Microwave spectroscopy (Instrumentation)

Previous article: Effect of nuclear statistics on rotational states

Question

Answer

Question

Answer

Next article: Effect of nuclear statistics on rotational states

Previous article: Moments of inertia of spherical rotors

Question

Answer

Next article: Molecular rotational energies

Previous article: Moments of inertia of a trigonal planar oblate symmetric rotor with D3h symmetry

Question

Answer

Next article: Moments of inertia of spherical rotors

Previous article: Moments of inertia of octahedral prolate symmetric rotor with D4h symmetry

Question

Answer

Next article: Moments of inertia of a trigonal planar oblate symmetric rotor with D3h symmetry

Previous article: Moments of inertia of tetrahedral prolate symmetric rotor with C3v symmetry

Previous article: Moments of inertia of a trigonal planar oblate symmetric rotor with D_3h symmetry

Previous article: Moments of inertia of octahedral prolate symmetric rotor with D_4h symmetry

Next article: Moments of inertia of a trigonal planar oblate symmetric rotor with D_3h symmetry

Previous article: Moments of inertia of tetrahedral prolate symmetric rotor with C_3v symmetry