A subgroup is a collection of elements within a larger group that forms its own distinct group. For example, 
is a subgroup of 
(see multiplication table below).
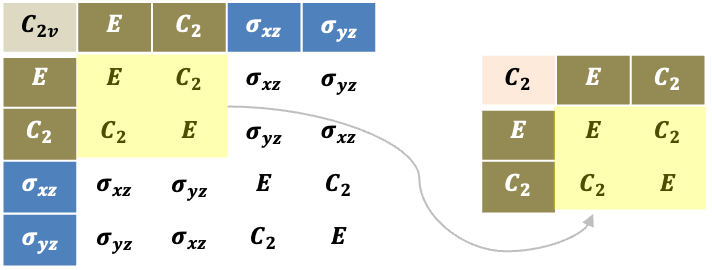
A group is always a subgroup of itself; such a subgroup is called an improper subgroup. Every group has a trivial subgroup, which contains only the identity element. All other subgroups are known as proper subgroups.
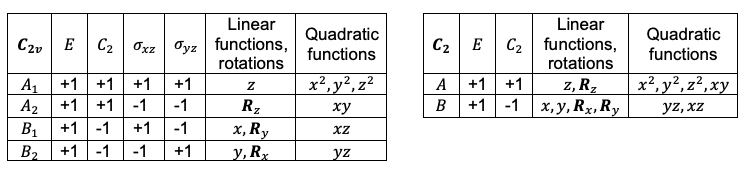
The irreducible representations of the subgroup and its parent group, generated from the same set of basis functions, exhibit identical characters associated with symmetry operations that are common to both groups (see character tables below). This occurs because
A basis function undergoing a specific symmetry operation is associated with the same transformation matrix and, consequently, the same trace in both the subgroup and its parent group.
We say that the representations of a subgroup and its parent group are correlated. For example, 
and 
of the point group are correlated to 
and 
of the 
point group, respectively. The correlation of representations of two point groups can be used to determine the nature of certain properties of a basis function. This is especially relevant when the properties, for instance spin, are independent of the spatial coordinate system and therefore invariant under any symmetry operations. Further explanation can be found in the next article.
Let’s consider a more complicated case: 
and its subgroup 
. When comparing the character tables (see below) of both groups, it becomes evident that the symmetry operations 
and 
of are not preserved in . However, apart from the identity and inversion symmetry operations, the remaining symmetry operations of are partially preserved (e.g. five of the fifteen symmetry operations). To simplify the correlation of irreducible representations between the two groups, we focus on the symmetry operations that are unambiguously preserved. In the descent of symmetry from to , the preserved operations include 
, 
, 
, 
, 
and 
. Consequently, 
, 
, 
and 
of are correlated to , 
, and 
of , respectively.
of does not appear to correlate with any single irreducible representation of . However, there must exist a basis function that transforms according to both of and a representation of . The logic behind this begins with the fact that if a chemical species is invariant under the symmetry operations of a group 
, it is also invariant under the symmetry operations of a subgroup of . Therefore, a basis function that transforms according to an irreducible representation of must also transform to a representation of the subgroup of . Since a basis function associated with of  does not transform according to any irreducible representation of , it must transform according to a reducible representation of .
As mentioned above, a basis function undergoing a specific symmetry operation is associated with the same transformation matrix and, consequently, the same trace in both the subgroup and its parent group. This implies that of  correlates to the  reducible representation that is a direct sum of the irreducible representations 
. Similarly, we have
In summary, a descent in symmetry occurs when a subgroup inherits symmetries from its parent group, preserving certain properties while reducing the overall complexity. It is useful in constructing weak-strong ligand field correlation diagrams.
