Born-Haber cycle (chemical energetics)

The Born-Haber cycle is a method to analyse reaction enthalpies, particularly to calculate the standard enthalpy change of lattice energy, ΔH_latt^o, which cannot be measured precisely via experiments. It is based on Hess’ law and developed by the German scientists Max Born and Fritz Haber in 1916. Born-Haber cycles are best represented in the form of energy diagrams. For example, if we want to calculate the standard enthalpy change of lattice energy of calcium fluoride, we start by writing the equations for ΔH_latt^o[CaF₂(s)] and ΔH_f^o[CaF₂(s)] :

$CaF_2(s)\rightarrow Ca^{2+}(g)+2F^-(g)\; \; \; \; \; \; \; \; \Delta H_{latt}^{\: o}\; \; \; \; \; \; \; \; 7$

$Ca(s)+F_2(g)\rightarrow CaF_2(s)\; \; \; \; \; \; \; \; \Delta H_{f}^{\: o}$

Applying Hess’ law, we can combine the two equations into a cycle:

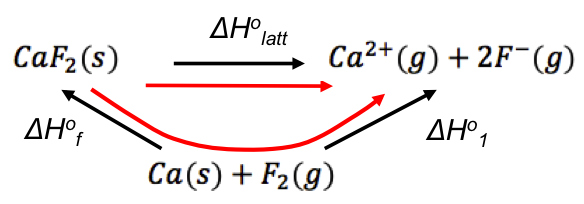
ΔH₁^o is composed of a few standard enthalpy changes. If we rewrite the cycle to include every standard enthalpy change (starting with the reactants of ΔH_f^o), we have the Born-Haber cycle for CaF₂(s):

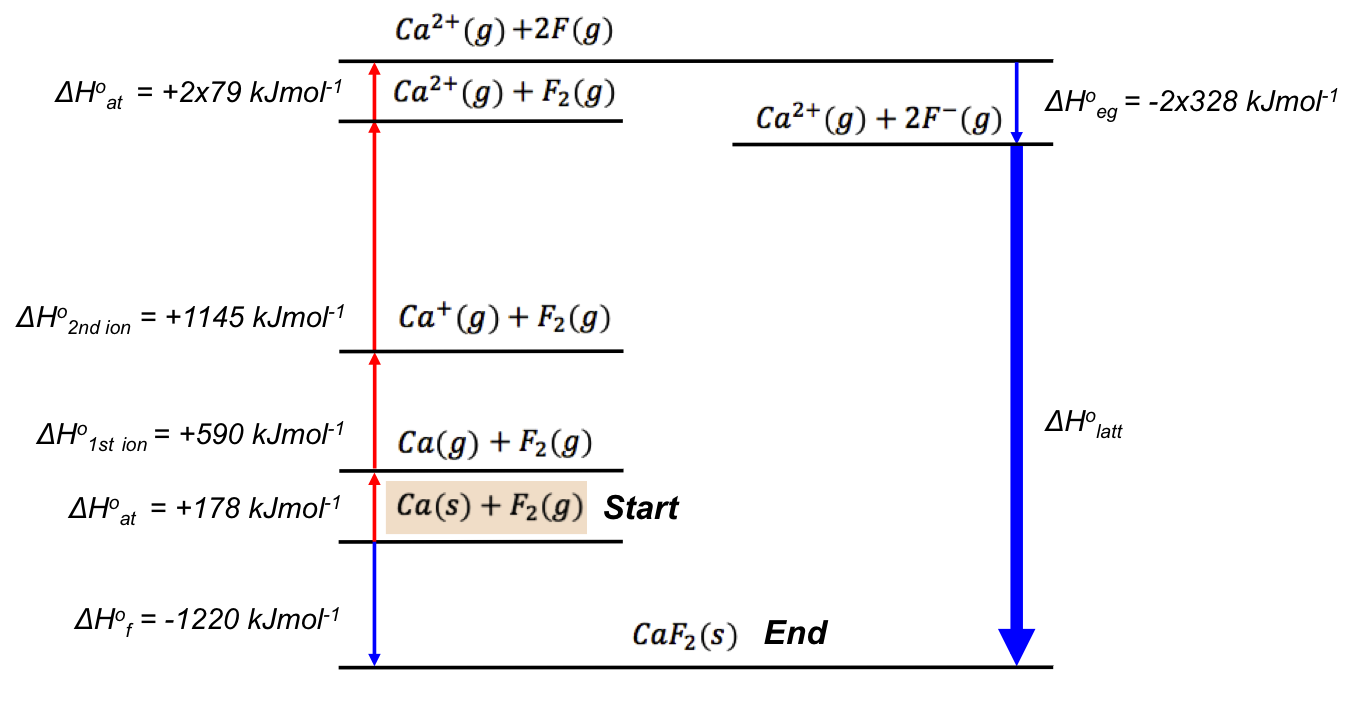
The Born-Haber cycle (also known as the Born-Haber energy diagram) reveals that ΔH₁^o is composed of ΔH^o_at, ΔH^o_{1st ion}, ΔH^o_{2nd ion}, another ΔH^o_at and ΔH^o_eg. It is also evident that the sum of the magnitudes of each enthalpy on the left-hand side of the energy diagram is equal to that on the right-hand side, i.e.

$\Sigma_i\left | \Delta H^o_i\left ( LHS \right ) \right |=\Sigma_j\left | \Delta H^o_j\left ( RHS \right ) \right |$

$\vert -1220\vert+178+590+1145+2(79)=\vert\Delta H_{latt}^{\: o}\vert+\vert -2(328)\vert$

$\vert\Delta H_{latt}^{\: o}\vert=2635\: kJmol^{-1}$

The above computation shows that ΔH^o_lattfor CaF₂can be +2635 kJmol^-1 or -2635 kJmol^-1 depending on its definition. Since we have defined the standard enthalpy change of lattice energy as an endothermic process (see eq7, where ΔH^o_lattis the change in enthalpy to break one mole of a solid ionic compound and separate its gaseous ions to an infinite distance under standard conditions), ΔH_latt^o = +2635 kJmol^-1.

In summary, the steps involved in establishing the Born-Haber cycle are:

1. Write the equations for the standard enthalpy change of lattice energy and the standard enthalpy change of formation of the ionic compound.
2. Combine the two equations into a cycle using Hess’ law.
3. Expand the cycle in a stepwise manner to include every standard enthalpy change.
4. Draw the Born-Haber cycle energy diagram starting with the reactants of the standard enthalpy change of formation of the compound and ending with the ionic compound.
5. Sum the magnitude of enthalpies on each side of the cycle and equate them to find ΔH_latt^o.

Born-Haber cycle (chemical energetics)

Previous article: Hess’s law

Content page of intermediate chemical energetics

Content page of intermediate chemistry

Main content page

Leave a Reply Cancel reply