Canonical partition function

The canonical partition function $Q$ is a statistical sum over all microstates in the canonical ensemble, providing the normalisation needed to determine the probability that each state is occupied in a system in thermal equilibrium at a fixed temperature.

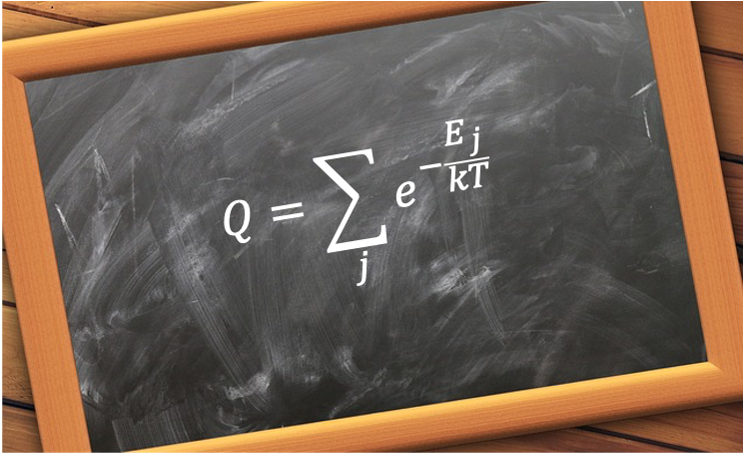
It mathematically given by eq135. To explain why it is called a partition function, we need to evaluate $\beta$ in eq133, which defines the functional form of the probability distribution for a microstate in any system in thermal equilibrium with a heat bath.

Consider a thermal bath in contact with two distinct systems, $a$ and $b$ , where system $a$ has volume $V_a$ and particle number $N_a$ , while system $b$ has a different volume $V_b$ and particle number $N_b$ . The microstates of system $a$ are governed by a constant $\beta_a$ , such that $p_{i,a}\propto e^{-\beta_aE_{i,a}}$ , and those of system $b$ are governed by a constant $\beta_b$ , with $p_{i,b}\propto e^{-\beta_bE_{i,b}}$ . Similarly, the combined system $a+b$ is governed by a single constant, $\beta_{a+b}$ , with the total energy of a microstate for the combined system equal to the sum of the energies of the individual microstates, $E_{a+b}=E_a+E_b$ . According to the derived probability distribution, the probability of a microstate of the combined system is:

$p_{a+b}\propto e^{-\beta_{a+b}(E_a+E_b)}\;\;\;\;\;\;\;\;140$

On the other hand, the probability of finding the combined system in a specific state is also the product of the probabilities of finding each individual system in its corresponding state:

$p_{a+b}\propto p_{a}\cdot p_b\propto e^{-(\beta_aE_a+\beta_bE_b)}\;\;\;\;\;\;\;\;141$

For eq140 and eq141 to be consistent for all possible values of $E_a$ and $E_b$ , we must have $\beta_{a+b}=\beta_a=\beta_b=\beta$ . As explained in the previous article, eq133 is derived under the postulate that all microstates with equal energy have equal probability of occurring in any system with fixed volume, composition and temperature. This implies that $p_i$ , and possibly $\beta$ , may depend on $V$ , $N$ and $T$ . However, the two systems have different $V$ and $N$ , yet share the value of $\beta$ . Therefore, $\beta$ cannot depend on $V$ or $N$ . Since the only parameter common to both systems is the temperature of the thermal bath, $\beta$ can be a function of temperature alone: $\beta=\beta(T)$ .

Question

Explain why $E_i$ is a function of $V$ and $N$ only.

Answer

$E_i$ , the energy corresponding to each microstate, is determined by solving the Schrodinger equation $\hat{H}\psi_i=E_i\psi_i$ , where $\psi_i$ is the wavefunction that describes the quantum state resulting from the positions and momenta of all $N$ particles in the system. Therefore, $E_i$ is a function of $V$ and $N$ only.

Building on the above general argument that $\beta$ is solely a function of temperature, consider the special case of two systems with the same $V$ , $N$ and $T$ , as in the canonical ensemble. Applying the same reasoning here, we again find that the systems share the same $\beta$ , reinforcing that $\beta$ depends only on temperature. Thus, regardless of whether the systems have identical or differing volumes and particle numbers, as long as they are in thermal equilibrium with the same heat bath, $\beta$ is a function solely of temperature, independent of the systems’ internal structure or composition.

To determine the exact expression for $\beta$ , we refer to eq120, which is based on the postulate that the macroscopic properties of a system are given by the ensemble average. In other words, the equation applies to the average of any mechanical property $\langle M\rangle$ :

$M=\langle M\rangle=\sum_ip_iM_i\;\;\;\;\;\;\;\;142$

Consider the system’s pressure $P$ . When we change the volume of the system, the energy $E_i$ associated with a microstate of the system also changes. The work done on the system is $dW=-P_idV$ , where $P_i$ is the pressure contributed by the $i$ -th microstate of the system. Since the work done on the system corresponds to a mechanical change in the system’s internal energy, we can also write $dE_i=-P_idV$ , or equivalently,

$P_i=-\biggr$\frac{\partial E_i}{\partial V}\biggr$_N\;\;\;\;\;\;\;\;143$

Substituting eq143 back into eq142 gives:

$P=-\sum_ip_i\biggr$\frac{\partial E_i}{\partial V}\biggr$_N\;\;\;\;\;\;\;\;144$

Using the chain rule, the partial differentiation of eq135 yields:

$\biggr$\frac{\partial Q}{\partial V}\biggr$_{T,N}=\sum_i\frac{\partial e^{-\beta E_i}}{\partial E_i}\biggr$\frac{\partial E_i}{\partial V}\biggr$_N=-\beta\sum_ie^{-\beta E_i}\biggr$\frac{\partial E_i}{\partial V}\biggr$_N\;\;\;\;\;\;\;\;145$

Substituting eq133 and eq145 into eq144 results in:

$P=\frac{1}{\beta Q}\biggr$\frac{\partial Q}{\partial V}\biggr$_{T,N}=\frac{1}{\beta}\biggr$\frac{\partial lnQ}{\partial V}\biggr$_{T,N}\;\;\;\;\;\;\;\;146$

The partial derivative of $Q$ with respect to $\beta$ is:

$\biggr$\frac{\partial Q}{\partial \beta}\biggr$_{V,N}=-\sum_iE_ie^{-\beta E_i}\;\;\;\;\;\;\;\;147$

Substituting eq147 into eq134 gives:

$U=-\frac{1}{Q}\biggr$\frac{\partial Q}{\partial \beta}\biggr$_{V,N}=-\biggr$\frac{\partial lnQ}{\partial \beta}\biggr$_{V,N}\;\;\;\;\;\;\;\;148$

It follows that:

$\biggr$\frac{\partial U}{\partial V}\biggr$_{T,N}=-\biggr\[\frac{\partial}{\partial V}\biggr$\frac{\partial lnQ}{\partial \beta}\biggr$_{V,N}\biggr\]_{T,N}$

Assuming that the function $lnQ$ is continuous over the domain of interest, we can interchange the derivatives:

$\biggr$\frac{\partial U}{\partial V}\biggr$_{T,N}=-\biggr\[\frac{\partial}{\partial \beta}\biggr$\frac{\partial lnQ}{\partial V}\biggr$_{T,N}\biggr\]_{V,N}\;\;\;\;\;\;\;\;149$

Substituting eq146 into eq149 yields:

$\biggr$\frac{\partial U}{\partial V}\biggr$_{T,N}=-\biggr\[\frac{\partial}{\partial \beta}(\beta P)\biggr\]_{V,N}=-P-\beta\biggr$\frac{\partial P}{\partial \beta}\biggr$_{V,N}\;\;\;\;\;\;\;\;150$

Comparing eq150 with the thermodynamic identity given by eq127 results in:

$-\beta\biggr$\frac{\partial P}{\partial \beta}\biggr$_{V,N}=T\biggr$\frac{\partial P}{\partial T}\biggr$_{V,N}\;\;\;\;\;\;\;\;151$

Using the chain rule $\frac{\partial P}{\partial T}=\frac{\partial P}{\partial (1/T)}\frac{\partial (1/T)}{\partial T}=-\frac{1}{T^2}\frac{\partial P}{\partial (1/T)}$ and substituting it into eq151 gives:

$\beta\biggr$\frac{\partial P}{\partial \beta}\biggr$_{V,N}=\frac{1}{T}\biggr\[\frac{\partial P}{\partial (1/T)}\biggr\]_{V,N}\;\;\;\;\;\;\;\;152$

Substituting $X=\frac{1}{T}$ into eq152 and using the reciprocal identity yields:

$\frac{\beta}{X}=\biggr$\frac{\partial \beta}{\partial P}\biggr$_{V,N}\biggr$\frac{\partial P}{\partial X}\biggr$_{V,N}\;\;\;\;\;\;\;\;153$

Since $\beta$ and $X$ are functions of $T$ only, the chain rule form of eq153 can be simplified to $\frac{\beta}{X}=\frac{d\beta}{dX}$ , or equivalently, $\frac{dX}{X}=\frac{d\beta}{\beta}$ . When integrated, this results in $lnX=ln\beta+C$ , or $X=\beta e^C$ , where $C$ is a constant. Therefore,

$\beta=\frac{1}{kT}\;\;\;\;\;\;\;\;154$

where $k=e^C$ is a constant.

Substituting eq154 back into eq135 gives the explicit form of the canonical partition function:

$Q=\sum_je^{-\frac{E_j}{kT}}\;\;\;\;\;\;\;\;155$

As discussed, the probability of finding a system, which is in thermal equilibrium with a constant temperature heat bath, in a specific microstate $i$ with energy $E_i$ is given by $p_i=\frac{e^{-\beta E_i}}{Q}$ . Here, the numerator represents the unnormalised statistical weight of microstate $i$ . This weight becomes a meaningful probability only after dividing by $Q$ , which represents the total statistical weight of all accessible microstates. In this sense, $Q$ enables the partitioning of the total probability of 1 across all microstates, in proportion to their energy. This is why it is called a partition function.

Canonical partition function

Question

Answer

Next article: thermodynamic functions involving the canonical partition function

Previous article: the Canonical ensemble

Content page of statistical thermodynamics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply