The canonical partition function is a central quantity in statistical mechanics, encapsulating the thermodynamic behaviour of a system in equilibrium with a heat reservoir at fixed temperature. It allows us to derive key thermodynamic quantities of a system, such as pressure (see eq146) and internal energy (see eq148). These relationships, e.g. _{V,N})
, applies to both systems with interacting and non-interacting particles.
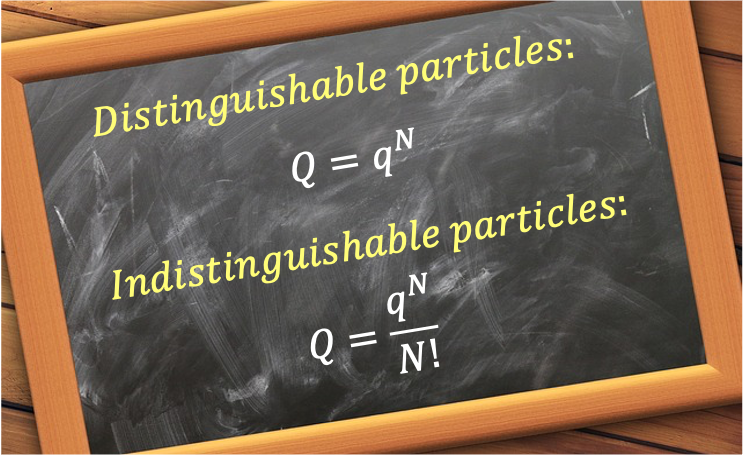
For a system with interacting particles, the Schrödinger equation is incredibly complex due to the interaction terms between the 
particles, making it difficult to calculate the exact energy 
of a given microstate . On the other hand, in a system of non-interacting particles, intermolecular forces are absent. This simplifies the evaluation of 
significantly, since the Hamiltonian operator for a system of non-interacting particles can be expressed as 
. The total energy of the system then becomes the sum of the individual particle energies,
Here 
refers to the energy of particle 1 in quantum state 
when the system is in microstate 
. The energy of each particle is determined by solving the corresponding one-particle Schrödinger equation, e.g. 
.
If the non-interacting particles are distinguishable (e.g. atoms or molecules with fixed positions in a solid), then the microstate of the system is defined by the quantum state of each individual particle. For example, microstate 1 might have the configuration 
, while microstate 2 is 
. The sum over all microstates of the system, by substituting eq160 into eq155, is given by:
which is equivalent to:
where we have set 
and 
for illustrative purposes.
Each term on the RHS of eq161 corresponds to a distinct microstate, represented by a specific permutation of exponential factors. Eq161 can also be written as:
We can show that eq162 is equivalent to eq161 by expanding it:
\biggr\(e^{-\frac{\varepsilon^1_{2,1}}{kT}}+e^{-\frac{\varepsilon^2_{2,2}}{kT}}+\cdots\biggr\)\cdots\;\;\;\;\;\;\;\;163)
If we multiply out all the terms in eq163, each resulting term corresponds to a unique microstate, as expressed in eq161. Therefore,
where 
, 
,…, 
are known as the molecular partition functions.
Since each 
represents the total statistical weight of a single particle, the superscript 
in 
becomes redundant. Thus, we can express a molecular partition function more simply as 
. If 
molecules are of the same species, where 
, then
^{N_1}q_2\cdots q_{N-N_1}\;\;\;\;\;\;\;\;165)
Question
Using the example of a system of 3 distinguishable, identical, non-interacting particles, show that the sum over all microstates of the system then becomes the product of the separate sums of the quantum states of each particle.
Answer
Suppose each particle can be in one of two quantum states with energy 
and 
. The total possible microstates is 
, comprising of:
So,
Similarly,
^3=1+3e^{-\frac{\varepsilon}{kT}}+3e^{-\frac{2\varepsilon}{kT}}+e^{-\frac{3\varepsilon}{kT}})
It follows that for distinguishable, identical, non-interacting particles,
If the identical, non-interacting particles are indistinguishable, such as those of an ideal gas, and if each particle occupies a distinct quantum state, then the total number of microstates is no longer given by the number of permutations of the quantum states, but by the number of combinations. One way to approximate in this case is to divide eq166 by a factor 
:
This gives 
at high temperatures, where each particle is assumed to be in a distinct quantum state. It is important to note that the relation is not a strict mathematical identity, because 
is not a literal count of microstates but a weighted sum of exponential terms, each corresponding to a microstate. Nevertheless, this approximation works well in the classical limit and successfully resolves the Gibbs paradox.