Advanced Chemistry - Mono Mole

July 13, 2022September 26, 2024

Stationary state

A stationary state is described by a wavefunction that is associated with a probability density and an expectation value that are both independent of time.

For the time-independent Schrodinger equation, $\hat{H}\psi =E\psi$ , its solutions are stationary states. This implies that stationary states of the time-independent $\hat{H}$ can be represented by basis wavefunctions but not linear combinations of basis wavefunctions with non-zero coefficients. For example, the wavefunction $\psi\left ( x,t \right )=\phi\left ( x \right )e^{-iEt/\hbar}$ describes a stationary state because:

$\left | \psi\left ( x,t \right ) \right |^{2}=\psi^{*}\psi=\phi^{*}e^{iEt/\hbar}\phi e^{-iEt/\hbar}=\left | \psi\left ( x \right ) \right |^{2}$

and

$\left \langle H \right \rangle=\int \psi^{*}\hat{H}\psi dx=\int \phi^{*}e^{iEt/\hbar}\hat{H}\phi e^{-iEt/\hbar}dx=E\int \phi^{*}\phi dx=E$

whereas $\psi\left ( x,t \right )=\sum_{n=1}^{2}c_n\phi_n\left ( x \right )e^{-iE_nt/\hbar}=c_1\phi_1\left ( x \right )e^{-iE_1t/\hbar}+c_2\phi_2\left ( x \right )e^{-iE_2t/\hbar}$ does not describe a stationary state because:

$\left | \psi\left ( x,t \right ) \right |^{2}=c_{1}^{*}c_1\phi_{1}^{*}(x)\phi_{1}(x)+c_{2}^{*}c_2\phi_{2}^{*}(x)\phi_{2}(x)+c_{1}^{*}c_2\phi_{1}^{*}(x)\phi_{2}(x)e^{i(E_1-E_2)t/\hbar}+c_{2}^{*}c_1\phi_{2}^{*}(x)\phi_{1}(x)e^{i(E_2-E_1)t/\hbar}$

where the last two terms of the RHS of the last equality are time-dependent.

If $\phi_!$ and $\phi_2$ describe a degenerate state, where $E_1=E_2=E$ , then $\psi\left ( x,t \right )$ describes a stationary state. Since an observable of a stationary state, e.g. $H$ , is independent of time, every measurement of $H$ of systems in such a state results in the same value $E$ .

Next article: dirac bra-ket notation

Previous article: ground state

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

July 13, 2022September 26, 2024

Ground state (quantum mechanics)

The ground state of a system is the lowest energy state of the system.

The state of a system is dependent on the way electrons are distributed in a chemical species. A distribution that results in the system having the lowest energy is the ground state of the system. Every other distribution configuration is associated with a higher energy state known as an excited state. For example, the ground state of carbon is given by the term symbol ³P, while the term symbols ¹D and ¹S denote excited states of carbon.

Next article: stationary state

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

November 8, 2019August 3, 2025

1st order consecutive reaction

A 1st order consecutive reaction of the type A → B → C is composed of the reactions:

$A\rightarrow B\; \; \; \; \; \; \; v_1=k_1[A]$

$B\rightarrow C\; \; \; \; \; \; \; v_2=k_2[B]$

The rate laws are:

$\frac{d[A]}{dt}=-k_1[A]\; \; \; \; \; \; \; \; 20$

$\frac{d[B]}{dt}=k_1[A]-k_2[B]$

$\frac{d[C]}{dt}=k_2[B]$

To understand how a 1^st order consecutive reaction proceeds over time, we need to develop equations for $[A]$ , $[B]$ and $[C]$ . The expression for $[A]$ is the solution for eq20, i.e. $[A]=[A_0]e^{-k_1t}$ . Substituting this in the 2nd rate law above and rearranging gives:

$\frac{d[B]}{dt}+k_2[B]=k_1[A_0]e^{-k_1t}\; \; \; \; \; \; \; \; 21$

Eq21 is a linear first order differential equation of the form y’ + P(t)y = f(t). Multiplying eq21 with the integrating factor $e^{k_2t}$ , we have

$e^{k_2t}\frac{d[B]}{dt}+k_2e^{k_2t}[B]=k_1e^{k_2t}[A_0]e^{-k_1t}\; \; \; \; \; \; \; \; 22$

The LHS of eq22 is the derivative of the product of $e^{k_2t}$ and [B], i.e. $\frac{d\left ( e^{k_2t}[B] \right )}{dt}$ . So,

$\frac{d\left ( e^{k_2t}[B] \right )}{dt}=k_1e^{k_2t}[A_0]e^{-k_1t}$

Integrating both sides with respect to time, noting that [B] = 0 at t = 0, and rearranging, we have

$[B]=\frac{k_1}{k_2-k_1}\left ( e^{-k_1t}-e^{-k_2t} \right )[A_0]\; \; \; \; \; \; \; \; eq23$

As t → ∞, [B] = 0.

At all times, [A] + [B] + [C] = [A₀], so from eq23,

$[A_0]-[A]-[C]=\frac{k_1}{k_2-k_1}\left ( e^{-k_1t}-e^{-k_2t} \right )[A_0]$

Substituting $[A]=[A_0]e^{-k_1t}$ in the above equation and rearranging yields:

$[C]=\left( 1+\frac{k_1e^{-k_2t}-k_2e^{-k_1t}}{k_2-k_1} \right )[A_0]$

As t → ∞, [C] = [A₀].

NExt article: 2nd order reaction of the type (A+B→P)

Previous article: 1st order reversible reaction

Content page of advanced chemical kinetics

Content page of Advanced chemistry

Main content page

November 8, 2019May 9, 2025

1st order reversible reaction

A 1st order reversible reaction of the type $A\rightleftharpoons B$ is composed of the reactions:

$A\rightarrow B\; \; \; \; \; \; \; v_1=k_1[A]$

$B\rightarrow A\; \; \; \; \; \; \; v_2=k_2[B]$

The rate law is:

$\frac{d[A]}{dt}=-k_1[A]+k_2[B]$

Substituting [B] = [A₀] – [A], where [A₀] is the initial concentration of A, in the above equation and rearranging yields:

$\frac{d[A]}{dt}=-(k_1+k_2)[A]+k_2[A_0]\; \; \; \; \; \; \; \; 16$

Let

$x=(k_1+k_2)[A]-k_2[A_0]\; \; \; \; \; \; \; \; 17$

Eq16 becomes $\frac{d[A]}{dt}=-x$ . Differentiating eq17 with respect to [A], we have $d[A]=\frac{dx}{k_1+k_2}$ , and differentiating this expression with respect to time, we have $\frac{d[A]}{dt}=\frac{1}{k_1+k_2}\frac{dx}{dt}$ , which is equivalent to

$-x=\frac{1}{k_1+k_2}\frac{dx}{dt}\; \; \Rightarrow \; \; -(k_1+k_2)dt=\frac{dx}{x}$

Let x = x₀when t =0 and integrate the above expression. We have

$-(k_1+k_2)t=lnx-lnx_0\; \; \; \; \; \; \; \; 18$

Substituting eq17 in eq18, noting that the 2nd term on RHS of eq18 refers to concentrations at t = 0, where [A] = [A₀], gives

$-(k_1+k_2)t=ln\frac{(k_1+k_2)[A]-k_2[A_0]}{(k_1+k_2)[A_0]-k_2[A_0]}$

which rearranges to

$[A]=\frac{k_2+k_1e^{-(k_1+k_2)t}}{k_1+k_2}[A_0]\; \; \; \; \; \; \; \; 19$

When t = 0, eq19 becomes [A] = [A₀]. As t → ∞,

$[A_\infty ]=[A_{eqm}]=\frac{k_2}{k_1+k_2}[A_0]$

Since $[B_{eqm}]=[A_0]-[A_\infty ]$ ,

$[B_{eqm}]=[A_0]-\frac{k_2}{k_1+k_2}[A_0]=[A_0]\frac{k_1}{k_1+k_2}$

Therefore, the equilibrium constant for the reaction is:

$K=\frac{[B_{eqm}]}{[A_{eqm}]}=\frac{k_1}{k_2}$

This is the link between chemical kinetics and thermodynamics.

Next article: 1st order consecutive reaction

Previous article: Transition state theory

Content page of advanced chemical kinetics

Content page of Advanced chemistry

Main content page

November 8, 2019October 18, 2024

3rd order reaction of the type (A + B + C → P)

The rate law for the 3rd order reaction of the type A + B + C → P is:

$\frac{d[A]}{dt}=-[A][B][C]$

Using the same logic described in a previous article, we can rewrite the rate law as:

$\frac{dx}{dt}=k(a-x)(b-x)(c-x)$

where a = [A₀], b = [B₀] and c = [C₀].

Integrating the above equation throughout gives

$\int_{0}^{x}\frac{dx}{(a-x)(b-x)(c-x)}=k\int_{0}^{t}dt$

Substituting the partial fraction expression $\small \frac{1}{(a-x)(b-x)(c-x)}=\frac{1}{(a-x)(b-a)(c-a)}+\frac{1}{(b-x)(a-b)(c-b)}+\frac{1}{(c-x)(a-c)(b-c)}$ in the above integral and working out some algebra yields

$kt=\frac{1}{(b-a)(c-a)}ln\frac{a}{a-x}+\frac{1}{(a-b)(c-b)}ln\frac{b}{b-x}+\frac{1}{(a-c)(b-c)}ln\frac{c}{c-x}$

Next article: Maxwell-Boltzmann distribution

Previous article: 3rd order reaction of the type (A+2B→P)

Content page of advanced chemical kinetics

Content page of Advanced chemistry

Main content page

November 8, 2019October 18, 2024

3rd order reaction of the type (A + 2B → P)

The rate law for the 3rd order reaction of the type A + 2B → P is:

$\frac{d[A]}{dt}=-k[A][B]^2$

Using the same logic described in a previous article, we can rewrite the rate law as:

$\frac{dx}{dt}=k(a-x)(b-2x)^2$

where a = [A₀] and b = [B₀].

Integrating the above equation throughout yields

$\int_{0}^{x}\frac{dx}{(a-x)(b-2x)^2}=k\int_{o}^{t}dt\; \; \; \; \; \; \; \; 15$

Substituting the partial fraction expression $\frac{1}{(a-x)(b-2x)^2}=\frac{2}{(2a-b)(b-2x)^2}+\frac{1}{(2a-b)^2(a-x)}-\frac{2}{(2a-b)^2(b-2x)}$ in eq15 and working out some algebra gives

$kt=\frac{2x}{b(2a-b)(b-2x)}+\frac{1}{(2a-b)^2}ln\frac{a(b-2x)}{b(a-x)}$

Question

How to compute $\int_{0}^{x}\frac{2}{(2a-b)(b-2x)^2}dx$ ?

Answer

$\int_{0}^{x}\frac{2}{(2a-b)(b-2x)^2}dx=\int_{0}^{x}\frac{2b}{b(2a-b)(b-2x)^2}dx$

$=\int_{0}^{x}\frac{2[(b-2x)+2x]}{b(2a-b)(b-2x)^2}dx=\int_{0}^{x}\frac{2[(2a-b)(b-2x)+2x(2a-b)]}{b(2a-b)^2(b-2x)^2}dx$

$=\int_{0}^{x}\frac{2b(2a-b)(b-2x)-4bx(b-2a)}{b^2(2a-b)^2(b-2x)^2}dx=\frac{2x}{b(2a-b)(b-2x)}$

Note that the integrand in the 5th equality can be obtained by differentiating the last term using the quotient rule.

Next article: 3rd order reaction of the type (A+B+c→P)

Previous article: 2nd order autocatalytic reaction

Content page of advanced chemical kinetics

Content page of Advanced chemistry

Main content page

November 8, 2019October 16, 2024

2nd order autocatalytic reaction

An autocatalytic reaction is one in which a product catalyses the reaction. An example is the Mn²⁺-catalysed oxidation of oxalic acid by potassium manganate (VII):

$2MnO_4^{\; -}+16H^++5C_2O_4^{\; 2-}\rightarrow 2Mn^{2+}+10CO_2+8H_2O$

The equation can be reduced to A + P → 2P, or simply, A → P, with the rate law:

$\frac{d[A]}{dt}=-k[A][P]\; \; \; \; \; \; \; \; 13a$

Using the same logic described in a previous article, we can rewrite the rate law as:

$\frac{dx}{dt}=k(a-x)(p+x)$

where a = [A₀] and p = [P₀].

Integrating throughout, we have

$\int_{0}^{x}\frac{dx}{(a-x)(p+x)}=k\int_{0}^{t}dt\; \; \; \; \; \; \; \; 14$

Substituting the partial fraction expression $\frac{1}{(a-x)(p+x)}=\frac{1}{a+p}\left ( \frac{1}{a-x}+\frac{1}{p+x} \right )$ in eq14 and working out the algebra yields

$kt=\frac{1}{a+p}ln\frac{a(p+x)}{p(a-x)}$

which is equivalent to

$kt=\frac{1}{[A_0]+[P_0]}ln\frac{[A_0][P]}{[P_0][A]}$

Question

The mechanism of the above reaction is found to include the following steps:

$A+P\rightleftharpoons AP$

$AP\rightarrow P+P\; \; \; \; \; \; (rds)$

With this in mind, derive the rate law and show that it is consistent with eq13a.

Answer

We can write the rate law as:

$\frac{d[P]}{dt}=2k_{rds}[AP]=2k_{rds}K[A][P]=k[A][P]$

where K is the equilibrium constant for the 1st step and k = 2k_rdsK. Furthermore, the overall reaction is A → P, which means that

$\frac{d[P]}{dt}=-\frac{d[A]}{dt}=k[A][P]$

Next article: 3rd order reaction of the type (A+2B→P)

Previous article: 2nd order reaction of the type (A+2B→P)

Content page of advanced chemical kinetics

Content page of Advanced chemistry

Main content page

November 8, 2019September 26, 2024

2nd order reaction of the type (A + 2B → P)

The rate law for the 2nd order reaction of the type A + 2B → P is:

$\frac{d[A]}{dt}=-k[A][B]$

Using the same logic described in the previous article, we can rewrite the rate law as:

$\frac{dx}{dt}=k(a-x)(b-2x)$

where a = [A₀] and b = [B₀].

Rearranging the above equation and integrating throughout, we have

$\int_{0}^{x}\frac{dx}{(a-x)(\frac{b}{2}-x)}=2k\int_{0}^{t}dt\; \; \; \; \; \; \; \; 13$

Substituting the partial fraction expression $\frac{1}{(a-x)(\frac{b}{2}-x)}=\frac{1}{a-\frac{b}{2}}\left ( \frac{1}{\frac{b}{2}-x}-\frac{1}{a-x} \right )$ in eq13 and after some algebra, we have,

$kt=\frac{1}{b-2a}ln\frac{a(b-2x)}{b(a-x)}$

which is equivalent to

$kt=\frac{1}{[B_0]-2[A_0]}ln\frac{[A_o]([B])}{[B_0]([A])}$

Next article: 2nd order Autocatalytic reaction

Previous article: 2nd order reaction of the type (A+B→P)

Content page of advanced chemical kinetics

Content page of Advanced chemistry

Main content page

November 7, 2019September 20, 2025

Transition state theory

The transition state theory provides a theoretical way to calculate the pre-exponential factor A and the activation energy E_a, and therefore the rate constant k of an elementary chemical reaction. This is in contrast with the Arrhenius equation, where A and E_a are obtained empirically. The theory is based on statistical thermodynamics and can be illustrated for a gas-phase bimolecular reaction using the following assumptions:

1) The reacting system, expressed as $A+B\rightleftharpoons C^{\ddagger}\rightarrow P$ , proceeds along an energy path that includes a point of highest potential energy called the saddle point, where a distinct species known as the activated complex $C^{\ddagger}$ is formed. The conversion of the activated complex to the product P can be seen as an asymmetric vibrational stretch:

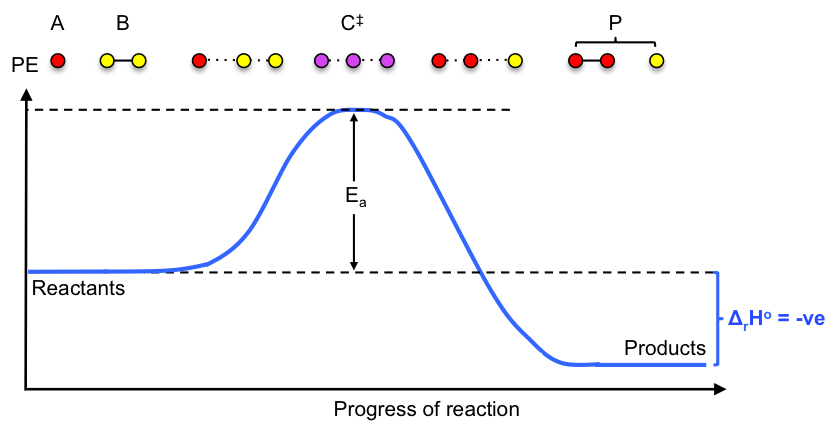
2) A rapid pre-equilibrium is established between the activated complex and the reactants: $A+B\rightleftharpoons C^{\ddagger}$ .

3) The rate of the reaction is attributed to the rate-determining step, which is the rate of conversion of the activated complex to the product: $rate=k^{\ddagger}[C^{\ddagger}]$ , where $k^{\ddagger}$ is proportional to the vibrational frequency $v$ of the activated complex.

The expression for the gas-phase rapid equilibrium from assumption 2 is:

$K^{\ddagger}=\frac{\frac{p_{c^{\ddagger}}}{p^o}}{\frac{p_A}{p^o}\frac{p_B}{p^o}}=\frac{p^op_{C^{\ddagger}}}{p_Ap_B}$

which in terms of molar concentration is:

$K^{\ddagger}=\frac{p^o}{RT}\frac{[C^{\ddagger}]}{[A][B]}\; \; \; \; \; \; \; \; 1$

Substituting eq1 into the rate equation , $rate=k^{\ddagger}[C^{\ddagger}]$ , yields:

$rate=k[A][B]\; \; \; \; \; \; \; where\; k=\frac{RT}{p^o}k^{\ddagger}K^{\ddagger}$

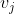In general, the equilibrium constant, when written in terms of standard molar partition functions, is $K=\left [ \prod _j\left ( \frac{q^o_{j,m}}{N_A} \right )^{v_j} \right ]e^{-\frac{\Delta_rE_0}{RT}}$ (see this article for derivation), where $v_j$ is the respective stoichiometric coefficient of the J-th species. For our bimolecular reaction,

$K^{\ddagger}=\frac{N_A\, q^o_{C^{\ddagger},m}}{q^o_{A,m}q^o_{B,m}}e^{-\frac{\Delta_rE_0}{RT}}\; \; \; \; \; \; \; \; 2$

where $\Delta_rE_0=E_0(C^{\ddagger})-E_0(A)-E_0(B)$ .

The activated complex in our example is a linear molecule with N = 3 atoms and therefore has 3N – 5 = 4 modes of vibration (2 bending, 1 symmetric stretch and 1 asymmetric stretch). The standard molar partition function for the activated complex is the product of the partition functions of different modes of motion: $q^o_{C^{\ddagger},m}=q^{o\; \; \; \; \; \; T}_{C^{\ddagger},m}q^{o\; \; \; \; \; \; V}_{C^{\ddagger},m}q^{o\; \; \; \; \; \; R}_{C^{\ddagger},m}$ , which we can rewrite in the form: $q^o_{C^{\ddagger},m}=q^{o\; \; \; \; \; V_{asym}}_{C^{\ddagger},m}\, \bar{q}^{\, o}_{C^{\ddagger},m}$ , where $\bar{q}^{\, o}_{C^{\ddagger},m} =q^{o\; \; \; \; \; T}_{C^{\ddagger},m}\, q^{o\; \; \; \; \; V_{others}}_{C^{\ddagger},m}\, q^{o\; \; \; \; \; R}_{C^{\ddagger},m}$ .

The standard molar partition function for the asymmetric vibration is $q^{o\; \; \; \; \; \; V_{asym}}_{C^{\ddagger},m}=\frac{1}{1-e^{-\frac{hv}{kT}}}$ , where $v$ is the vibrational frequency that leads to the conversion of the activated complex to the product. Assuming $\frac{hv}{kT}\ll 1$ , $q^{o\; \; \; \; \; \; V_{asym}}_{C^{\ddagger},m}=\frac{1}{1-e^{-\frac{hv}{kT}}}\approx\frac{kT}{hv}$ . Therefore,

$q^o_{C^{\ddagger},m}=q^{o\; \; \; \; \; V_{asym}}_{C^{\ddagger},m}\, \bar{q}^{\, o}_{C^{\ddagger},m}\approx\frac{kT}{hv}\bar{q}^{\, o}_{C^{\ddagger},m}\; \; \; \; \; \; \; \; 3$

Substituting eq3 into eq2 gives:

$K^{\ddagger}=\frac{kT}{hv}\bar{K}^{\ddagger}\; \; \; \; \; \; \; \; 4$

where $\bar{K}^{\ddagger}=\frac{N_A\, \bar{q}^{\, o}_{C^{\ddagger},m}}{q^o_{A,m}q^o_{B,m}}e^{-\frac{\Delta_rE_0}{RT}}$

Substituting eq4 into the rate constant equation $k=\frac{RT}{p^o}k^{\ddagger}K^{\ddagger}$ yields:

$k=\frac{RT}{p^o}k^{\ddagger}\frac{kT}{hv}\bar{K}^{\ddagger}\; \; \; \; \; \; \; \; 5$

From assumption 3, $k^{\ddagger}$ is proportional to the vibrational frequency $v$ of the activated complex,

$k^{\ddagger}=\kappa v\; \; \; \; \; \; \; \; 6$

where $\kappa$ is the proportionality constant called the transmission coefficient, which accounts for the notion that not every oscillation of the activated complex leads to its conversion to the product.

Substituting eq6 into eq5 results in:

$k=\kappa\frac{RT}{p^o}\frac{kT}{h}\bar{K}^{\ddagger}\; \; \; \; \; \; \; \; 7$

The standard Gibbs energy is $\Delta G^o=-RTlnK$ . By analogy, we define the standard Gibbs activation energy as $\Delta^{\ddagger}G^o=-RTln\bar{K}^{\ddagger}$ , which we shall substitute into eq7 to give:

$k=\kappa\frac{RT}{p^o}\frac{kT}{h}e^{-\frac{\Delta^{\ddagger}G^o}{RT}}=\kappa\frac{RT}{p^o}\frac{kT}{h}e^{\frac{\Delta^{\ddagger}S^o}{R}}e^{-\frac{\Delta^{\ddagger}H^o}{RT}}\; \; \; \; \; \; \; \; 8$

Question

Is the expression for standard Gibbs activation energy still valid when the equilibrium constant now excludes the factor $q_{C^{\ddag},m}^{o}\, ^{V_{asym}}$ ?

Answer

It is an approximation that we make, which delivers an expression for the rate constant that is in good agreement with experimental values.

Eq7 and eq8 are different forms of the Eyring equation. Substituting eq8 in the definition of activation energy $E_a=RT^2\frac{\partial lnk}{\partial T}$ and differentiating, noting that $\Delta^{\ddagger}S^o$ and $\Delta^{\ddagger}H^o$ are standard states, which are temperature-independent, gives:

$E_a=\Delta^{\ddagger}H^o+2RT\; \; \; \; \; \; \; \; \; 9$

Substituting eq9 into eq8 yields:

$k=\kappa e^2\frac{RT}{p^o}\frac{kT}{h}e^\frac{\Delta^{\ddagger}S^o}{R}e^{-\frac{E_a}{RT}}\; \; \; \; \; \; \; \; 10$

Comparing eq10 and the Arrhenius equation, we have:

$A=\kappa e^2\frac{RT}{p^o}\frac{kT}{h}e^\frac{\Delta^{\ddagger}S^o}{R}$

Repeating all the above steps for a gas-phase unimolecular reaction, we arrive at an activation energy of $E_a=\Delta^{\ddagger}H^o+RT$ instead of eq9. Therefore, the transition state theory predicts that the activation energy for a gas-phase elementary reaction is

$E_a=\Delta^{\ddagger}H^o+xRT$

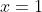where $x=1$ for a unimolecular reaction and 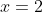$x=2$ for a bimolecular reaction.

Next article: 1st order reversible reaction

Content page of advanced chemical kinetics

Content page of Advanced chemistry

Main content page

November 7, 2019October 16, 2024

2nd order reaction of the type (A + B → P)

The rate law for the reaction A + B → P is:

$\frac{d[A]}{dt}=-k[A][B]\; \; \; \; \; \; \; \; 11$

Unlike the 2nd order reaction of the type A → P with a rate law of $\frac{d[A]}{dt}=-k[A]^2$ , eq11 cannot be integrated unless we express [B] in terms of [A], or [A] and [B] in terms of a third variable x. Since A and B react in a ratio of 1:1, the remaining concentrations of A and B at any time of the reaction are: