Centrifugal distortion

Centrifugal distortion refers to the deformation of a molecule’s structure that occurs due to the rotational motion of the molecule.

As a molecule rotates, the centrifugal force, which acts outward from the axis of rotation, causes the molecule’s bond lengths and bond angles to stretch and distort, particularly at higher rotational speeds. This effect is most pronounced in larger, heavier molecules, where the rotational energy is sufficient to cause a noticeable shift in the geometry. Centrifugal distortion is an important factor in molecular spectroscopy, as it can influence the rotational energy levels of a molecule, leading to shifts in the observed spectral lines, and must be accounted for when interpreting high-resolution rotational spectra.

What is centrifugal force, and how is it different from centripetal force?

Centripetal force and centrifugal force are both associated with circular motion, but they are described in different frames of reference. Centripetal force is described in an inertial frame of reference or in a frame where the object is experiencing actual physical forces that are measurable and observable. In the inertial frame, the force that keeps the object in circular motion is real and necessary to counteract the object’s tendency to move in a straight line (due to inertia).

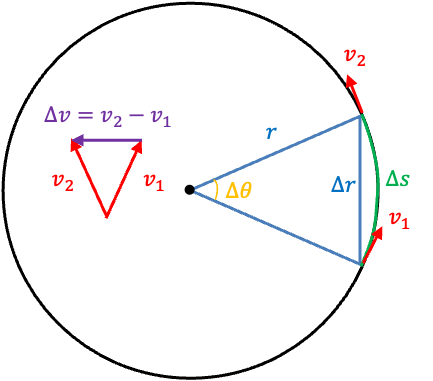
Consider a particle moving around a circle (see diagram above) of radius $r$ with an instantaneous velocity $v_1$ at $t=t$ and $v_2$ at $t=t'$ , where $\vert v_1\vert=\vert v_2\vert=v$ . If $\Delta\theta$ is small, the arc length $\Delta s$ is approximately equal to $\Delta r$ and hence to $\Delta v$ . Since the ratio of corresponding sides of two similar triangles is always equal, $\frac{\Delta v}{v}=\frac{\Delta s}{r}$ . Dividing both sides of this equation by $\Delta t$ and rearranging (noting that $a=\frac{\Delta v}{\Delta t}$ and $v=\frac{\Delta s}{\Delta t}$ ) gives:

$a=\frac{v^2}{r}\;\;\;\;\;\;\;\;85$

Substituting $v=r\omega$ (see this article for details) into eq85 yields:

$a=r\omega^2\;\;\;\;\;\;\;\;86$

Therefore the centripetal force $F$ acting on the rotating particle of reduced mass $\mu$ is

$F=\mu r\omega^2\;\;\;\;\;\;\;\;87$

Centrifugal force, on the other hand, is experienced in a non-inertia frame of reference (rotating frame). It appears to act outward on the rotating particle. However, it does not correspond to any real physical force but is instead a fictitious force introduced to account for the observed effects of acceleration in the rotating frame. Since the magnitude of centrifugal force is the same as that of the centripetal force, the magnitude of the centrifugal force experienced by a diatomic molecule of reduced mass $\mu$ and bond length $r$ rotating at angular velocity $\omega$ is $\mu r\omega^2$ .

Question

Explain how the fictitious centrifugal force accounts for the observed effects of acceleration in the rotating frame?

Answer

Consider a ball tied to a string, rotating in a horizontal plane. In the inertia frame of reference, the only force acting on the ball is the centripetal force, directed towards the axis of rotation. In the rotating frame of reference, the centripetal force still acts on the ball, even though the ball appears stationary. This would imply that the ball should accelerate towards the centre, contradicting the observation that it remains at rest in the rotating frame. Therefore, a fictitious force, equal in magnitude to the centripetal force but acting in the opposite direction, must be introduced to restore consistency with Newton’s second law.

At equilibrium, the centrifugal force (or the centripetal force) equals the restoring force given by Hooke’s law:

$\mu r\omega^2=k(r-r_0)\;\;\;\;\;\;\;\;88$

where $k$ is the force constant and $r_0$ is the equilibrium bond length.

For small displacements, the motion expressed by eq88 is simple harmonic, with the following classical Hamiltonian for the system:

$H=\frac{J^2}{2\mu r^2}+\frac{1}{2}k(r-r_0)^2\;\;\;\;\;\;\;\;89$

where the kinetic energy term is given by the classical form of eq4a and the potential energy term is derived from this article.

Rearranging eq88 results in $r=\frac{1}{1-\mu\omega^2/k}r_0$ , and therefore

$\frac{1}{r^2}=\frac{1}{r_0^2}-\frac{2\mu\omega^2}{kr^2_0}+\frac{\mu^2\omega^4}{k^2r^2_0}\;\;\;\;\;\;\;\;90$

For small displacements, $r\approx r_0$ , which implies from $r=\frac{1}{1-\mu\omega^2/k}r_0$ that $1-\frac{\mu\omega^2}{k}\approx 1$ , and hence $\vert\frac{\mu\omega^2}{k}\vert\ll 1$ . So, we can ignore the last term in eq90 as a first approximation, giving:

$\frac{1}{r^2}=\frac{1}{r_0^2}-\frac{2\mu\omega^2}{kr^2_0}\;\;\;\;\;\;\;\;91$

Substituting $J=I\omega=\mu r^2\omega$ (see this article for details) into RHS of eq91 gives:

$\frac{1}{r^2}=\frac{1}{r_0^2}-\frac{2J^2}{k\mu r^4r^2_0}\;\;\;\;\;\;\;\;92$

Substituting eq92 and eq88 into eq89 yields:

$H=\frac{J^2}{2\mu r_0^2}-\frac{J^4}{k\mu^2r^4r_0^2}+\frac{J^4}{2k\mu^2 r^6}\;\;\;\;\;\;\;\;93$

Since $r\approx r_0$ for small displacements, eq93 becomes:

$H=\frac{J^2}{2\mu r_0^2}-\frac{J^4}{2k\mu^2r_0^6}$

Using the quantum mechanics postulate that “to every observable quantity in classical mechanics there corresponds a linear, Hermitian operator in quantum mechanics”, and replacing the classical angular momentum $J$ with the quantum mechanical operator gives

$\hat{H}=\frac{\hat{J}^2}{2\mu r_0^2}-\frac{\hat{J}^4}{2k\mu^2r_0^6}\;\;\;\;\;\;\;\;94$

The corresponding eigenvalues of eq94 (derived using orbital angular momentum ladder operators) are:

$E=\frac{J(J+1)\hbar^2}{2\mu r_0^2}-\frac{J^2(J+1)^2\hbar^4}{2k\mu^2r_0^6}$

$E=hcBJ(J+1)-hcDJ^2(J+1)^2\;\;\;\;\;\;\;\;95$

where $B=\frac{\hbar}{4\pi c\mu r_0^2}$ is the rotational constant and $D=\frac{\hbar^3}{4\pi ck\mu^2r_0^6}$ is the centrifugal distortion constant.

However, rotational energies are typically reported as wavenumbers in molecular spectroscopy. Substituting $E=h\nu$ and $c=\nu\lambda$ into eq95 yields $\tilde{\nu}=BJ(J+1)-DJ^2(J+1)^2$ , which is a function of $J$ . Therefore,

$F(J)=BJ(J+1)-DJ^2(J+1)^2\;\;\;\;\;\;\;\;96$

Question

Can centrifugal distortion be observed from an inertia frame?

Answer

Yes, centrifugal distortion can indeed be observed from an inertial frame, though it’s important to clarify that there are no “fictitious forces” like centrifugal force in an inertial frame. However, centrifugal distortion is not a fictitious effect. It is a real, physical phenomenon that arises due to the rotation of the molecule, and this can be observed in an inertial reference frame.

In a non-rotating molecule, the bonds between atoms are at their equilibrium lengths, representing the most stable configuration where the bond is neither stretched nor compressed. When the molecule begins to rotate, each atom wants to move in a straight line (due to its inertia) tangentially away from the center of rotation. To keep the atoms moving in a circular path, the chemical bond must provide an inward pulling force (the centripetal force).

Just like a spring, a chemical bond can only exert a restoring force when it is displaced from its equilibrium position. To generate a small centripetal force (restoring force) during low-speed rotation, the bond needs to stretch only a little. For faster rotation, the bond must stretch more to provide a larger centripetal force. This stretching of the bond beyond its equilibrium length is the physical phenomenon of centrifugal distortion, which can be observed and measured in an inertia frame.

Centrifugal distortion

Question

Answer

Question

Answer

Previous article: Microwave spectra

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply