A pair of commuting operators that are Hermitian can have a common complete set of eigenfunctions.
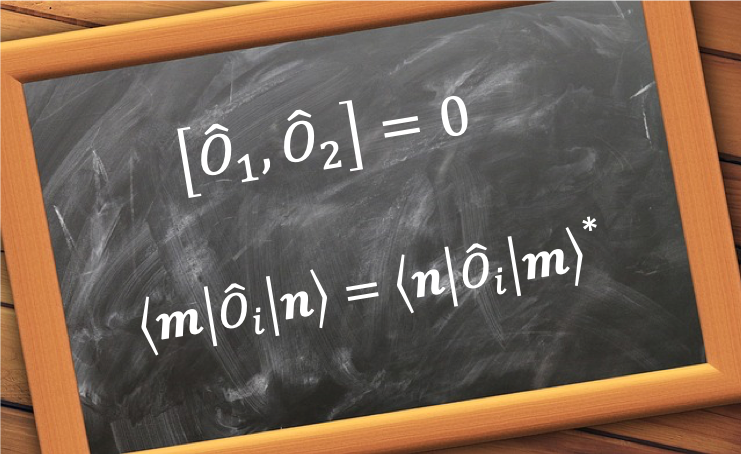
Let and
be two different operators, with observables
and
respectively.
So, . If this is so, we say that the two operators commute. The short notation for
is
, where in the case of two commuting operators,
.
When the effect of two operators depends on their order, we say that they do not commute, i.e. . If this is the case, we say that the observables
and
are complementary.
One important concept in quantum mechanics is that we can select a common complete set of eigenfunctions for a pair of commuting Hermitian operators. The proof is as follows:
Let and
be the complete sets of eigenfunctions of
and
respectively, such that
and
. If the two operators have a common complete set of eigenfunctions, we can express
as a linear combination of
:
For example, the eigenfunction is:
Since some of the eigenfunctions may describe degenerate states (i.e. some
are associated with the same eigenvalue
), we can rewrite
as:
where and
represents distinct eigenvalues of the complete set of eigenfunctions of
.
For example, if the linear combination of in eq6 has
and
describing the same eigenstate with eigenvalue
, and
and
describing another common eigenstate with eigenvalue
,
where ,
,
and so on.
In other words, eq7 is a sum of eigenfunctions with distinct eigenvalues of . Since a linear combination of eigenfunctions describing a degenerate eigenstate is an eigenfunction of
, we have
i.e. is an eigenfunction of
. Furthermore, the set
is complete, which is deduced from eq7, where the set
is complete.
From , we have:
Substituting eq7 in the above equation, we have
By operating on the 1st term of the summation in the above equation with , and using the fact that
commute with
,
Substituting eq8, where in the above equation,
Repeating the operation of on the remaining terms of the summation in eq9, we obtain equations similar to eq11 and we can write:
i.e. is an eigenfunction of
with distinct eigenvalues
. Since
is Hermitian and
are associated with distinct eigenvalues, the eigenfunctions
are orthogonal and therefore linearly independent. Consequently, each term in the summation in eq9 must be equal to zero:
This implies that , which is a complete set as mentioned earlier, is also an eigenfunction of
. Therefore, we can select a common complete set of eigenfunctions
for a pair of commuting Hermitian operators. Conversely, if two Hermitian operators do not commute, eq10 is no longer valid and we cannot select a common complete set of eigenfunctions for them.