A continuity equation in fluid mechanics is an equation that makes use of the conservation-of-mass theory to describe the transport of fluid.
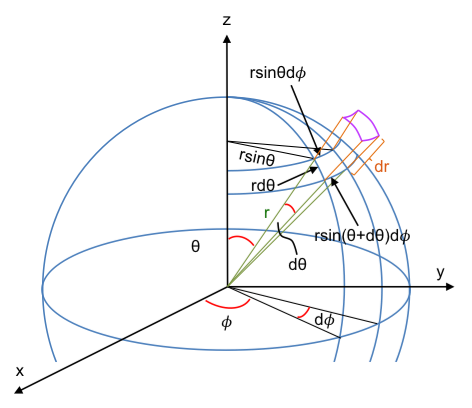
With reference to the above diagram, a control volume in spherical coordinates is given by:
where
r is the radius of the sphere
θ is the polar angle
Φ is the azimuthal angle
Substitute the formula for density V = m/ρ in eq1 and divide throughout by ∂t,
The flow velocity of the fluid is:
The net flow of fluid through the surfaces of the control volume in the radial direction can be expressed as the rate of change of mass through the surfaces in the radial direction:
Aout,r is the outflow area of the control volume in the radial direction, given by:
Substituting sin(θ+dθ) ≈ sinθ + cosθdθ (from the Maclaurin series of cosθ and sinθ for small θ) in eq5 and eliminating higher order terms (i.e. terms with dr2, dθ2):
Similarly, the inflow area of the control volume in the radial direction Ain,r is:
Substituting eq6 and eq7 in eq4 and eliminating higher order terms,
Repeating the above steps for the net flow of fluid through the surfaces of the control volume in the polar and azimuthal directions, we have:
Assuming steady fluid flow and the conservation of fluid mass, the fluxes of mass into the control volume must be equal to the fluxes of mass out of the control volume and the accumulation of mass in the control volume:
Substituting eq8, eq9 and eq10 in eq11, we have the continuity equation in spherical coordinates.
where
NExt article: Stokes stream function
Previous article: Overview
Content page of Stokes’ law
Content page of advanced chemistry
Main content page
