The equilibrium constant in statistical thermodynamics relates to the ratio of molecular partition functions for products and reactants. It reflects how molecular energy levels and their populations determine macroscopic equilibrium.
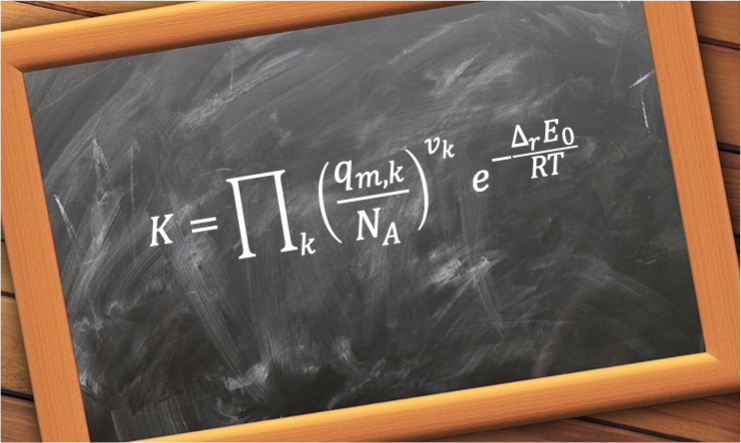
Consider the reaction
where is the stoichiometric coefficient of the species
in the reversible reaction. Note that the stoichiometric coefficients for reactants are negative by convention, while those for products are positive.
The reaction Gibbs energy for the reaction is:
Substituting eq329 into eq380 gives,
where the reaction zero-point energy change is .
Eq381 can be rewritten as:
Substituting eq8 into eq382 and rearranging yields:

Question
Show that eq383 is consistent with the classical thermodyamic equilibrium constant .
Answer
As is derived using
(see this article), we need to show that the statistical thermodynamics expression for the chemical potential of an ideal gas can be transformed into
. Substituting eq257 into eq330 yields:
Substituting eq266 into eq384 gives:
where .
Substituting the ideal gas law into eq385 gives:
or equivalently,
From eq386, we can define the standard chemical potential as . Then,
where is the activity of an ideal gas.