The Gibbs paradox refers to the apparent contradiction between statistical and classical thermodynamics where the entropy change for mixing identical gases is nonzero unless quantum indistinguishability is considered.
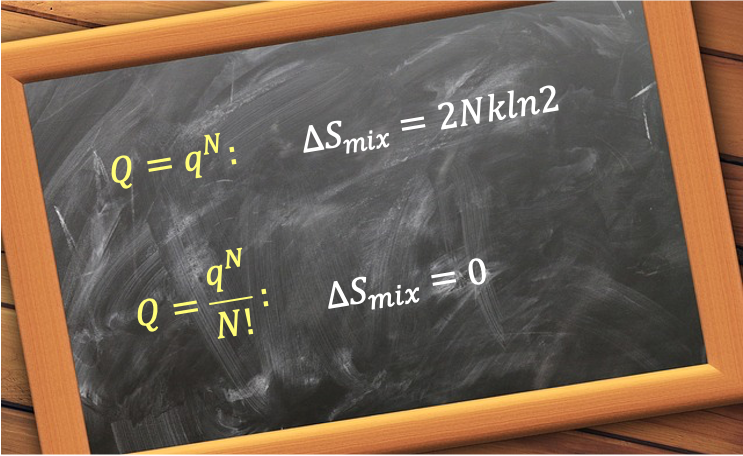
In classical thermodynamics, the entropy of mixing two gases should be zero if the gases are identical (nothing changes), and positive if the gases are different (mixing different gases leads to a greater number of possible microstates). To analyse whether statistical thermodynamics aligns with this, let’s consider a system of single-species, non-interacting, distinguishable particles. The canonical partition function is given by eq166:
where
is the molecular partition function
is the number of particles
Substituting eq166 into eq159 gives:
If the partition between two containers, each with identical gas particles occupying a volume
, is removed, the entropy of mixing
is:

Question
Show that .
Answer
From eq257, we have . The translational part of the molecular partition function
of the gas is proportional to
(see eq266), while the remaining components (rotational, vibrational and electronic) are independent of
. So,
In other words, is independent of
, and so,
.
Therefore,
Eq341 suggests an increase in entropy simply from removing a partition between two identical gases, even though nothing physical has changed (the final state is macroscopically the same as the initial one). This is not possible and leads to the Gibbs paradox.
To resolve the paradox, the partition function must be divided by . Substituting eq167 into eq159 gives:
So,
Using Stirling’s approximation, . Therefore, the entropy of mixing of two identical gases is zero only if the partition function correctly accounts for indistinguishability by dividing by
.