Koopmans’ theorem

Koopmans’ theorem states that the energy to remove an electron from an orbital of an atom, whose state is described by a single Slater determinant, is approximately the negative value of the corresponding Hartree-Fock orbital energy. In other words, the theorem states that the negative value of the orbital energy $E_k$ of an atom is approximately equal to the ionisation energy IE for the k-th electron in the atom.

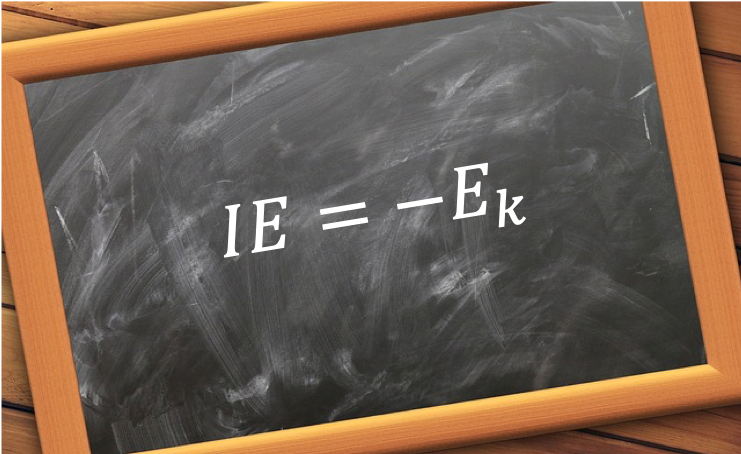
To prove the theorem, we begin with the ionisation process, which is generally expressed as

$X(g)+h\nu\rightarrow X^+(g)+e^-$

where $X$ is an atom, which is irradiated with a photon of energy $h\nu$ , and $X^+$ is the corresponding ion with an electron $e^-$ removed.

In terms of energies,

$h\nu=E_{X^+}-E_X+E_{e^-}$

where $E_{X^+}$ is the state of the ion, $E_X$ is the state of the atom and $E_{e^-}$ is the kinetic energy of the expelled electron.

As $E_{e^-}\rightarrow 0$ ,

$h\nu=IE=E_{X^+}-E_X\;\;\;\;\;\;\;\;(143)$

Substituting eq95 in eq143 gives

$IE=\sum_{i\neq k}^nH_i+\frac{1}{2}\sum_{j,i\neq k}^n(J_{ij}-K_{ij})-\sum_{i=1}^nH_i-\frac{1}{2}\sum_{j,i=1}^n(J_{ij}-K_{ij})$

$IE=-H_k+\frac{1}{2}\left[\sum_{j,i\neq k}^n(J_{ij}-K_{ij})-\sum_{j,i=1}^n(J_{ij}-K_{ij})\right]\;\;\;\;\;\;\;\;(144)$

Question

Show that $\sum_{j,i\neq k}^n(J_{ij}-K_{ij})-\sum_{j,i=1}^n(J_{ij}-K_{ij})=-2\sum_{j=1}^n(J_{kj}-K_{kj})$ .

Answer

Let $C=\sum_{j,i\neq k}^n(J_{ij}-K_{ij})-\sum_{j,i=1}^n(J_{ij}-K_{ij})$ . Expanding the equation and eliminating common terms,

$C=-\left[\sum_{i=1}^n(J_{ik}-K_{ik})+\sum_{j\neq k}^n(J_{kj}-K_{kj})\right]$

Since $J_{kk}-K_{kk}=0$ , we can add it to $\sum_{j\neq k}^n(J_{kj}-K_{kj})$ , giving

$C=-\left[\sum_{i=1}^n(J_{ik}-K_{ik})+\sum_{j=1}^n(J_{kj}-K_{kj})\right]$

Furthermore, $J_{ik}=J_{ki}$ and $K_{ik}=K_{ki}$ . So,

$C=-\left[\sum_{i=1}^n(J_{ki}-K_{ki})+\sum_{j=1}^n(J_{kj}-K_{kj})\right]$

Relabelling i to j for $\sum_{i=1}^n(J_{ki}-K_{ki})$

$C=-2\sum_{j=1}^n(J_{kj}-K_{kj})\;\;\;\;\;\;\;\;(145)$

Substituting eq145 in eq144 yields

$IE=-\left[H_k+\sum_{j=1}^n(J_{kj}-K_{kj})\right]\;\;\;\;\;\;\;\;(146)$

Relabelling t with j and $\lambda_r^{'}$ with $E_r$ in eq109, we have

$\left[\left(-\frac{1}{2}\nabla^2-\frac{Z}{r}\right)+\sum_{j\neq r}\int\phi_j^{'*}(x') \frac{(1-P_{rj})\phi_j^{'}(x')}{\vert\boldsymbol{\mathit{ r}}-\boldsymbol{\mathit{ r}}'\vert}dx'\right]\phi_r^{'}(x)=E_r\phi_r^{'}(x)\;\;\;\;(147)$

Multiplying the k-th equation in eq147 by $\phi_k^{'*}(x)$ and integrating over $dx$ , we have

$E_k=H_k+\sum_{j\neq k}^n(J_{kj}-K_{kj})$

Since $J_{kk}-K_{kk}=0$

$E_k=H_k+\sum_{j=1}^n(J_{kj}-K_{kj})\;\;\;\;\;\;\;\;(148)$

Substituting eq148 in eq146 results in

$IE=-E_k\;\;\;\;\;\;\;\;(149)$

Eq149 is known as Koopmans’ theorem.

Lastly, let’s study the relation between the relation between the orbital energy $E_k$ of an atom and the total energy E of the atom. From eq148,

$\sum_{k=1}^nE_k=\sum_{k=1}^nH_k+\sum_{k,j=1}^n(J_{kj}-K_{kj})$

$\sum_{k=1}^nE_k=\sum_{k=1}^nH_k+\sum_{j\neq k}\sum_{k=1}^n(J_{kj}-K_{kj})$

Substituting eq94 in the above equation gives

$E=\sum_{k=1}^nE_k-\frac{1}{2}\sum_{j\neq k}\sum_{k=1}^n(J_{kj}-K_{kj})\;\;\;\;\;\;\;\;(150)$

Question

Show that the alternative to eq150 is $E=\frac{1}{2}\sum_{k=1}^n(E_k+H_k)$ .

Answer

Adding $H_k$ to both sides of eq148 and summing throughout from $k=1,\cdots,n$ ,

$\sum_{k=1}^n(E_k+H_k)=2\sum_{k=1}^nH_k+\sum_{k,j=1}^n(J_{kj}-K_{kj})$ $=2\sum_{k=1}^nH_k+\sum_{j\neq k}\sum_{k=1}^n(J_{kj}-K_{kj})=2\left[\sum_{k=1}^nH_k+\sum_{k >j}\sum_{j=1}^n(J_{kj}-K_{kj})\right]$