Leibniz’s theorem extends the product rule to determine higher-order derivatives of the product of two or more functions.
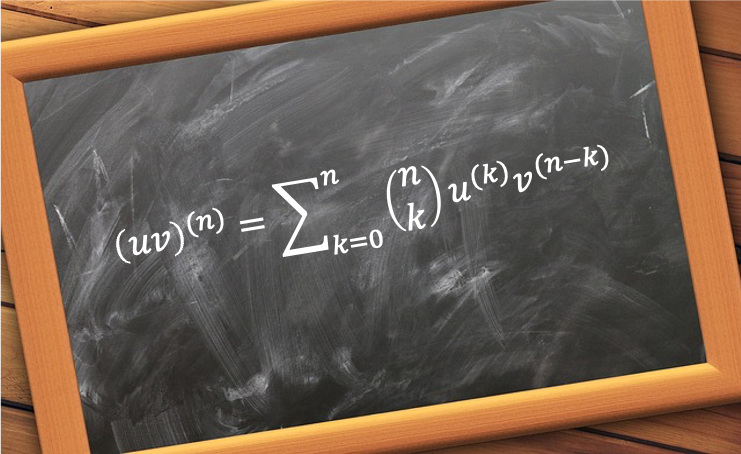
Consider the function =u(x)v(x))
, where 
and 
are 
times differentiable. Using the product rule, the first few derivatives are:
'=uv'+u'v)
''=uv''+2u'v'+u''v)
^{(3)}=uv^{(3)}+3u'v''+3u''v'+u^{(3)}v)
which suggests that the -th order derivative of 
can be expressed as the binomial expansion
^{(n)}=\sum_{k=0}^n\begin{pmatrix}n\\k\end{pmatrix}u^{(k)}v^{(n-k)}\;\;\;\;\;\;\;\;319a)
where and 
are non-negative integers, })
and })
are the 
-th order derivatives of and , respectively, and !})
are the binomial coefficients.
Eq319a is known as Leibniz’s theorem, which can be proven by induction. For 
,
^{(1)}=\begin{pmatrix}1\\0\end{pmatrix}u^{(0)}v^{(1)}+\begin{pmatrix}1\\1\end{pmatrix}u^{(1)}v^{(0)}=uv'+u'v)
If eq319a holds for all when 
, then for 
,
^{m+1}&=\frac{d}{dx}\sum_{k=0}^m\begin{pmatrix}m\\k\end{pmatrix}u^{(k)}v^{(m-k)}\\&=\sum_{k=0}^m\begin{pmatrix}m\\k\end{pmatrix}u^{(k+1)}v^{(m-k)}+\sum_{k=0}^m\begin{pmatrix}m\\k\end{pmatrix}u^{(k)}v^{(m-k+1)}\\&=\sum_{k=1}^{m+1}\begin{pmatrix}m\\k-1\end{pmatrix}u^{(k)}v^{(m-k+1)}+\sum_{k=0}^{m}\begin{pmatrix}m\\k\end{pmatrix}u^{(k)}v^{(m-k+1)}\\&=\sum_{k=1}^{m}\begin{pmatrix}m\\k-1\end{pmatrix}u^{(k)}v^{(m-k+1)}+\begin{pmatrix}m\\m\end{pmatrix}u^{(m+1)}v^{(0)}+\begin{pmatrix}m\\0\end{pmatrix}u^{(0)}v^{(m+1)}+\sum_{k=1}^{m}\begin{pmatrix}m\\k\end{pmatrix}u^{(k)}v^{(m-k+1)}\\&=\begin{pmatrix}m+1\\0\end{pmatrix}u^{(0)}v^{(m+1)}+\sum_{k=1}^{m}\biggr\[\begin{pmatrix}m\\k-1\end{pmatrix}+\begin{pmatrix}m\\k\end{pmatrix}\biggr\]u^{(k)}v^{(m-k+1)}+\begin{pmatrix}m+1\\m+1\end{pmatrix}u^{(m+1)}v^{(0)}\end{align})
Since 
(see this article for proof),
^{m+1}&=\begin{pmatrix}m+1\\0\end{pmatrix}u^{(0)}v^{(m+1)}+\sum_{k=1}^{m}\begin{pmatrix}m+1\\k\end{pmatrix}u^{(k)}v^{(m-k+1)}+\begin{pmatrix}m+1\\m+1\end{pmatrix}u^{(m+1)}v^{(0)}\\&=\sum_{k=0}^{m+1}\begin{pmatrix}m+1\\k\end{pmatrix}u^{(k)}v^{(m-k+1)}\end{align})
and the theorem holds for all and .