The mean molecular energy of a system of non-interacting molecules is defined as the average internal energy per molecule, calculated over all possible quantum states accessible to the molecule at a given temperature.
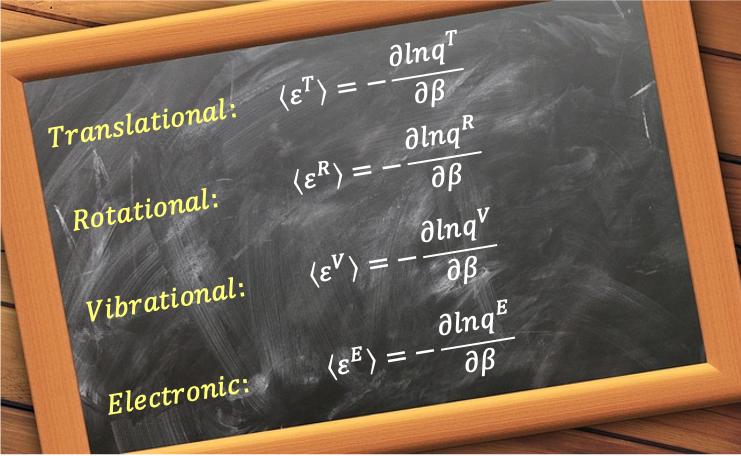
This average is weighted by the Boltzmann probability of each state and reflects the contributions from translational, rotational, vibrational and electronic motions, depending on the system’s complexity.
Mathematically, the mean molecular energy of a molecule in thermal equilibrium is given by:
where is energy the
-th state measured relative to the ground state energy of the molecule, and
is the probability of the molecule being in that state.
Substituting eq251 into eq300 gives:
where
is the molecular partition function,
is the Boltzmann constant,
is the absolute temperature,
.
Since and
, eq301 can be expressed as:
or

Question
Why does eq303 (or eq302) involve a partial derivative?
Answer
A partial derivative is used because may be dependent on a few variables, such as
and
(see eq266).
Substituting eq257 into eq303 yields:
where ,
,
and
.
Mean translational energy
The mean translational energy of a non-interacting molecule is derived by substituting eq266 into
to give:

Question
Show that each of the three components of is equal to
.
Answer
Substituting eq261 into results in:
Let’s focus on the first derivative in eq306. Substituting eq265 into it yields:
Similarly, each of the other two components is equal to because
and
.
Thus, each translational degree of freedom contributes , consistent with the equipartition theorem.
Mean rotational energy
The mean rotational energy of a non-interacting heteronuclear linear molecule at low temperatures is derived by substituting eq270 into
to give:
At very low temperatures, almost all molecules occupy the ground state with , so eq307 reduces to
. As the temperature increases,
is approximately given by expanding the summations in eq307 and differentiating to yield:
At higher temperatures, we substitute eq275, where and
, into
to give:
which is consistent with the equipartition theorem.
Since the symmetry number cancels out, the mean rotational energy of a non-interacting symmetrical linear molecule at high temperatures is also
. Unlike linear rotors, which have two independent rotational degrees of freedom, spherical rotors, symmetric rotors and asymmetric rotors have three. Substituting eq280, eq286 and eq287 separately into
and differentiating results in
for each of the three types of rotors, which is again consistent with the equipartition theorem.
Mean vibrational energy
The mean vibrational energy of a non-interacting diatomic molecule oscillating harmonically at low temperatures is derived by substituting eq291 into
, where
, to give:
If we compute the derivative in eq310 and multiply the result by , we get:
At high temperatures, , which allows us to expand
as a Taylor series (
) to give:
As mentioned in an earlier article, eq291 evaluates absolute energy levels, including the zero-point energy. If we derive using eq293 instead of eq291, we obtain:
Although the equipartition theorem states that the mean vibrational energy of a classical oscillator at high temperatures is equal to , both eq312 and eq313 are consistent with this result. This is because the theorem accounts only for the thermal contribution to vibrational energy; the zero-point energy term
is a quantum mechanical artifact that is independent of temperature.
For polyatomic molecules, each normal mode of vibration behaves approximately like a separate harmonic oscillator, with the total vibrational partition function given by eq294:
where for non-linear molecules,
for linear molecules, and
is the number of atoms.
So,
Since ,
In other words, the total mean vibrational energy of a non-interacting polyatomic molecule oscillating harmonically is the sum of the mean energy of each normal mode. This implies that
which are consistent with the equipartition theorem at high temperatures.
Mean electronic energy
The mean electronic energy of a non-interacting molecule is derived by substituting eq296, where
, into
to give:
At low temperatures, . Therefore, all the numerator terms in eq315 approach zero, giving:
This can be explained qualitatively: the energy gap between the ground electronic state and the first excited electronic state of a typical molecule is very large, which results in the molecule occupying only the electronic ground state, which has zero energy.
At higher temperatures, the mean electronic energy increases as excited electronic states become thermally accessible. However, this regime is often not reached before the molecule dissociates