The molecular partition function is a mathematical expression that describes how a non-interacting particle in a system is distributed among different energy levels at a given temperature.
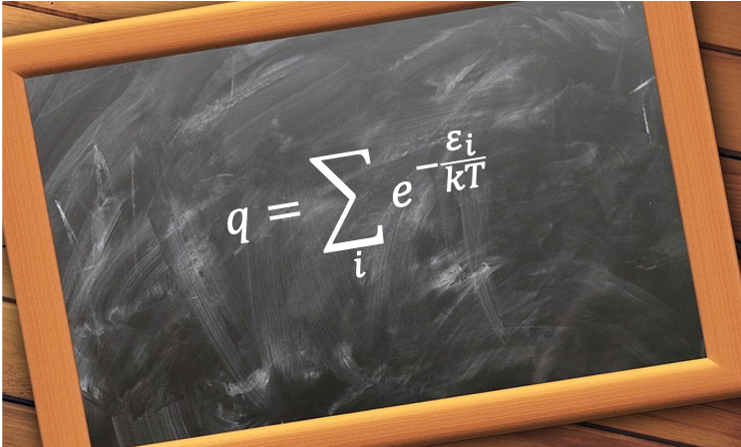
It naturally emerges when analysing the canonical partition function of a system composed of non-interacting, distinguishable particles. Under these conditions, the total partition function factorises into a product of single-particle partition functions, allowing the definition of the molecular partition function as the canonical partition function of an individual particle.
Mathematically, it is given by
where is the
-th energy level of the particle and
is the Boltzmann constant.
It is also equivalent to the denominator of the Boltzmann distribution, which gives the probability of finding a particle in the
-th energy state at thermal equilibrium:

Question
What are non-interacting molecules?
Answer
Non-interacting molecules behave independently and do not interact with one another through forces such as chemical bonding, electrostatic attraction/repulsion or van der Waals forces. The energy levels of each molecule are determined solely by its own internal structure (electronic, vibrational, rotational and translational states), and not altered by the presence of nearby molecules. Ideal gases, or very dilute gases where interactions are negligible, can be considered systems containing non-interacting molecules.
We know that is a function of temperature
, but why is it called a partition function? Consider the case when
is very high. In this limit, each term in the sum approaches 1. Conversely, when
, only the term with
(the ground state) is equal to 1. This means that
tells us how many energy states are accessible to a molecule at a given temperature. When it appears in the Boltzmann distribution, it then reveals how the total probability is partitioned among the available energy levels.
Although the molecular partition function is defined for a single molecule, it can be used to describe the behaviour of a collection of non-interacting molecules in a system. This is because, when the molecules do not interact, the probability that any one molecule occupies a particular energy state given by eq50, also represents the fraction of all molecules found in that state at thermal equilibrium. This situation is analogous to rolling a four-sided biased die, where each face has a different probability of appearing. In this analogy, the probability of a particular outcome corresponds to the probability of a molecule occupying a specific energy state. Since each independent roll follows the same probability distribution (e.g. 40% for 1, 30% for 2, 17% for 3 and 13% for 4), the likelihood of any outcome is the same for a single roll or for many rolls. Likewise, at equilibrium, the probability that a single molecule is in a given energy state is equal to the fraction of the total number of molecules in that state.
To elaborate on this concept, consider an equally spaced array of energy levels (0, ,
, …,
) like those of a harmonic oscillator, with
Let . Since
for
(see this article for details), eq252 and eq251 become
and
respectively, where .
Most diatomic molecules are in their vibrational ground state at room temperature. For example, if and
, the state populations (according to eq254) are
,
and
. At higher temperatures, e.g.
, more vibrational levels become populated, with
,
,
,
,
,
,
and
. These results are illustrated in the diagram below.
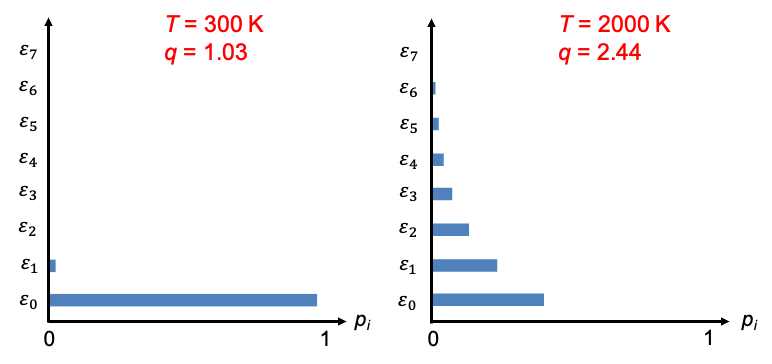
Notably, a higher value of corresponds to a larger number of significantly populated states. Therefore, the molecular partition function provides a measure of how many energy states are thermally accessible at a given temperature and, together with the Boltzmann distribution, partitions the total probability among the available energy levels.

Question
If the molecular partition function is related to the Boltzmann distribution, which is based on distinguishable particles, is it applicable to distinguishable or indistinguishable particles since it can also be used to describe a collection of particles?
Answer
The molecular partition function is defined for a single non-interacting molecule and does not itself assume distinguishability or indistinguishability. When extended to a system of non-interacting molecules, the probability that a molecule occupies a particular state remains , which is the same fraction of molecules in that state regardless of whether the molecules are considered distinguishable or indistinguishable. This is because each molecule independently follows the same single-particle probability distribution. The distinction between distinguishable and indistinguishable particles only affects the form of the canonical partition function
, not the calculation of these fractions.
The molecular partition function can also be expressed as:
where refers to the number of states having the same energy
(degenerate states), and the sum is now over degenerate states, not individual states.

Question
Use an example to show that eq250 and eq255 are equivalent.
Answer
|
Energy Level, |
Degeneracy, |
Contributing States |
|
0 |
2 |
A, B |
|
3 |
C, D, E |
|
| 1 |
F |
Using eq250,
Using eq255,
Finally, the total energy of a molecule in state can be approximated as:
where
is the translational energy of the molecule in state
is the rotational energy of the molecule in state
is the vibrational energy of the molecule in state
is the electronic energy of the molecule in state
The validity of eq256 is based on the following assumptions:
-
- The four types of energy are independent of each other. For instance, coupling between vibrational and rotational motion is small and can be neglected.
- The Born-Oppenheimer approximation is applied, which assumes that electronic motion can be treated independently of nuclear motion (translation, rotation, vibration) because electrons move much faster than nuclei. This results in the total wavefunction of the molecule being approximated as the product of four wavefunctions:
.
- Substituting eq256 into eq250 gives
Since the sum is over all states , we have
This factorisation of the molecular partition function is extremely useful in statistical mechanics because it allows us to treat each mode of motion — translational, rotational, vibrational, and electronic — independently. Instead of summing over all possible combinations of quantum states for the entire molecule (which can be computationally intractable), we can compute simpler, separate partition functions for each type of motion. This greatly simplifies calculations of thermodynamic properties such as internal energy, entropy and heat capacity. It also helps to explain the transition state theory.