Moments of inertia of a trigonal planar oblate symmetric rotor with $D_{3h}$ symmetry

The moments of inertia of a trigonal planar oblate rotor with $D_{3h}$ symmetry (e.g. BF₃) are characterised by a unique moment of inertia $I_{\parallel}$ around the principal axis and two equal moments of inertia $I_{\perp}$ perpendicular to the principal axis, where $I_{\parallel}>I_{\perp}$ . They are derived using simple geometric considerations.

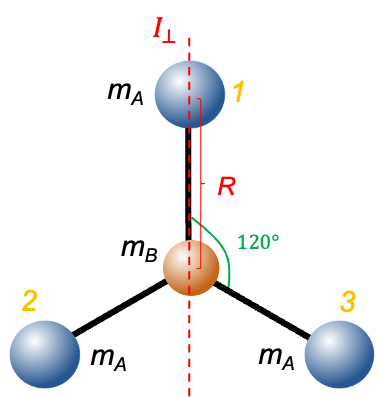
The diagram above shows a trigonal planar oblate rotor with its centre of mass located at atom B (of mass $m_B$ ), which is positioned at the origin $(0,0,0)$ . The three A atoms (1,2 and 3), each with mass $m_A$ , are equally spaced at 120° apart on an imaginary circle of radius $R$ .

The moment of inertia along the $z$ -axis, which is perpendicular to the plane of the diagram, is $I_{\parallel}=\sum_{i=1}^3m_ir_i^2=\sum_{i=1}^3m_i(x_i^2+y_i^2)$ . Since the three B-A bonds have equal lengths of $R$ , we have

$I_{\parallel}=3m_AR^2\;\;\;\;\;\;\;\;38$

Question

Why do $m_B$ not contribute to $I_{\parallel}$ ?

Answer

In general, $I_{\parallel}=\sum_{i=1}^Nm_ir_i^2=\sum_{i=1}^Nm_i(x_i^2+y_i^2+z_i^2)$ . Since atom B lie along the rotational axis, the moment of inertia about this axis is effectively zero due to the absence of perpendicular mass displacement ( $z_i=0$ ).

To derive $I_{\perp}$ , we can make use of the coordinates of the atoms that form the base of a trigonal pyramidal molecule mentioned in an earlier article, where $m_B=0$ and $\phi=90\degree$ :

Atom	Coordinates
Atom	Trigonal pyramidal	Trigonal planar
A₁	$\biggr$Rsin\phi,0,-\frac{m_BRcos\phi}{3m_A+m_B}\biggr$$	$(R,0,0)$
A₂	$\biggr$-\frac{1}{2}Rsin\phi,\frac{\sqrt{3}}{2}Rsin\phi,-\frac{m_BRcos\phi}{3m_A+m_B}\biggr$$	$\biggr$-\frac{1}{2}R,\frac{\sqrt{3}}{2}R,0\biggr$$
A₃	$\biggr$-\frac{1}{2}Rsin\phi,-\frac{\sqrt{3}}{2}Rsin\phi,-\frac{m_BRcos\phi}{3m_A+m_B}\biggr$$	$\biggr$-\frac{1}{2}R,-\frac{\sqrt{3}}{2}R,0\biggr$$