Moments of inertia of octahedral prolate symmetric rotor with \(D_{4h}\) symmetry

The moments of inertia of an octahedral prolate rotor with symmetry (e.g. Pt(NH₃) ₂Cl₄) are characterised by a unique moment of inertia around the principal axis and two equal moments of inertia perpendicular to the principal axis, where . They are derived using simple geometric considerations.

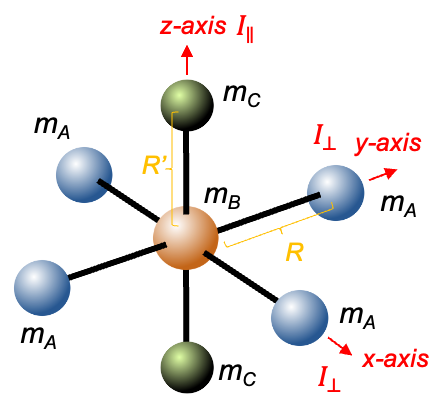
The diagram above shows an octahedral molecule of the type BA₄C₂, where B is the central atom. The moment of inertia along the -axis is . Since the four B-A bonds have equal lengths of , we have

 

 

Similarly, the moment of inertia of the molecule about the -axis, which is equal to that about the -axis, is . Since the two B-C bonds have equal lengths of , we have

You’ll find that the expression for the moment of inertia about the -axis is the same as eq36.

 

Next article: Moments of inertia of a trigonal planar oblate symmetric rotor with D_3h symmetry

Previous article: Moments of inertia of tetrahedral prolate symmetric rotor with C_3v symmetry

Content page of rotational spectroscopy

Content page of advanced chemistry

Main content page