A spherical rotor is a molecule in which the moments of inertia about all three principal axes are equal. This high degree of symmetry, typically found in molecules with tetrahedral (e.g. methane, CH₄), octahedral (e.g. sulfur hexafluoride, SF₆), or icosahedral geometries, leads to simplified rotational behaviour. Unlike asymmetric or symmetric rotors, spherical rotors exhibit degenerate energy levels due to their identical rotational constants along each axis. As a result, they serve as important models in quantum mechanics and spectroscopy, particularly for interpreting rotational spectra and understanding molecular symmetry.
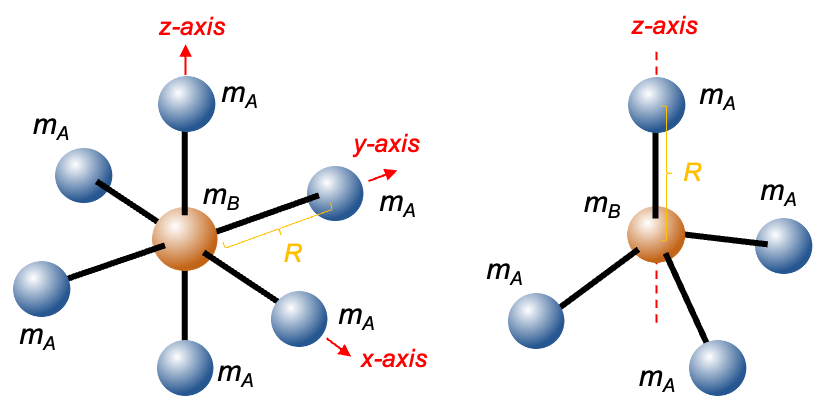
The left diagram above shows an octahedral molecule of the type BA6 ( symmetry), where B is the central atom. The moment of inertia along the
-axis, which is equal to those along the
-axis and
-axis, is
or

Question
Why do the three atoms that lie along the -axis not contribute to
?
Answer
In general, . Since the three atoms along the rotational axis, the moment of inertia about this axis is effectively zero due to the absence of perpendicular mass displacement (
).
To determine the moment of inertia of the tetrahedral molecule around the -axis, let atom B be at the centre of a cube (see diagram above), which is designated as the origin
. The four A atoms (
,
,
and
) are located at alternating vertices, with coordinates:
,
,
and
, where
is the half the length of an edge of the cube.
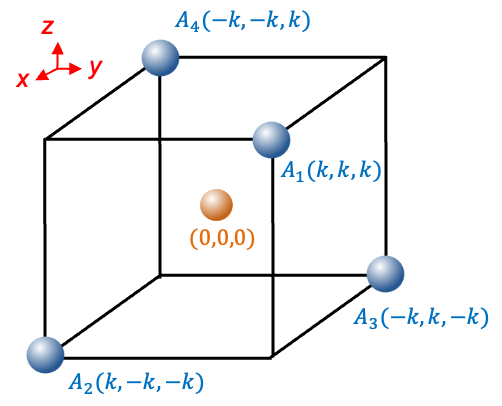
Since the B-A bond length is , we have
, which when substituted back into the coordinates yields:
,
,
and
. Therefore, the moment of inertia of the tetrahedral molecule around the
-axis is: