The moments of inertia of a tetrahedral prolate rotor with 
symmetry (e.g. CHCl3) are characterised by a unique moment of inertia 
around the principal axis and two equal moments of inertia 
perpendicular to the principal axis, where 
. They are derived using simple geometric considerations.
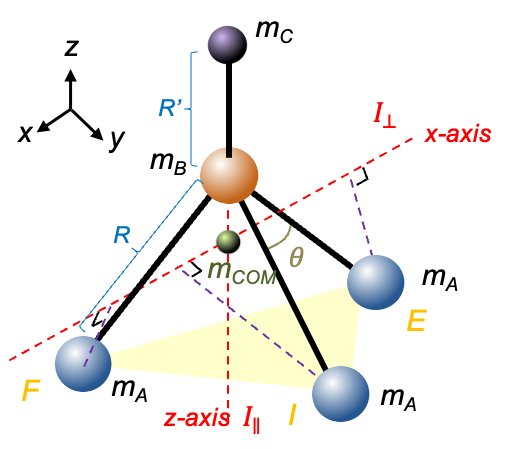
Since the rotation about the 
axis (
-axis) of the molecule has the same symmetry as a trigonal pyramidal molecule, the moment of inertia for symmetric rotors like CHCl3 along the -axis is given by eq22:
R^2)
To derive the expression for , place the origin at the centre of mass of the molecule. The -coordinates of atom C, atom B and each of the A atoms are 
, 
and 
respectively. Then, the centre of mass of the molecule satisfies +m_Bz_B+3m_A(z_B-Rcos\phi)=0)
or
with
Using the 
and 
coordinates of the three A atoms defined in the previous article, the positions of the atoms are:
| Atom |
Coordinates |
| C |
) |
| B |
) |
| A (point F) |
) |
| A (point I) |
) |
| A (point E) |
|
Since )
, the moment of inertia of the molecule about the -axis is )
. Substituting the data from the above table and eq23 into this equation gives:
+\frac{m_AR^2(1+2cos\theta)(m_B+m_C)}{3m_A+m_B+m_C}+\\&\frac{6m_Am_CR'R\sqrt{\frac{1}{3}(1+2cos\theta)}}{3m_A+m_B+m_C}+\frac{m_CR'^2(3m_A+m_B)}{3m_A+m_B+m_C}\;\;\;\;\;\;\;\;33\end{align})
You’ll find that substituting the data from the above table into the expression for the moment of inertia of the molecule about the -axis )
, and then substituting eq23 into the resultant equation, yields the same expression as eq33. Therefore, eq22 and eq33 represent two distinct moments of inertia of a tetrahedral prolate rotor with symmetry.
Question
Does eq33 apply to CH3Cl, where the centre of mass of the molecule is between C and Cl?
Answer
Yes it does. Eq33 applies to any tetrahedral prolate rotor with symmetry. You can convince yourself by deriving the expression using the geometry of CH3Cl.