Moments of inertia of triatomic linear molecules

The moments of inertia of triatomic linear molecules play a fundamental role in understanding their rotational dynamics and spectroscopic behaviour.

In such molecules — composed of three atoms aligned along a straight line — the distribution of mass relative to the molecular axis determines how the molecule responds to rotational motion. Since all atoms lie along the same axis, the moment of inertia about this axis is effectively zero due to the absence of perpendicular mass displacement. However, the moment of inertia about axes perpendicular to the molecular axis becomes significant and is central to characterising the molecule’s rotational energy levels.

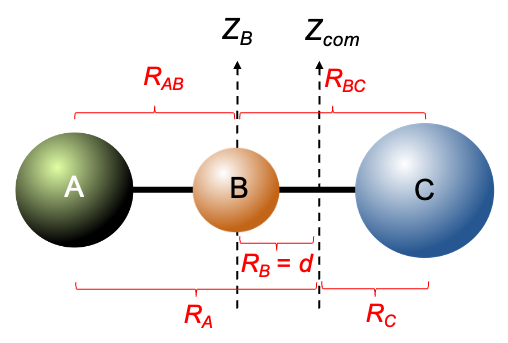
Consider a linear molecule with three atoms A, B and C with masses $m_A$ , $m_B$ and $m_C$ respectively, and bond lengths $R_{AB}$ and $R_{BC}$ (see diagram above). The molecule rotates the centre of mass axis $Z_{com}$ , which passes through the centre of mass of the molecule. If $R_A$ , $R_B$ and $R_C$ are the distances between the centre of mass and the respective atoms, then the parallel axis theorem states that:

$I_B=I_{com}+Md^2\;\;\;\;\;\;\;\;11$

where $I_B$ is the moment of inertia about the axis $Z_B$ , $I_{com}$ is the moment of inertia about the axis $Z_{com}$ , $M=\sum_{i=A}^Cm_i=m_A+m_B+m_C$ and $d=R_B$ .

Substituting $I_B=m_AR^2_{AB}+m_CR^2_{BC}$ in eq11 gives

$I_{com}=m_AR^2_{AB}+m_CR^2_{BC}-Md^2\;\;\;\;\;\;\;\;12$

Let’s assume that the molecular axis is the $x$ -axis with the origin at B. By definition, the center of mass with respect to the $x$ -coordinate satisfies $m_A(-R_{AB})+Md+m_CR_{BC}=0$ , which rearranges to: