A point group consists of geometric transformations known as symmetry operations, which preserve a single common point while transforming an object defined in a real vector space into physically indistinguishable replicas of itself.
Although an object undergoing a symmetry operation ends up looking the same after the transformation, the labelling of similar components of the object may change. In other words, to form a point group, all symmetry operations for an object must:
-
- Send the object into physically indistinguishable copies of itself.
- Combine with one another through binary operations such that the results are consistent with the 4 properties of a group.
- Leave one point invariant.
Point groups are determined by considering symmetry operations for different objects, beginning with simple shapes and moving on to more complex ones. According to the three abovementioned requirements, we start by inspecting the chosen object visually and finding all the symmetry elements (not to be confused with group elements) and their associated symmetry operations. For example, the only symmetry elements for the object in figure I, which is made up of two equally spaced right-angled triangles on a circle, are the identity symmetry element and a 2-fold rotation axis
. The corresponding symmetry operations are
and
.
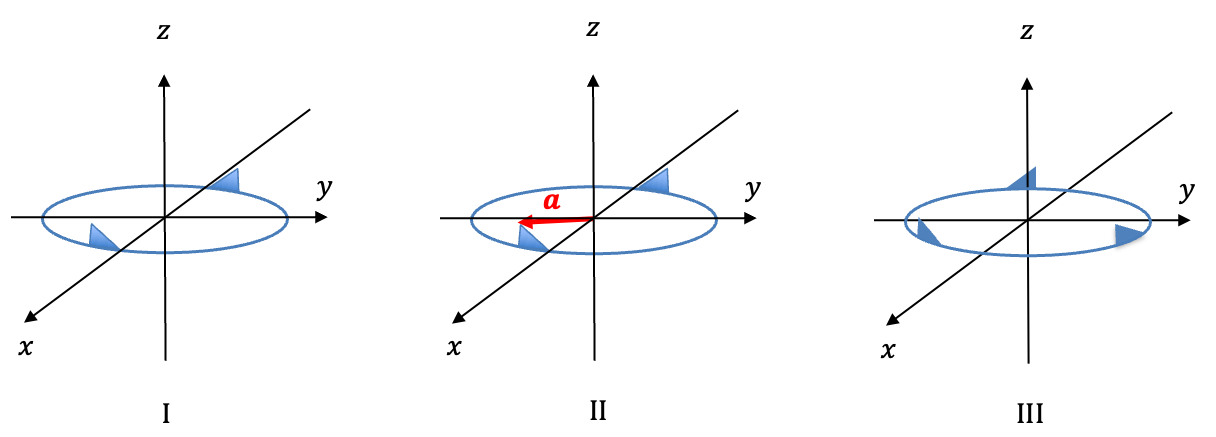
Next, we select a position vector (see figure II) and perform the symmetry operations
and
consecutively on the position vector. The results, in relation to the transformation of the position vector, are summarised in the multiplication table i:
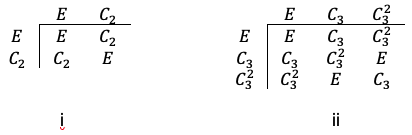
Note that we have omitted the carets – i.e. – for simplicity. From the table, we can easily verify all four properties of the group, e.g. the identity element is
and the inverse of an element of the group is the element itself. Therefore, the set of symmetry operations
for the object forms a point group of order 2 under the binary operation of multiplication. We call this group the
point group. Similarly, the set of symmetry operations
for the object in figure III forms the point group
of order 3 (see multiplication table ii). In general, we have an infinite number of uniaxial point groups
, each of which is called a cyclic group, whose elements are
. For a cyclic group where
is even, one of its elements is equivalent to the symmetry operation
.
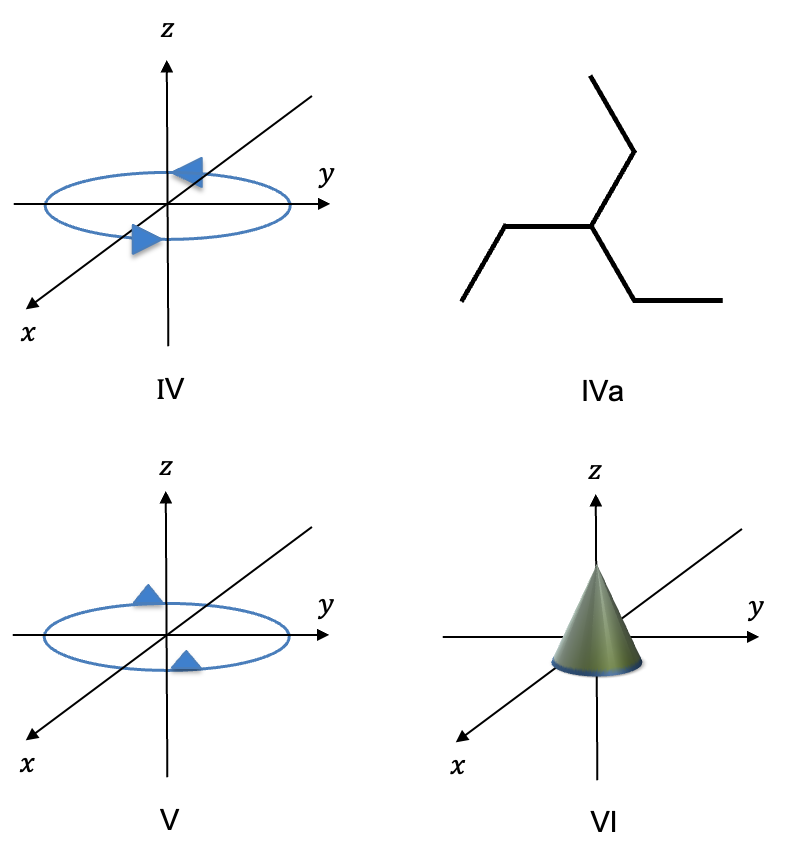
Let’s suppose the object in figure I have complete arrow heads (see figure IV). Other than and
, the object has a plane of symmetry perpendicular to the axis of rotation (the horizontal plane is denoted by
) and a centre of inversion
at the origin. The set of symmetry operations
forms the Abelian point group
(see multiplication table iii). The object in figure IVa belongs to the
point group (see multiplication table iv) with the set of elements
, where
. Similar to the
point groups, if we apply the same logic to other related objects, we have an infinite number of
point groups, each with symmetry operations of
if
is even (one of the
symmetry operations is equivalent to
) and
if
is odd.


Question
Why aren’t and
elements of the group
?
Answer
They are not unique elements, as they are equivalent to other ‘simpler’ elements of the group:
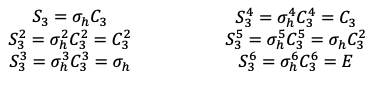
For an object that is made up of two equally spaced equilateral (or isosceles) triangles on a circle (see figure V above), we have the Abelian point group , whose elements are the symmetry operations
,
,
and
, where the symmetry elements for
and
are the vertical planes:
-plane and
-plane respectively. The multiplication table for this point group is shown in table v above. As before, we have an infinite number of
point groups. The cone depicted in figure VI is an example of an object that belongs to the
point group, where
, i.e. the
point group, with the set of symmetry operations:
.

Question
Are and
point groups?
Answer
is a trivial point group whose sole element is the symmetry operation
. An object of this group is considered to have no rotational symmetry.
and
have the same set of symmetry operations:
. Since objects of both point groups have no rotational symmetry, the symbol for the reflection symmetry operation does not have a subscript. In fact, these point groups are so unique that they are collectively known as the point group
(for Spiegel, the German word for mirror).
Another unique point group not mentioned above is , whose elements are the symmetry operations
and
.
and
are known as the non-axial point groups.
The next few related point groups are and
(for dihedral). They are related in the sense that they have in common the elements
and
, which serve as identifiers in categorising molecules by point groups.
|
Example |
|||
|
Symbol |
Object | Group elements |
Notes |
 |
The object is cyclohexane in its twisted boat form. A rhombic disphenoid (tetrahedron with scalene triangles as its faces) also belong to this point group. | ||
 |
|
||
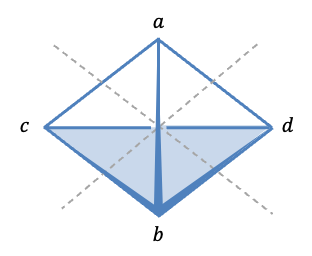 |
The object is a tetragonal disphenoid (faces are isosceles triangles). 1) 2) 3) |
||
The and
point groups are identical to the
and
point groups respectively in non-standard orientation, i.e. the principal axis is along the
-axis. A dumbbell has symmetry elements that are associated with the symmetry operations of
which is a special point group like .
Next, we have the point group, which is in general associated with the symmetry operations
. When
, we have the point group
, which is the same as the point group
. When
, the point group
is identical to the point group
. For
, we need to analyse the point group
with odd and even
separately.
Consider an point group
. When
is odd, the symmetry operation
. If
, then we have
or
(according to the closure property of a group). Since
, then
. Moreover,
, which implies that
. We can rewrite the symmetry operations of the
point group (
is odd) as
which is equivalent to the set of elements of the point group . For example, the object in figure IVa belongs to the point group
and hence to the point group
.
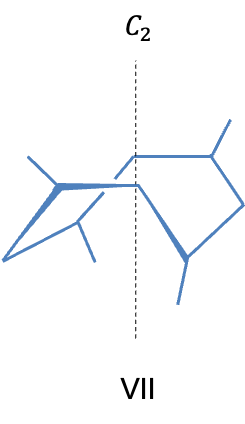
When is even, the symmetry operation
. Since
, we have
or
. Similarly,
or
. This implies that
. The elements of
can be denoted by
, where
can be odd or even. If
is even, then
. For example,
and
. If
is odd, then
. We can therefore express the symmetry operations for the
point group (when
is even) as
. Figure VII depicts an object that belongs to the
point group.
Taking into account the above characteristics of the point group, it is possible to relabel it as the
point group, where
.
The rest of the point groups are the tetrahedral groups , the octahedral groups
, the icosahedral groups
and the special orthogonal group in 3-dimensions
(also known as the full rotation group). The tetrahedral and octahedral groups are collectively called the cubic groups.
| Symbol | Object | Group elements | Notes |
 |
Each of the three |
||
 |
or simply |
Same rotation axes as |
|
 |
Same rotation axes as |
||
 |
or simply |
Same as |
|
 |
Same as |
||
 |
The object is a snub dodecahedron with 92 faces (12 pentagons, 80 equilateral triangles), 150 edges and 60 vertices. | ||
 |
The object is a truncated icosahedron with 32 faces (12 pentagons, 20 hexagons), 90 edges and 60 vertices. Same symmetry elements as |
||
 |
The object is a sphere with an infinite number of rotation axes, each with all possible values of |

Question
Why are and
called tetrahedral point group and octahedral point group respectively?
Answer
A regular tetrahedron and a regular octahedron have all the same symmetry elements as those used to derive the point group and the
point group respectively. A tetrahedron with reduced symmetry (e.g. with figure IVa attached to its faces) belongs to the
point group. Similarly, an octahedron with attachments to its vertices belong to the
point group.