
Question 1
Show that the triple hexagonal lattice (Vc) becomes a cubic P lattice when the perpendicular distance between two layer of lattices, h, is(IaI√6)/6.
Answer 1
The diagram below shows two layers of the triple hexagonal lattice Vc.
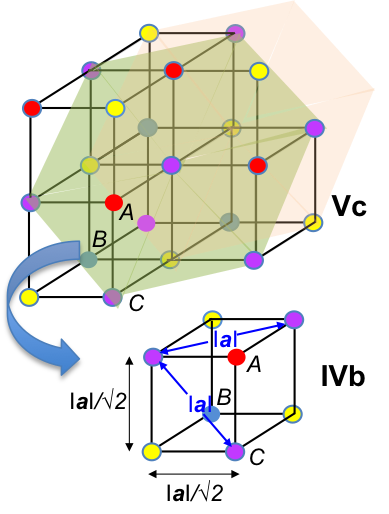
Focusing on just one segment of the space lattice (IVb), IaI refers to the separation between two same-layer lattice points of Vc and is also the surface diagonal of IVb. The body diagonal AB of IVb is determined using Pythagoras’ theorem as follows:
Each side of the cubic P unit cell is IaI/√2 and
Furthermore, AB is thrice the perpendicular distance between two layers of the triple hexagonal lattice Vc (see below diagram, which is IVb rotated for a better view).
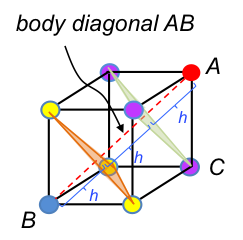
Since AB = 3h,

Question 2
Show that the triple hexagonal lattice (Vc) becomes a cubic F lattice when the perpendicular distance between two layer of lattices, h, is(IaI√6)/3.
Answer 2
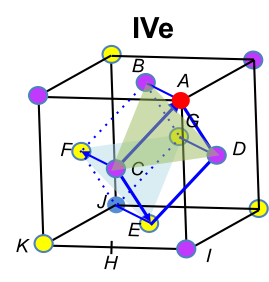
Similar to the cubic P unit cell, IaI refers to the separation between two same-layer lattice points of Vc in the cubic F unit cell, e.g. the length of BC. Using Pythagoras’ theorem,
By the symmetry of the cubic F unit cell, BC = CE = IaI and CH = HE. Therefore, CH = IaI/√2 and hence, AI = 2IaI/√2. Furthermore,
Since (IJ)2 = (KI)2 + (KJ)2 = (AI)2 + (AI)2 = 2(AI)2 = 4IaI2,
Just like the cubic P unit cell, the body diagonal AJ of the cubic F unit cell (IVe) is thrice the perpendicular distance between two layers of Vc. Therefore,
