Quantum tunnelling is a phenomenon in which a particle passes through a potential energy barrier that it classically does not have enough energy to overcome.
In classical terms, a ball rolling up a hill without enough energy to reach the top would simply roll back down. However, in the quantum world, particles such as electrons are described by wavefunctions that represent probabilities of where they might be found. Because these wavefunctions extend slightly into and beyond barriers, there is a finite probability that the particle will appear on the other side, as though it has “tunnelled” through.
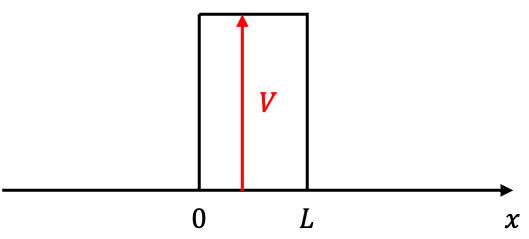
Consider a particle in the potential energy regions shown in the diagram above, where
where is a finite potential energy value.
The Schrödinger equation for the regions and
is
, while that for
is
. It follows that the general solutions (which can be verified by substituted them into the respective Schrödinger equations) are:
where and
, with
.

Question
Show that and
are eigenfunctions of the linear momentum operator
, and interpret the eigenvalues with regard to the motion of a particle.
Answer
and
. Since the two wavefunctions are associated with momentum eigenvalues of equal magnitude but opposite signs,
represents a particle travelling in the positive
-direction with momentum
, while
represents a particle travelling in the negative
-direction with momentum
.
Therefore, is the complete wavefunction of the particle moving towards the barrier from the left, consisting of an incident wave and a reflected wave from the barrier. If the particle is able to penetrate the barrier, it can only move to the right of the barrier, which implies that
.
For ,
and
to be acceptable solutions to their respective Schrödinger equations, they must be continuous at the boundaries of the potential regions (at
and
), and their first derivatives must also be continuous. Specifically, this requires:
1) and
or
2) and
or
To solve the four simultaneous equations, we begin by substituting eq2 into eq4 to give
and
Solving eq5 and eq6 yields:
and
Substituting eq1 into eq3 results in , or equivalently:
Substituting eq7 and eq8 into eq9 and rearranging gives
Since, , or equivalently
, eq10 becomes
Expanding the denominator of eq11 and simplifying yields:
The probability that the particle is travelling in the positive -direction towards the left of the barrier is
, while the probability of it travelling in the same direction on the right of the barrier is
. Therefore, the ratio
represents the transmission probability
.
Multiplying eq12 with its complex conjugate, and using the identities and
, yields:
which rearranges to:
Substituting and
into eq13 and simplifying results in:
where .
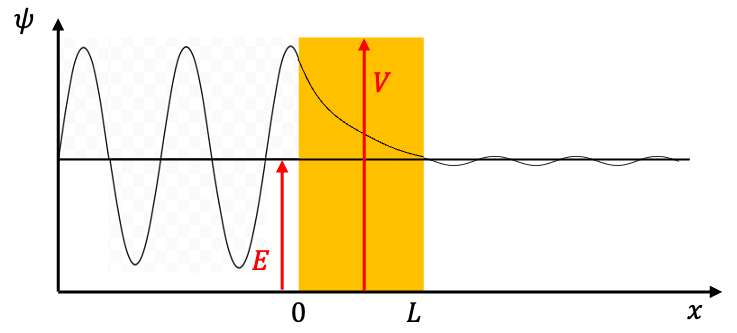
For high potential and wide barriers, where , eq14 simplifies to:
Since , the transmission probability decreases exponentially with the thickness of the barrier
(see diagram above) and with
when
. In other words, lighter particles are more likely to tunnel through barriers than heavier ones. For example, electrons can tunnel efficiently through a few nanometres of GaAs semiconductor with a barrier potential of V ∼ 0.1 − 1 eV, or through 0.5 − 1 nm of vacuum with a barrier potential of V ∼ 4 − 5 eV in scanning tunnelling microscopy (STM).

Question
Why is in the region
depicted as a standing wave in the above diagram?
Answer
is depicted as a standing wave for simplicity. When the transmission probability is small,
, and
is the condition for a perfect standing wave. In reality, it represents a partial standing wave, since the amplitudes are not exactly equal.
In conclusion, quantum tunnelling has profound implications across physics, chemistry, and technology. It explains how nuclear fusion occurs in stars, where protons can tunnel through repulsive energy barriers despite not having enough kinetic energy to overcome them. In modern technology, tunnelling is exploited in devices such as tunnel diodes and scanning tunnelling microscopes, which can image surfaces at the atomic level. It also plays a role in radioactive decay and quantum computing, where tunnelling effects can influence qubit stability and transitions. Overall, quantum tunnelling is a cornerstone of quantum theory and a striking demonstration of how the microscopic world defies classical intuition.