Radioactive decay is the spontaneous process by which an unstable atomic nucleus transforms into a more stable one by emitting particles or energy.
It follows first-order kinetics, meaning the rate at which a radioactive nucleus transforms is directly proportional to the number of un-decayed nuclei at any given time . Because each nucleus decays independently, the probability that a nucleus will decay in a small interval of time is constant, regardless of how long the atom has existed. Mathematically, the rate law is given by:
where , the decay constant, represents the probability of decay per unit time.
An example of radioactive decay is the transformation of uranium-238 into thorium-234 with the emission of an alpha particle (a helium nucleus):
Thorium-234, which is also radioactive, then undergoes beta decay (a beta particle is an electron) to produce protactinium-234, and continues through a chain until a stable lead-206 nucleus is formed:
Question
Why does a radioactive nucleus have a constant probability of decaying in any given interval of time?
Answer
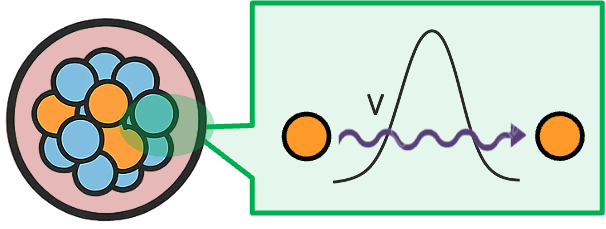
In uranium-238, the alpha particle is held inside the nucleus but is surrounded by a repulsive electrostatic barrier created by the positively charged protons. Classically, the alpha particle does not have enough energy to overcome this barrier potential
. However, quantum mechanics allows a finite probability for the particle to penetrate the barrier through a phenomenon called quantum tunnelling (see diagram below). The tunnelling (or transmission) probability depends on the particle’s mass, the ratio
and the width of the barrier. Because these quantities are fixed for a given isotope, the probability that a nucleus will decay in a small interval of time remains constant, leading to the characteristic constant decay probability per unit time observed in radioactive decay.
Solving eq60 by integration gives:
where is the number of un-decayed nuclei at
.
Therefore, the probabilistic decay behaviour leads to an exponential decrease in the number of radioactive nuclei as time passes.
For a first order reaction, the half life is constant and given by:
Because is specific to each radioactive isotope, every radionuclide has a characteristic half-life, which can be exploited to gain insight into the age of a material. For example, the analysis of radioactive elements within meteorites allow scientists to estimate the age of the earth. One commonly used method involves the decay of uranium-238 to lead-206. Uranium-238 has a half-life of about 4.47 billion years, meaning that after this time, half of the original 238U atoms in a sample will have decayed to 206Pb. By measuring the present-day ratio of parent isotope (238U) to daughter isotope (206Pb) in ancient minerals, such as zircon crystals found in some of the oldest meteorites, scientists can determine how many half-lives have elapsed.
Question
1) If 238U actually decays to 234Th, why is the half-life stated as 4.47 billion years from 238U to 206Pb?
2) How is the ratio of parent isotope to daughter isotope measured?
Answer
1) The half-life for the decay of 238U to 234Th is about 4.47 billion years. All the subsequent steps in the decay chain leading to 206Pb have very short half-lives, from minutes to tens of thousands of years, expect 234U, which has a half-life of 245,500 years. Therefore, the cumulative time from 238U to 206Pb is still about 4.47 billion years.
2) The ratio of isotopes is measured using thermal ionisation mass spectrometry (TIMS). In this technique, the zircon sample is dissolved in acid, and the resultant solution is heated to produce ions, which are then accelerated into the spectrometer. The TIMS detector measures the resulting ion current, which is proportional to the number of ions striking it. By slightly adjusting the magnetic field, each isotope can be measured sequentially. Although the ion currents are extremely small, often only a few picoamperes, TIMS electronics integrate the signal over time to achieve very high precision, allowing isotope ratios to be determined with accuracy better than 0.01%.
Suppose zircon samples from the oldest meteorite on Earth are measured by TIMS to have values very close to:
From eq61, the number of 238U atoms remaining at time is:
Zircon (ZrSiO4), during its initial formation, incorporates U4+ easily but not Pb2+ because U⁴⁺ closely matches Zr4+ in both charge and ionic radius, allowing it to substitute easily, whereas Pb²⁺ has a lower charge and a much larger radius, making substitution energetically unfavourable. Therefore, lead is typically below detection levels initially, and the number of 206Pb atoms formed is:
It follows that the uranium-to-lead ratio can be expressed as:
Solving for yields:
Substituting eq62, where billion years, into eq64 gives
billion years. Since
represents the time required for the original 238U to produce the measured uranium-to-lead ratio of 0.99, the earth is therefore approximately 4.5 billion years old.
